Молекулярно-кинетическая теория

Идеальных газов

Молекулярно-кинетическая теория описывает поведение и свойства особого идеального объекта, называемого ² идеальным газом ². В основе данной физической модели лежит молекулярное строение вещества. Создание молекулярной теории связано с работами Р. Клаузиуса, Дж. Максвелла, Д. Джоуля и Л. Больцмана.

Идеальный газ. Молекулярно-кинетическая теория идеального газастроится на следующих посылках:

1) атомы и молекулы можно рассматривать как материальные точки, находящиеся в непрерывном движении;

2) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;

3) все атомы и молекулы являются различимыми, то есть существует принципиальная возможность следить за движением каждой частицы;

4) до столкновения молекул газа между ними отсутствуют силы взаимодействия, а соударения молекул между собой и со стенками сосуда предполагаются абсолютно упругими;

5) движение каждого атома или молекулы газа описывается законами классической механики.

Законы, полученные для идеального газа можно использовать при изучении реальных газов. Для этого создают экспериментальные модели идеального газа, в которых свойства реального газа близки характеристикам идеального газа (например, при низких давлениях и высоких температурах).

Законы идеального газа

Закон Бойля-Мариотта:

для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная: рV = const, (1.1)

при T = const, m = const.

Кривая, изображающая зависимость между величинами р и V, характеризует свойства вещества при постоянной температуре, и называется изотермой - это гипербола (рис.1.1.), а процесс, протекающий при постоянной температуре, называется изотермическим.

Законы Гей-Люссака:

1. Объем данной массы газа при постоянном давлении изменяется линейнос температурой

V = V ₀(1 + a ×t) при Р = const, m = const. (1.2)

2.
Давление данной массы газа при постоянном объеме изменяется линейно с температурой (закон Шарля):

p = p ₀ (1 + a× t) при V = const, m = const. (1.3)

В уравнениях (1.2) и (1.3) температура выражена по шкале Цельсия, давление и объем – при0 °С, при этом .

 

Процесс, протекающий при постоянном давлении, называется изобарным, его можно представить в виде линейной функции(рис. 1.2.).

Процесс, протекающий при постоянном объеме, называется изохорным (рис. 1.3.).

Из уравнений (1.2) и (1.3) следует, что изобары и изохоры пересекают ось температур в точке t = -1/a= - 273,15 °С. Если перенести начало отсчета в эту точку, то перейдем к шкале Кельвина.

Вводя в формулы (1.2) и (1.3)термодинамическую температуру, законам Гей-Люссака можно придать более удобный вид:

V = V ₀ (1+a t) = = V ₀ [1+ a(T -1/a)] = = V ₀ a T;

p = p ₀ (1+a t) = p ₀ [1+ a(T -1/a)] = p ₀ a T;

при p = const, m = const; (1.4)

при V = const, m = const, (1.5)

где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.

Закон Авогадро:

моли любых газов при одних и тех же температурах и давлениях занимают одинаковые объемы.

При нормальных условиях этот объем равен V _m,0 = 22,41×10^-3 м³/моль. По определению, в одном моле различных веществ содержится одно и то же число молекул, равное постоянной Авогадро: N_A = 6,022×10²³моль^-1.

Закон Дальтона:

давление смеси разных идеальных газов равно сумме парциальных давлений р ₁, р ₂, р ₃ … р _n, входящих в нее газов:

р = р ₁ + р ₂ + р ₃ + …+ р_n.

Парциальное давление – этодавление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.

Уравнение состояния идеального газа

(уравнение Клапейрона-Менделеева)

Между температурой, объемом и давлением существует определенная связь. Эта связь может быть представлена функциональной зависимостью:

f (p, V, T) = 0.

В свою очередь каждая из переменных (р, V, T) является функцией двух других переменных. Вид функциональной зависимости для каждого фазового состояния вещества (твердого, жидкого, газообразного) отыскивается экспериментально. Это весьма трудоемкий процесс и уравнение состояния установлено лишь для газов, которые находятся в разреженном состоянии, и в приближенной форме – для некоторых сжатых газов. Для веществ, находящихся не в газообразном состоянии, эта задача до сих пор не решена.

Французский физик Б. Клапейрон вывел уравнение состояния идеального газа, объединив законы Бойля-Мариотта, Гей-Люссака, Шарля:

. (1.6)

Выражение (1.6) и есть уравнение Клапейрона, где В – газовая постоянная. Она различна для разных газов.

Д.И. Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (1.6) к одному молю и использовав молярный объем V _m. Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем V _{m .}. Поэтому постоянная В будет одинаковой для всех идеальных газов. Данная постоянная обычно обозначается R и равна R = 8,31 .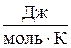

Уравнение Клапейрона-Менделеева имеет следующий вид:

p V _m. = R T.

От уравнения (1.7) для одного моля газа можно перейти к уравнению Клапейрона-Менделеева для произвольной массы газа:

, (1.7)

гдеm – молярная масса(масса одного моля вещества, кг/ моль); m -масса газа; - количество вещества.

Чаще пользуются другой формой уравнения состояния идеального газа, вводя постоянную Больцмана: .

Тогда уравнение (1.7) выглядит так:

, (1.8)

где – концентрация молекул (число молекул в единице объема). Из этого выражения следует, что давление идеального газа прямо пропорционально концентрации его молекул или плотности газа. При одних и тех же температурах и давлениях все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м³ при нормальных условиях, называется числом Лошмидта:

N_L = 2,68× 10²⁵ м^-3.

Основное уравнение молекулярно-кинетической

теории идеальных газов

Важнейшей задачейкинетической теории газовявляется теоретический расчет давления идеального газана основе молекулярно-кинетических представлений.Основное уравнение молекулярно-кинетической теории идеальных газов выводится с использованием статистических методов.

Предполагается, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, и эти соударения абсолютно упругие. На стенке сосуда выделяют некоторую элементарную площадку D S и вычисляют давление, которое будут оказывать молекулы газа на эту площадку.

Необходимо учитывать то, что реально молекулы могут двигаться к площадке под разными углами и могут иметь различные скорости, которые к тому же при каждом соударении могут меняться. В теоретических расчетах хаотические движения молекул идеализируется, их заменяют движением вдоль трех взаимно перпендикулярных направлений.

Если рассмотреть сосуд в виде куба, в котором беспорядочно движется N молекул газа в шести направлениях, то несложно заметить, что в любой момент времени вдоль каждого из них движется 1/3 количества всех молекул, причем половина из них (то есть. 1/6 количества всех молекул) движется в одну сторону, а вторая половина (тоже 1/6) - в противоположную. При каждом соударении отдельная молекула, движущаяся перпендикулярно площадке, отражаясь, передает ей импульс, при этом ее количество движения (импульс) меняется на величину

D Р ₁= m ₀ v – (– m ₀ v) = 2 m ₀ v.

Число ударов молекул, движущихся в заданном направлении, о площадку будет равно: N = 1/6 n D Sv D t. При столкновении с площадкой эти молекулы передадут ей импульс

D P = N ×D P ₁ =2 m ₀ v n D S v D t= m₀ v ² n D S D t,

где n – концентрация молекул. Тогда давление, которое газ оказываетна стенку сосуда, будет равно:

р = = n m ₀ v ². (1.9)

Однако молекулы газа движутся с различными скоростями: v ₁, v ₂, …, v_n, поэтому скорости необходимо усреднить. Сумма квадратов скоростей движения молекул газа, делённая на их количество, определяет среднеквадратичную скорость:

.

Уравнение (1.9)примет вид:

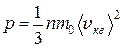(1.10)

выражение (1.10) называется основным уравнением молекулярно-кинетической теории идеальных газов.

Учитывая, что , получим:

р V = 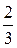N = 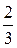Е, (1.11)

где Е – суммарная кинетическая энергия поступательного движения всех молекул газа. Следовательно, давление газа прямо пропорционально кинетической энергии поступательного движения молекул газа.

Для одного моля газа m = m, и уравнение Клапейрона-Менделеева имеет следующий вид:

p V _{m .} = R T,

и так как из (1.11) следует, что p V _{m .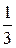} = má v _кв ñ ² , получим:

RT = 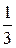má v _кв ñ ².

Отсюда средняя квадратичная скорость молекул газа равна

á v _кв ñ = = = ,

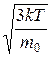где k = R / N_A = 1,38×10^-23 Дж/К –постоянная Больцмана. Отсюда можно найти среднюю квадратичную скорость молекул кислорода при комнатной температуре – 480 м/с, водорода – 1900 м/с.

Молекулярно-кинетический смысл температуры

Температура является количественной мерой «нагретости» тела. Для выяснения физического смысла абсолютной термодинамической температуры Т сопоставим основное уравнение молекулярно-кинетической теории газов (1.14) с уравнением Клапейрона-Менделеева p V = n R T.

Приравняв правые части этих уравнений, найдем среднее значение кинетической энергии e₀ одной молекулы (n = N / N_A, k = R / N_A):

.

Из этого уравнения следует важнейший вывод молекулярно-кинетической теории: средняя кинетическая энергия поступательного движения одной молекулы идеального газа зависит только от температуры, при этом она прямо пропорциональна термодинамической температуре. Таким образом, термодинамическая шкала температур приобретает непосредственный физический смысл: при Т = 0 кинетическая энергия молекул идеального газа равна нулю. Следовательно, исходя из этой теории, поступательное движение молекул газа прекратится и его давление станет равным нулю.

Теория равновесных свойств идеального газа

Число степеней свободы молекул. Молекулярно-кинетическая теория идеальных газов приводит к весьма важному следствию: молекулы газа совершают беспорядочное движение, причем средняя кинетическая энергия поступательного движения молекулы определяется исключительно температурой.

Кинетическая энергия движения молекул не исчерпывается кинетической энергией поступательного движения: она также складывается из кинетических энергий вращения и колебания молекул. Для того, чтобы подсчитать энергию, идущую на все виды движения молекул, необходимо дать определение числу степеней свободы.

Под числом степеней свободы (i) тела подразумевается число независимых координат, которые необходимо ввести для определения положения тела в пространстве.

Например, материальная точка обладает тремя степенями свободы, так как ее положение в пространстве определяется тремя координатами: х, у и z. Следовательно, одноатомная молекула обладает тремя степенями свободы поступательного движения.

Двухатомная молекула имеет 5 степеней свободы (рис. 1.4): 3 степени свободы поступательного движения и 2 степени свободы вращательного движения.

Молекулы из трех и более атомов имеют 6 степеней свободы: 3 степени свободы поступательного движения и 3 степени свободы вращательного движения (рис. 1.5).

Каждая молекула газа обладает определенным числом степеней свободы, три из которых соответствуют ее поступательному движению.

 

Положение о равнораспределении энергии

по степеням свободы

Основной предпосылкой молекулярно-кинетической теории газов является предположение о полной беспорядочности движения молекул. Это относится и к колебательному, и к вращательному движениям, а не только поступательному. Считается, что все направления движения молекул в газе равновероятны. Поэтому можно предположить, что на каждую степень свободы молекулы в среднем приходится одно и то же количество энергии – это есть положение о равнораспределении энергии по степеням свободы. Энергия, приходящаяся на одну степень свободы молекулы, равна:

. (1.12)

Если молекула обладает i степенями свободы, то на каждую степень свободы приходится в среднем:

. (1.13)

Внутренняя энергия идеального газа

Если отнести полный запас внутренней энергии газа к одному молю, то получим ее значение, умножив áeñ на число Авогадро:

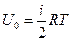. (1.14)

Отсюда следует, что внутренняя энергия одного моля идеального газа зависит только от температуры и числа степеней свободы молекул газа.

распределения Максвелла и Больцмана

Распределение молекул идеального газа по скоростям и энергиям теплового движения (распределение Максвелла). При постоянной температуре газа все направления движения молекул предполагаются равновероятными. В этом случае средняя квадратичная скорость каждой молекулы остаётся постоянной и равна

.

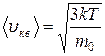Это объясняется тем, что в идеальном газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям. это распределение подчиняется определенному статистическому закону, который теоретически вывел Дж. Максвелл. Закон Максвелла описывается функцией

,

то есть функция f (v) определяет относительное число молекул , скорости которых лежат в интервале от v до v + dv. Применяя методы теории вероятностей, Максвелл нашел закон распределения молекул идеального газа по скоростям:

. (1.15)

Функция распределения в графическом виде представлена на рис. 1.6. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это значит, что функция f (v) удовлетворяет условию нормировки:

.

Скорость, при которой функция распределения молекул идеального газа по скоростям f (v) максимальна, называется наиболее вероятной скоростью v_B.

Значения v = 0и v = ¥соответствуют минимумам выражения (1.15). Наиболее вероятную скорость можно найти, продифференцировав выражение (1.23) и приравняв его к нулю:

= = 1,41

При увеличении температуры максимум функции сместится вправо (рис.1.6), то есть при увеличении температуры увеличивается и наиболее вероятная скорость, однако, ограниченная кривой площадь остаётся неизменной. Следует заметить, что в газах и при небольших температурах всегда присутствует небольшое количество молекул, которые движутся с большими скоростями. Наличие таких «горячих» молекул имеет большое значение при протекании многих процессов.

Средняя арифметическая скорость молекулы определяется по формуле

.

 

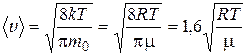Средняя квадратичная скорость

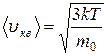= 1,73 .

Отношение этих скоростей не зависит ни от температуры, ни от вида газа.

Функция распределения молекул по энергиям теплового движения. Эту функцию можно получить, подставив в уравнение распределения молекул (1.15) вместо скорости значение кинетической энергии:

.

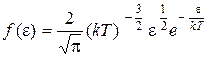Проинтегрировав выражение по значениям энергии от до 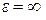, получим среднюю кинетическую энергию молекулы идеального газа:

.

Барометрическая формула. Распределение Больцмана. При выводе основного уравнения молекулярно-кинетической теории газов и распределения Максвелла молекул по скоростям предполагалось, что на молекулы идеального газа не действуют внешние силы, поэтому молекулы равномерно распределены по всему объему. Однако молекулы любого газа находятся в поле тяготения Земли. При выводе закона зависимости давления от высоты, предполагается, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова:

. (1.16)

Выражение (1.16) называется барометрической формулой. Оно позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, можно найти высоту. Так как h₁ – это высота над уровнем моря, где давление считается нормальным, то выражение можно модифицировать:

.

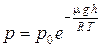Барометрическую формулу можно преобразовать, если воспользоваться выражением р = nkT:

,

где n – концентрация молекул на высоте h, m ₀ gh = П – потенциальная энергия молекулы в поле тяготения. При постоянной температуре плотность газа больше там, где меньше потенциальная энергия молекулы. Графически закон убывания числа частиц в единице объема с высотой выглядит, как показано на рис. 1.7.

Для произвольного внешнего потенциального поля запишем следующее общее выражение

,

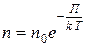которое называетсяраспределением Больцмана .

Лабораторная работа

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: