 |
Определение универсальной газовой постоянной
|
|
|
|
Цель работы: экспериментально определить универсальную газовую постоянную методом откачки.
Методика эксперимента
Универсальную газовую постоянную R можно определить из уравнения (1.7) Менделеева-Клапейрона
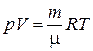, (1.26)
где p – давление; V – объём; m – масса; m – молярная масса газа.
Рассматривая уравнение (1.26) для двух масс m 1 и m 2 одного и того же газа при одинаковых температурах T и объёме V, получим выражения для универсальной газовой постоянной:
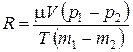. (1.27)
Если определить давление p 1 и температуру Т для некоторой массы газа m 1, заключенной в сосуде объёмом V, а затем изменить массу газа до m 2 (например, откачав газ) и вновь определить давление оставшегося газа p 2, то по формуле (1.27) можно рассчитать универсальную газовую постоянную R.
Начальную массу газа m 1 можно вычислить по формуле
m 1 = r V,
где r – плотность; V – объём газа.
Масса откачанного газа m 2 = r V 0,
где V 0 – объем откачанного газа.
Тогда масса оставшегося газа в сосуде
m 1 – m 2 = r(V – V 0).
Подставляя последнее выражение в уравнение (1.27), получим:
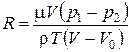. (1.28)
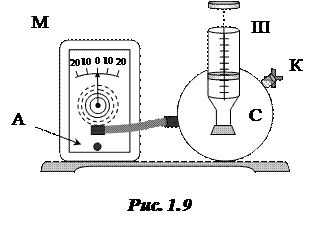Эксперимент выполняется на установке (рис. 1.9), состоящей из сосуда С (полый металлический цилиндр), имеющего три вывода. Один вывод соединен со шприцем Ш, второй – с микроманометром М, а в третий впаян кран К, сообщающий сосуд с атмосферой. Перемещая поршень шприца, можно откачать из сосуда С некоторый объем V 0 воздуха, меняя массу и давление воздуха в нем. Изменение давления в сосуде С фиксируется микроманометром, шкала которого проградуирована в миллиметрах водного столба.
Порядок выполнения работы
1. Открыв кран К, поставить поршень в шприце в начальное (нулевое) положение. кран закрыть.
2. Арретиром А микроманометра установить стрелку в нулевое положение.
|
|
|
3. Перемещая поршень в шприце, откачать из сосуда С воздух. Объём откаченного воздуха V 0 записать в таблицу 1.2.
4. Определить по микроманометру давление р 2, записать в таблицу.
5. Повторить три раза п. 1 – 4.
6. Записать в таблицу показания термометра (температура воздуха в лаборатории - Т) и барометра (атмосферное давление - p 1).
Таблица 1.2
| V 0, см3 | p 2, мм вод.ст. | Параметры | постоянные | R | 
|
| p 1 = мм.рт.ст p 1 = Па Т = К | m = 29×10-3 кг/моль r = 1, 293 кг/м3 1 мм рт.ст.=133,3 Па 1 мм вод.ст. =9,81 Па | ||||
Обработка результатов измерений
1. По формуле (1.28) вычислить универсальную газовую постоянную для
каждого эксперимента, переведя все входящие в нее величины в СИ.
2. Рассчитать среднее значение универсальной газовой постоянной .
3. Сравнить полученное значение универсальной газовой постоянной с табличным. Сделать вывод по проделанной работе.
Контрольные вопросы и задания
1. Какой физический смысл имеет универсальная газовая постоянная R? (используйте первое начало термодинамики для изобарического и изохорического процессов и формулу Майера)
2. Укажите единицы измерения универсальной газовой постоянной R в СИ.
3. Запишите основное уравнение молекулярно-кинетической теории идеальных газов (МКТ) и выведите из него уравнение Клапейрона-Менделеева.
4. Поясните метод определения универсальной газовой постоянной R в данной работе.
2. Явления переноса в термодинамически
Неравновесных системах
Виды процессов переноса
В предыдущих главах мы рассматривали исключительно равновесные свойства вещества или термодинамические процессы, которые квазистатически (то есть очень медленно) переводят систему из одного равновесного состояния в другое. Мы не рассматривали сами процессы перехода из одного состояния системы в другое. В изолированной макроскопической системе равновесное состояние характеризуется однородным распределением плотности (концентрации) вещества, температуры и отсутствием упорядоченного движения газа или жидкости. Система с неоднородным распределением параметров (плотности, температуры и т.д.) будет стремиться к равновесию, то есть к состоянию, характеризующемуся неизменностью этих параметров во времени и отсутствием в нем потоков (упорядоченного движения молекул газа или жидкости). Этот процесс называется релаксацией. Процессы выравнивания сопровождаются переносом ряда физических величин (массы, импульса, энергии) и называются потому явлениями переноса. скорость приближения неравновесной системы к равновесию должна быть связана с градиентами соответствующих параметров состояния 1. Эксперимент подтверждает это положение, которое позволяет описать явления диффузии (выравнивание плотности или концентрации за счет переноса массы в объеме), теплопроводности (выравнивание температуры по объему в результате переноса тепловой энергии хаотического движения частиц) и вязкости (выравнивание скоростей движения различных слоев текучей среды в связи с переносом импульса частиц сплошной среды).
|
|
|
1 Если некоторая скалярная величина А распределена в пространстве неравномерно, то быстроту (скорость) изменения этой величины по выбранному направлению характеризует градиент.
Градиент величины А (
) – вектор, направленный в каждой точке пространства в сторону быстрейшего возрастания этой величины, и численно равный изменению А на единицу длины этого направления. Если величина А меняется только вдоль одного направления (Оx), то модуль градиента:
.
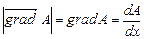За время dt через площадку, перпендикулярную к направлению переноса (х) будет перенесена некоторая физическая величина dB (масса, импульс, энергия), определяемая уравнением:
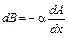dS ^× dt,
где a - коэффициент пропорциональности, называемый коэффициентом переноса. Знак ²-² означает, что направление возрастания величины А и направление переноса величины В противоположны, то есть перенос всегда происходит в сторону убыли величины А.
Законы переноса массы, энергии и импульса положены в основу теории неравновесных процессов, или физической кинетики. Прежде чем ознакомиться с законами физической кинетики, введем кинематические характеристики с помощью которых описывается движение молекул в среде.
|
|
|
Число столкновений и
средняя длина свободного пробега молекул
Молекулы газа, находясь в непрерывном хаотическом движении, сталкиваются друг с другом. Каково же среднее количество столкновений á z ñ за единицу времени, и какова средняя длина пробега молекулы á l ñ от одного столкновения до другого? Минимальное расстояние, на которое могут сблизиться молекулы, называется эффективным диаметром молекулы (d). Он зависит от скорости сталкивающихся молекул, а значит от температуры газа.
.
Для определения á z ñ представим себе такую упрощенную модель: молекула в виде шарика диаметром d, которая движется среди других «застывших» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d (рис. 2.1). Можно представить, что это будет совершаться в некоторой области, которая по форме будет близка к цилиндру. В объёме V данного цилиндра среднее количество столкновений молекулы за секунду равно
á z ñ = n V á v ñ = np d 2á v ñ.
Если учесть движения остальных молекул, то
á z ñ =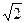 
np d2 á v ñ,
тогда средняя длина свободного пробега обратно пропорциональна концентрации молекул
.
При нормальных условиях á l ñ = 7×10-8 м. Длину свободного пробега молекул можно определить экспериментально на основе изучения явлений переноса в газах.
Законы физической кинетики
Диффузия. При диффузии наблюдается перенос как однородных, так и разнородных газов. В результате этого происходит постепенное перемешивание масс газа, перенос массы газа. В химически чистых газах при постоянной температуре диффузия возникает вследствие неодинаковой плотности в различных частях объема газа. Явление диффузии для химически чистого газа подчиняется закону Фика:
.
Плотность потока массы вещества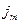 
, проходящего через единичную площадку, пропорциональна коэффициенту диффузии 
(измеряется в м2/с),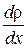 
- градиент плотности, равный скорости изменения плотности на единице длины х. Знак минус показывает, что перенос масс происходит в направлении убывания плотности. Коэффициент диффузии численно равен плотности потока массы при градиенте плотности, равном единице. Согласно кинетической теории газов:
|
|
|
.
Поскольку средняя длина свободного пробега молекул обратно пропорциональна концентрации молекул n [см. уравнение (2.4)], а давление р тем больше, чем выше n, то коэффициент диффузии обратно пропорционален давлению газа.
Вязкость. Механизм внутреннего трения между параллельными слоями газа или жидкости, которые движутся относительно друг друга с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями. В результате этого импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.
Сила внутреннего трения между слоями газа (жидкости) подчиняется
Закону Ньютона
,
h - динамическая вязкость, или коэффициент внутреннего трения, или коэффициент вязкости; dv / dx – градиент скорости, показывающий быстроту изменения скорости в направлении х, которое перпендикулярно направлению движения слоев; S – площадь, на которую действует сила F.
Взаимодействие двух слоев согласно второму закону Ньютона можно рассматривать как процесс, при котором изменение импульса одного слоя по отношению к другому за единицу времени равно по модулю действующей на каждый слой силе. Тогда плотность потока импульса
.
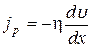Знак минус указывает на то, что импульс переносится в направлении убывания скорости.
Динамическая вязкость h численно равна плотности потока импульса при градиенте скорости, равном единице, и вычисляется по формуле:
.
Поскольку плотность r прямо пропорциональна давлению р, а длина свободного пробега á l ñ обратно пропорциональна давлению, то коэффициент внутреннего трения не зависит от давления. Он определяется главным образом природой химических веществ и температурой.
Закон Ньютона для внутреннего трения используется, например, при выводе так называемой формулы Пуазейля, определяющей объём V вязкой жидкости, которая протекает за время t по трубе радиуса r и длины l из-за разницы давлений на краях трубы, равной Δ p:
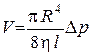. (2.1)
Теплопроводность. В газах перенос тепла происходит от нагретой части с температурой Т 1к более холодной с температурой Т 2. Передача теплаосуществляетсявследствие постоянных столкновений молекул, имеющих большую кинетическую энергию с молекулами, энергия которых меньше. Постепенно идет процесс выравнивания средних кинетических энергий молекул. Перенос энергии в форме теплоты подчиняется закону Фурье
|
|
|
,
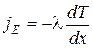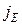-плотность теплового потока; l - коэффициент теплопроводности; 
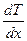- градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры.
Коэффициент теплопроводности
,
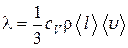где сV – удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме). Коэффициент теплопроводности l измеряется в Вт/(м×К).
Итак, в газах явления диффузии, вязкости и теплопроводности имеют немало общего:
1) все эти явления обусловливаются переносом: явление диффузии – переносом массы, явление теплопроводности – переносом энергии, явление вязкости – переносом импульса;
2) все явления сопровождаются рассеянием энергии;
3) в механизме всех трех явлений большую роль играет средняя длина свободного пробега á l ñ.
Сравним формулы, которые описывают явления переноса (табл. 2.1). Из формул вытекают простые зависимости между l, D иh:
h = r D;
; 
.
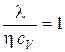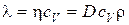Таблица 2.1
|
|
|
