Свойства функций входных сопротивлений и проводимостей пассивных 2хполюсников. Приемы построения 2хполюсных схем по заданным функциям Z(p) , Y(p).

Св-ва пассивной 2хполюсной цепи полностью определяются зав-тью ее вх. сопр-я или вх. проводимости от частоты ω (или параметра p). При синтезе цепи важно: какими могут (не могут) быть ф-ции Z(p) или Y(p). Если по этим ф-циям можно построить соответствующую эл. цепь, то их наз-ют физически реализуемыми. Входное сопр-е 2хполюсника в операторной форме:

Реализуемая ф-ция сопротивления (проводимости) должна иметь вид рациональной дроби. Сопр-е реальной цепи токам высоких частот может иметь активный характер при n=m, индуктивный характер и вид Lp, при n–m=1 и или емкостный характер и вид 1/ (Сp), при n–m=–1и . Коэффициенты и д. быть вещ. и положи.. Многочлены в числителе и знаменателе рациональной дроби можно представить в виде произведения множителей вида (p–p_i), где p_i – корни многочленов P(p) и Q(p):

Значения переменного p, соответствующего корням многочлена Р(р), наз-ют нулями функции Z(p), а соотв. корням Q(p) – полюсами функции Z(p). Нули и полюсы ф-ции вх. сопр-я должны иметь отриц. вещественную часть. Собственные колебания цепи должны быть затухающими. Это условия физической реализуемости Z(p) в виде пассивной цепи.

Если удовлетвор-ая усл-ям физ. реализуемости и достаточно сложная Z(p) задана выр-ем, то по ней нельзя сразу составить схему 2хполюсника с соответствующим сопротивлением.

1. Ф-цию Z(p) надо представить в виде более суммы более простых слагаемых (схема 2хполюсника получается последовательным соединением простых ветвей);

2. заданную рациональную дробь можно представить в виде цепной дроби (схема – в виде цепочки, содержащей чередующиеся последовательные и параллельные ветви);

3. Функцию Y(p) можно разложить на простые слагаемые (схема 2хполюсника получается парал-ным соединением простых ветвей);

4. Функцию Y(p) можно разложить в цепную дробь.

Т.о. по заданной ф-ции Z(p) можно построить 4 схемы 2хполюсников с одинаковой зав-тью сопр-я от частоты. Такие 2хполюсники наз-ся эквивалентными.

Пусть ф-ция сопр-я некоторого

2хполюсника

Можно построить 2хполюсник с

сопр-ем .

Произведение сопр-й этих 2хполюсников не зав. от частоты . Такие два 2хполюсника с сопр-ями Z₁(p) и Z₂(p) наз-ют взаимообратными. Они имеют взаимообратные св-ва: если Z₁(p)→0, то Z₂(p)→∞, и наоборот.

5. Трехэлементные реактивные 2хполюсники (схемы, частотные зав-ти Z(ω), определение резонансных частот, понятия и примеры взаимно обратных и эквивалентных 2хполюсников). Общие свойства реактивных 2хполюсников.

Из 3х реактивных эл-тов можно составить 4 схемы 2хполюсников:

 

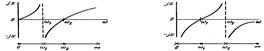1 и 2 пропускают постоянный ток, принятый за ток с нулевой частотой, и оказывают токам с высокими частотами высокое сопр-е. 3 и 4 постоянный ток не пропускают и имеют малое сопр-е на высоких частотах. Рассм. порядок построения графика зав-ти сопр-я от частоты на примере 2хполюсника 1. При нулевой частоте сопр-е 2хполюсника равно 0. На резонансной угловой частоте парал-ного соед-я сопр-е 2хполюсника →∞ и скачком меняет знак. Индуктивная проводимость становится меньше емкостной – резонанс токов. На некоторой частоте ω₂ наступает равенство сопр-я контура L₁C₁ индуктивному сопр-ю ω₂L₂ – резонанс напряжений.

2хполюсники 1 и 2 обратны 2хполюсникам 3 и 4.

Для 2хполюсника 1:

Для 2хполюсника 2:

Для 2хполюсника 3:

Для 2хполюсника 4:

При соответствующем подборе элементов 2хполюсники 1 и 2 эквивалентны друг другу и обратны 2хполюсникам 3 и 4.

Общие св-ва реактивных 2хполюсников:

1. число резонансов реакт. 2хпол. на конечных частотах на 1 меньше числа элементов в нем; 2. для реакт. 2хпол. существует взаимно-обратный и эквивалентный 2хпол.;

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: