 |
Цепочечное соединение 4хполюсников. Определение параметров соединения.
|
|
|
|
 |
При цепочечном соединении 2х 4хполюсников:
; 
; 
;
; 
; 
.
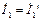Тогда для определения параметров соединения воспользуемся уравнениями передачи:
; 
; 
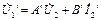Отсюда получим:
Группируя члены этих уравнений и убирая штрихи, получим:
Полученные ур-я ввязывают напряжение и ток на входе с напряжением и током на выходе.
Если 4хполюсники, входящие в цепочечное соединение характеризовать матрицей 
, то все соединение можно охарактеризовать матрицей:
Матрица (А) цепочечного соединения 4хполюсников – произведение матриц 
и 
4хполюсников, входящих в это соединение.
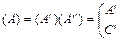
Корректоры группового времени прохождения сигналов (фазовые корректоры). Порядок синтеза схемы корректора с заданными с-вами.
Если фазовая скорость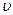 
для различных частотных составляющих неодинакова, то сигнал при передаче подвергается фазочастотным искажениям.
Значение tгр пр на определенной частоте 
хар-ет время запаздывания огибающей группы частотных составляющих сигнала, лежащих в узкой полосе частот вблизи ω1. Для цепи с сосредоточенными параметрами
Для устранения ФЧ искажений используют корректоры группового времени прохождения. Фазовые хар-ки используемых в качестве корректоров 4хполюсников подбирают так, чтобы время прохождения в откорректированном тракте с включенным корректором 
не зависело от частоты, т.е.
- фазовая хар-ка откорректированного тракта.
Мостовая схема с взаимообратными сопротивлениями:
; 
; 
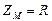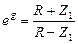
Независимость ZМ от частоты позволяет хорошо согласовать эти схемы с нагрузками. При реактивных сопр-ях Z1 и Z2:
; 
Значит 
; 
; 
; 
Отсюда 
Фазовый контур 1ого порядка:
 |
; 
; 
; 
. Отсюда 
, где k=L/R
Функция передачи: 
|
|
|
Фазовый контур 2ого порядка:
 |
; 
; 
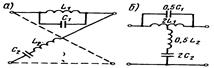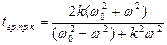
Цепи с распределенными параметрами. Первичные параметры электрической линии. Решение диф. ур-й линии для установившегося режима переменного тока.
При большой длине соединительных проводов, т.е. передаче эл. энергии по линии, длина кот. соизмерима с длиной волны эл/магн. Колебания, нельзя не учитывать сопр-е, индуктивность и емкость, распределенные по всей ее длине. Эл. и магн. Поля в этом случае распределены вдоль линии и пространственно совмещены. Такая линия – эл. цепь с распределенными параметрами.
Для получения исходных соотношений, определяющих процессы в цепях с сосредоточенными параметрами, используют первичные параметры: сопр-е проводов R (Ом/км), их индуктивность L (Гн/км), проводимость изоляции G (1/Ом·км), емкость проводов С (Ф/км).
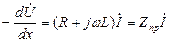
Это диф. ур-я линии.
Продиф-ем 1ое Ур-е по х:
=> 
Обозначим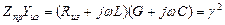 
, тогда:
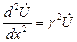, γ – коэффициент распространения волны
Отсюда 
Соответственно для тока:
=> 
Причем 
, где ZB – волновое сопр-е линии.
Решение системы диф. ур-й:
Где 
Величины γ и ZB – вторичные параметры линии.
Анализ решения диф. ур-й линии. Волновые процессы в линии (падающие и отраженные волны напряжения и тока в линии, волновые параметры линии).
Пусть x=0, тогда 
, где А1 и А2 – составляющие напряжения. Будем писать вместо А1 и А2 
и 
.
Рассм. 1ое слагаемое ур-я 
.
Полагая, что 
получим 
На комплексной плоскости это выр-е изображают вращающим вектором с нач. фазой – βх. Это выр-е математически представляет собой волну, движущуюся от начала линии к ее концу – падающую.
Рассм. 2ое слагаемое:
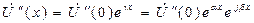
- мгнов. Значения
Это ур-е соответствует волне, движущейся от конца линии к ее началу – отраженной.
Напряжение в каждой точке линии равно сумме падающей и отраженной волн:
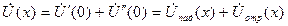
А ток:
Волновое сопр-е определяет отношение напряжения к току в отдельной волне (падающей или отраженной) в любой точке однородной линии.
|
|
|
Величины γ и ZB – вторичные (волновые) параметры линии.
|
|
|
