 |
Влияние графического моделирования на формирование умения решать задачи разными способами
|
|
|
|
Среди различных видов работы над уже решенной задачей (работа над задачей после ее решения) особое место занимает решение задачи другим способом. Хотя в начальной школе выбор различных способов решения задачи в большинстве случаев связан с использованием свойств арифметических действий (сложения, вычитания, умножения, деления), следует стремиться к тому, чтобы учащиеся сознательно выбирали наиболее рациональный из известных им способов.
Решение задач различными способами способствует развитию логического мышления и математических способностей учащихся.
Ранее уже говорилось, что эффективным способом отыскания различных способов решения задачи является ее графическое моделирование. Происходит это потому, что строя графические модели задачи, мы освобождаем учащихся от восприятия несущественных особенностей условий, представляем существенные особенности в наглядной форме и тем самым помогаем детям установить все возможные связи и зависимости между величинами, что, в свою очередь, облегчает детям нахождение различных способов решения.
Приведем несколько примеров работы над такими задачами и покажем, как при этом графические иллюстрации облегчают нахождение путей их решения различными способами. Иными словами, графическая модель задачи сама по себе является средством подведения ребенка к пониманию того, что задача может быть решена разными способами.
Мама купила 2 батона, по 8 рублей каждый. В кассу она подала 20 рублей/Сколько сдачи должна получить мама?
Схема к данной задаче подводит учащихся к одному способу решения:
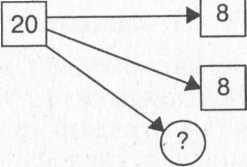
По этой схеме дети составляют выражение: (20 - 8) - 8. Второй способ решения на этой схеме не просматривается. Если же использовать графическую модель в отрезках, то на ней явно видны оба способа решения:
|
|
|

1.20-(8+ 8)
2. 20 - 8 - 8
На примере таких задач удобно показывать детям необходимость постепенного перехода к более высоким ступеням графической абстракции при решении задач: чем абстрактнее модель, тем больше «степеней свободы» она имеет.
Девочка нашла 36 грибов, а мальчик 28. Среди этих грибов оказалось 3 несъедобных. Сколько съедобных грибов нашли дети?
Графическая модель данной задачи дает возможность по одному рисунку составить все три возможные решения задачи:

1) (36 + 28) - 3
2) (36 - 3) + 28
3) (28-3)+ 36
Схематические изображения для каждого способа решения надо делать разные. В данной задаче их полезно сделать по готовым решениям и объяснить ход мысли при составлении каждой схемы.
Например:
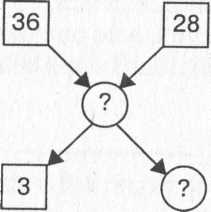
Рассуждение:
Сначала дети высыпали все грибы вместе на полянку, а затем отобрали три несъедобных и выбросили. Значит сначала найдем, сколько грибов было всего, а затем отнимем несъедобные — их было 3.
В магазин привезли 12 ящиков с яблоками по 8 кг в каждом. До обеденного перерыва было продано 9 ящиков. Сколько килограммов яблок осталось продать после обеденного перерыва?
Анализируя текст, строим графическую модель.
— Обозначим отрезком все ящики с яблоками, которые привезли в магазин.
— Сколько килограммов яблок было в каждом ящике? (8 кг.) Обозначим это на чертеже.
— Сколько ящиков продано? (9.) Обозначим на чертеже эти 9 ящиков. Покажите на чертеже те ящики, что остались.
— Что надо узнать в задаче? (Сколько кг яблок осталось.) Обозначим на рисунке искомое знаком вопроса.

По чертежу легко увидеть различные способы решения:
1 способ: 8-12-8-9 = 24 (кг)
2 способ: 8 • (12 - 9) = 24 (кг)
Роль графической модели при нахождении разных способов решения задач «на движение» была показана выше.
В заключение приведем несколько нестандартных задач, на примере которых можно со всей убедительностью показать высокую практическую эффективность графической модели как опоры для осознанных мыслительных действий при решении задачи.
|
|
|
Девочка сыграла на чемпионате школы 22 партии в шахматы. 2 партии она проиграла, а из остальных на каждые 2 партии вничью, у нее 3 выигранных. Сколько побед у девочки?
Обозначим на модели нулем — ничью, плюсом — выигрыш. Если начертить отрезок длиной 22 клетки, то задачу можно решить графическим способом, подсчитав по рисунку количество выигрышей.
Опора на графическую модель приводит к следующим выводам:
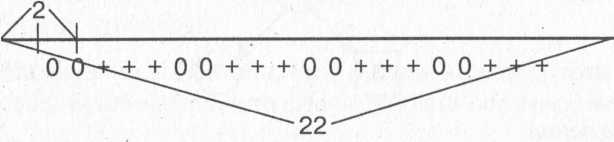
а) выигрышей 3 • 4 = 12;
б) проигрышей 2• 4 = 8.
Внук спросил дедушку: «Сколько тебе лет?» Дедушка ответил: Если проживу еще половину того, что я прожил, да еще один год, то мне будет сто лет. Сколько лет дедушке?
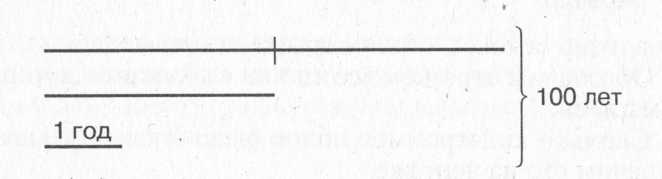
Анализируя графическую модель, получаем решение:
1) 100 - 1 = 99 (лет)
2) 99: 3 = 33 (года)
3) 33- 2 = 66 (лет)
Мама купила 4 кг яблок. Расплачиваясь за них, она получила 40 рублей сдачи. Если бы мама купила 6 кг яблок, то ей пришлось бы доплатить 40 рублей. Сколько стоил 1 кг яблок?
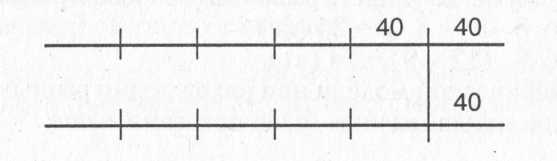
Анализ графической модели приводит к выводу, что цена 1 кг яблок 40 рублей.
Сумма трех чисел равна 18. Первое число в 2 раза больше второго, а второе в 3 раза меньше третьего. Найдите эти числа.
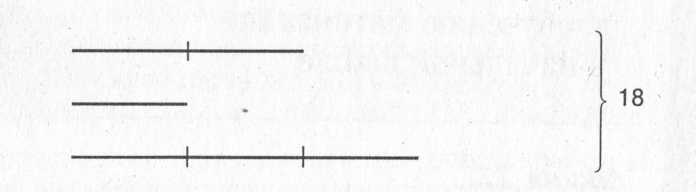
Анализируя графическую модель, получаем: I число — 6; II число — 3; III число —9.
Обучение младших школьников решению задач — процесс длительный, методически неоднозначный и сложный даже для учителей с большим стажем работы. Опыт работы автора данного пособия в системе повышения квалификации учителей подтверждает это. С целью более детального анализа всех видов встречающихся в курсе математики начальных классов задач и подробного анализа методики работы с ними, автором данного пособия была написана книга для учителя «Обучение решению задач в начальных классах» (М., 2003). При подготовке к практическим занятиям, а также при подготовке к выходу на учебную практику в школу студентам рекомендуется обратиться к этой книге. В ней рассмотрены методика работы над всеми типовыми и производными от типовых задач, встречающимися в различных учебниках для начальных классов, а также вопросы обучения решению задач повышенной сложности при проведении факультатива или кружка по математике.
|
|
|
Глава 9
|
|
|


