 |
Спектральная объемная плотность потока энергии собственного
|
|
|
|
Спектральная объемная плотность потока энергии собственного
излучения газа
Как уже было отмечено ранее, газ излучает всем объемом. По аналогии с поверхностной плотностью под спектральной объемной плоскостью потока энергии излучения понимается количество теплоты, которое излучается в единицу времени элементарным объемом газа dV в элементарном интервале длин волн
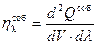 , Вт/м4. , Вт/м4.
| (13. 1) |
Величина интегрального потока собственного излучения газа Qсобзависит от его температуры, давления, химической природы, формы и размеров объема.
13. 2. Спектральная угловая объемная плотность (спектральная яркость) потока энергии собственного излучения газа
Эта характеристика служит для описания распределения энергии объемного излучения по различным направлениям в пространстве и определяется выражением, Вт/(м4∙ ср)
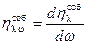 , ,
| (13. 2) |
где dω – элементарный телесный угол, ср.
Если спектральная яркость объемного излучения не зависит от направления в пространстве, то такое излучение называется изотропным и тогда
 . .
| (13. 3) |
При неизотропном излучении полная спектральная объемная плотность потока энергии (полная спектральная яркость) собственного излучения газа равна
 . .
| (13. 4) |
Величину полной спектральной яркости собственного излучения газа можно определить следующим образом. Пусть в качестве внешнего по отношению к газу источника излучения выступает некоторая элементарная площадка dF. Обозначим величину изменения спектральной яркости излучения внешнего источника на элементарном пути dr внутри газа через dBλ , а первоначальную яркость через Bλ .
Согласно закону Бугера отношение величины изменения яркости к величине первоначальной яркости излучения пропорционально толщине dr элементарного слоя, т. е.
|
|
|
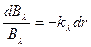
|
или
 .
где .
где  -спектральный коэффициент поглощения среды, 1/м. -спектральный коэффициент поглощения среды, 1/м.
| (13. 5) |
Знак “–“ указывает на то, что яркость уменьшается вследствие поглощения энергии излучения газом. Формула (3. 17) справедлива для случая только поглощающего газа.
Уравнение переноса энергии в излучающе-поглощающей среде.
Рассмотрим этот же процесс переноса энергии в поглощающем и излучающем газе. Тогда на пути dr имеют место два процесса: первый – поглощение энергии внешнего источника газом, второй – излучение газом собственной энергии. Учитывая вклад энергии собственного излучения газа, уравнение (3. 20) можно записать в виде:
 . .
| (13. 6) |
Последнее выражение представляет собой уравнение переноса энергии излучения в поглощающей и излучающей газовой среде.
Предположим, что однородный поглощающий и излучающий газ заключен в твердую излучающую оболочку, температура, которой равна температуре газа, и между газом и оболочкой имеет место термодинамическое равновесие.
Поскольку спектральная яркость равновесного (абсолютно черного) излучения оболочки не зависит от направления и равна: 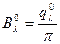 , то для условия термодинамического равновесия (энергия, поглощенная газом, компенсируется энергией собственного излучения газа) можно записать:
, то для условия термодинамического равновесия (энергия, поглощенная газом, компенсируется энергией собственного излучения газа) можно записать: 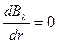 , и тогда
, и тогда
 . .
| (13. 7) |
Следовательно, спектральная яркость объемного излучения газа равна
 , ,
| (13. 8) |
а спектральная объемная плотность 
 . .
| (13. 9) |
Из (13. 9) следует ранее сказанное утверждение: в окнах прозрачности, т. е. когда kλ = 0, газ не поглощает проходящую через него энергию и, в соответствии с законом Кирхгофа, не излучает энергию (при kλ = 0, η λ соб = 0).
Уравнение 3. 18 записано с использованием спектральных величин. Однако при использовании серого приближения это уравнение можно записать в таком виде для интегрального излучения (без индекса монохроматического излучения).
|
|
|
Как уже было отмечено ранее, излучение, распространяющееся в излучающей и поглощающей среде, ослабляется за счет поглощения и одновременно усиливается за счет собственного излучения среды. Этот процесс и описывается уравнением переноса энергии. Уравнение переноса энергии является аналогом закона Бугера, записанного для случая, когда учитывается вклад собственного излучения среды. По своей форме уравнение 3. 18 является дифференциальным уравнением первого порядка. Оно позволяет детально исследовать поле интенсивности излучения и получить уравнения теплообмена излучением. Как и для любого дифференциального уравнения для его решения требуется записать граничные условия, характеризующие количественные характеристики излучения на границе излучающей системы (плотность потока энергии излучения, исходящего из любой точки поверхности; степень черноты в данной точке поверхности в направлении излучения; интенсивность излучения абсолютно черного тела при температуре поверхности в данной точке; направленная отражательная способность граничной поверхности в данной точке для направления падающего излучения, интенсивность падающего в данную точку поверхности излучения и др. ). Интегрирование уравнения переноса энергии вдоль выбранного направления, исходящего из любой точки поверхности, до выбранной точки объема среды позволяет определить характеристику интенсивности излучения в выбранном направлении в выбранной точке объема среды, заполняющей анализируемую систему. При этом должны быть известны поля температур и радиационные характеристики в объеме среды на граничной поверхности для расчета энергии собственно излучения этих сред.
Интегрирование дифференциального уравнения переноса излучения совместно с граничными условиями позволяет получить интегральные уравнения радиационного теплообмена для поверхностей и объемных плотностей потоков энергии различных видов излучения.
Аналитическое решение подобных уравнений весьма сложно из-за необходимости интегрирования по поверхности и объему.
|
|
|
Из приближенных методов решения интегральных уравнений теплообмена в системах с излучающей и поглощающей средой широко используются различные зональные методы.
|
|
|


