 |
Спектральная степень черноты газа и газового объема
|
|
|
|
Спектральная степень черноты газа и газового объема
Спектральной степенью черноты газа для данного направления ε λ (r) называется отношение спектральной яркости собственного излучения газа в направлении r к спектральной яркости излучения а. ч. т., имеющего температуру газа. Применяя к излучению газа закон Кирхгофа, запишем
 .
|
Следовательно, с учетом (3. 7)
 .
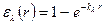| (13. 10) |
Интегрируя величину ε λ (r) по всем направлениям полусферы, т. е. в пределах телесного угла 2π и заменяя бесконечное множество длин пути луча r эффективной длиной пути луча lэф для конкретной формы и размеров объема поглощающего и излучающего газа, можно получить выражение для расчета полной спектральной степени черноты газового объема
| (13. 11) |
Сравнение (13. 11) и (12. 9) показывает, что в соответствии с законом Кирхгофа спектральная поглощательная способность газового объема численно равна его спектральной степени черноты.
Зная величину ε λ , можно рассчитать спектральный поток энергии собственного излучения газа. Предположим, что объем V излучающего газа ограничен условной поверхностью F с температурой, равной температуре газа (случай термодинамического равновесия). Тогда излучение объема можно представить как излучение поверхности, степень черноты которой равна ε λ
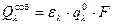
| (13. 12) |
Интегральные радиационные характеристики газового объема
В большинстве случаев при практических расчетах теплообмена излучением используются интегральные радиационные характеристики газового объема - интегральная поглощательная способность и интегральная степень черноты.
Предположим, что на газовый объем от внешнего источника падает поток энергии излучения Qпад, Вт. Часть энергии поглощается газом Qпогл, остальная часть пропускается объемом газа. Отношение потока энергии поглощенного газом, к падающему потоку называется интегральной поглощательной способностью газового объема
|
|
|
 .
|
Если известен спектр полос поглощения газа и спектральный состав падающего излучения, то связь между спектральной поглощательной способностью газового объема и его интегральной поглощательной способностью определяется выражением
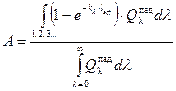
| (14. 1) |
В формуле (14. 1) знак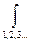 
означает интегрирование по полосам 1, 2, 3… спектра длин волн. Как следует из этой формулы, интегральная поглощательная способность газового объема зависит от эффективной длины пути луча, т. е. от формы и размеров газового объема, от спектральных свойств газа и от спектрального состава падающего на газ излучения, от температуры и давления газа. Для серого газа kλ не зависит от длины волны и есть величина постоянная, т. е. kλ =k. Тогда 
.
Интегрируя формулу (13. 12) в пределах полос излучения газа, получим величину интегрального потока энергии собственного излучения газового объема с температурой Т
 ,
|
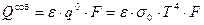откуда
.
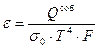Величина ε называется интегральной степенью черноты газового объема.
По аналогии с формулой (14. 1) можно записать
 .
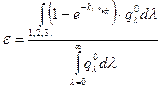| (14. 2) |
Из формулы (14. 2) следует, что интегральная степень черноты газового объема зависит от свойств газа, формы и размеров объема, температуры и давления газа.
Модель серого приближения
Для расчетов интегральной степени черноты газового объема часто используется модель серого приближения. Газ считается серым, если спектральный коэффициент kλ не зависит от длины волны и во всем спектре полос излучения газа есть величина постоянная и равная k. Для серого газа интегральная поглощательная способность не зависит от спектрального состава падающего на газ излучения и равна спектральной поглощательной способности Aλ =A. В соответствии с законом Кирхгофа для серого газа A=ε и Aλ =ε λ , где 
.
|
|
|
Для смеси двух газов закон аддитивности не выполняется вследствие наложения полос излучения, поэтому для смеси интегральная степень черноты равна
 ,
| (14. 3) |
где ε 1 и ε 2- степени черноты, рассчитанные в предположении, что смесь состоит только из одного газа 1 или 2 (так называемые “парциальные степени черноты”).
В зависимости от требуемой точности решения задачи используются различные расчетные методики для определения радиационных характеристик газового объема: полный селективный расчет с учетом каждой линии спектра и особенностей ее деформации при изменении температуры и парциального давления газа; использование модели каждой полосы; модель ступенчатого приближения полос (квазисерое приближение). Чаще всего в расчетах используется модель серого приближения с использованием интегральных величин степени черноты и поглощательной способности газового объема.
На практике интегральная степень черноты H2O, CO2 определяется с помощью номограмм, построенных по экспериментальным данным, рис. 14. 1 и 14. 2, учитывающих температуру и парциальное давление газа в смеси. Парциальное давление 
или 
в смеси определяется как произведение его содержания в долях на абсолютное давление смеси. Если давление смеси равно атмосферному, то долю газа надо умножить на 105 Па.
Величина степени черноты водяного пара 
, определенная по номограмме рис. 14. 1, должна быть умножена на поправку β , учитывающую парциальное давление H2O (водяной пар строго не подчиняется закону Бугера). Величина поправки определяется по графикам, представленным на рис. 14. 3.
Суммарная степень черноты смеси CO2 и H2O рассчитывается по формуле:
 .
| (14. 4) |
Величина поправки ∆ ε определяется по графикам рис. 14. 4. Для упрощенных расчетов можно принять ∆ ε =0.
Как было отмечено ранее, собственное излучение газов не подчиняется закону Стефана–Больцмана. Однако для упрощения расчетов считается, что излучение газов подчиняется указанному закону, а все особенности излучения газов учитываются при расчете степени черноты.
|
|
|
Рассмотренные выше соотношения справедливы для чистых поглощающих и излучающих газов и их смесей. Описание излучения и расчет теплообмена излучением существенно усложняется при наличии в газах твердых частиц. Примером таких смесей являются дисперсные системы: запыленные газы, светящиеся пламена, аэрозоли и т. д. При наличии в газах твердых частиц общее ослабление потока энергии проходящего через газ излучения определяется не только поглощением газом, но и поглощением твердыми частицами и рассеянием (отражением) излучения твердыми частицами.
Под рассеянием понимается дифракционное отражение излучения, зависящее от соотношения размера частиц и длины волны падающего излучения. Радиационные свойства совокупности частиц определенного вещества отличаются от свойств твердого тела из этого вещества и определяются: размерами частиц, распределением частиц по размерам (для полидисперсных систем), длиной волны излучения, концентрацией частиц в объеме газа, расстоянием между частицами, электромагнитными свойствами вещества частиц.
Твердые частицы можно считать независимыми, если расстояние между ними в газовом объеме в два и более раза превышает длину волны падающего излучения. Соотношение между поглощением и рассеянием определяется безразмерным параметром 
, где d – диаметр частиц, λ – длина волны излучения. Рассеянием можно пренебречь, при ρ < < 1. Распределение рассеянного излучения по направлениям сферы зависит также от размера частицы: чем крупнее частица, тем больше рассеянное излучение сосредотачивается в направлении падающего луча. При значениях ρ < 1 распределение по направлениям рассеянного излучения приближается к изотропному. Теплообмен излучением в дисперсных системах рассматривается в специальной литературе.
|
|
|
