 |
15.1. Обобщенные угловые коэффициенты излучения и их свойства
|
|
|
|
При расчете теплообмена излучением в системах, заполненных поглощающим и излучающим газом, необходимо, как и в случае систем с лучепрозрачной средой, учитывать взаимное расположение твердых поверхностей, ограничивающих газовый объем. Отличие заключается в том, что на любую поверхность от всех других попадает не просто часть эффективного потока, а часть эффективного потока, прошедшая через поглощающий газ. Очевидно, что прошедший поток будет меньше, чем в случае лучепрозрачной среды, так как часть энергии поглощается газом. Поэтому при расчетах используются обобщенные угловые коэффициенты для каждой пары поверхностей, в том числе и при излучении самой поверхности на себя.
Обобщенный угловой коэффициент излучения ψ ik с зоны i на зону k показывает, какая доля эффективного потока энергии излучения Qiэф, ушедшего в пределах полусферического телесного угла 2π с поверхности i, попала на поверхность k, Qkпад, с учетом поглощения части потока газовой средой:
 .
| (15. 1) |
Если система состоит из n поверхностей, то полная величина падающего на поверхность k потока равна:
 .
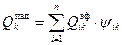| (15. 2) |
Из определения обобщенного углового коэффициента излучения следует, что его величина может изменяться в пределах от нуля до единицы и не имеет размерности.
Заметим, что, как и в случае лучепрозрачной среды, рассматривается только случай прямого обмена энергией между парой поверхностей.
Различают элементарные, локальные и средние обобщенные угловые коэффициенты излучения. Смысловое содержание этих коэффициентов аналогично случаю систем с лучепрозрачной средой. В дальнейшем будем использовать только средние, или просто обобщенные угловые коэффициенты излучения, которые обладают некоторыми свойствами. Свойства взаимности, невогнутости, аддитивности, затеняемости формулируются так же, как и для средних угловых коэффициентов излучения. Для замкнутых систем так же выполняется закон сохранения энергии, однако записывается он в форме, отличной для случая системы с диатермичной средой.
|
|
|
Если обозначить число поверхностных зон n, объемных зон m, а общее число поверхностных и объемных зон l=n+m, то с учетом поглощения излучения объемными зонами свойство замыкаемости запишется в виде:
 .
| (15. 3) |
Без учета поглощения объемными зонами формула (15. 3) принимает вид:
 ,
|
что соответствует свойству замыкаемости средних угловых коэффициентов излучения для систем с лучепрозрачной средой.
Для вывода формул, определяющих обобщенное условие коэффициента излучения, по аналогии со случаем систем с лучепрозрачной средой, рассмотрим три случая.
Элементарный обобщенный угловой коэффициент излучения
Величина элементарного потока энергии излучения, 
, падающего на элементарную площадку dF2 от всего эффективного потока, уходящего с площадки dF1 в пределах полусферы, по определению равна (рис. 5. 1)
где пропускательная способность слоя среды
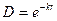
Принимая допущение, что среда и поверхности обладают свойствами серого тела, можно написать
По аналогии
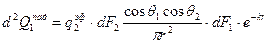
В последних выражениях величины
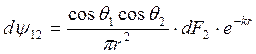
называются элементарными обобщенными угловыми коэффициентами излучения соответственно с dF1 на dF2 и с dF2 на dF1. В случае лучепрозрачной среды интегральный коэффициент поглощения k=0 и элементарные обобщенные коэффициенты излучения превращаются в элементарные коэффициенты 
и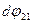 
.
Линейный обобщенный угловой коэффициент излучения
Рассматривая теплообмен излучением в системе dF1-F2 и dF2-F1можно написать
|
|
|
и 
В последних выражениях величины
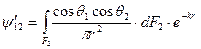
и 
называется локальными обобщенными угловыми коэффициентами соответственно с dF1 на F2 и с dF2 на F1.
Средний обобщенный угловой коэффициент излучения
При анализе теплообмена излучением между двумя поверхностями площадью F1 и F2, очевидно
и 
Полагая, что в пределах поверхности F1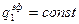 
, а в пределах F2 
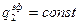, и зная, что
, 
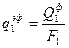получим
и 
В последних выражениях величины
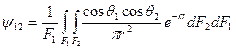
и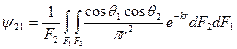 
называются средними обобщенными угловыми коэффициентами излучения соответственно с с F1 на F2 и с F2 на F1.
В случае, когда поглощение среды отсутствует (k=0) последние коэффициенты превращаются в средние угловые коэффициенты излучения 
и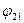 
.
Расчет величин средних обобщенных угловых коэффициентов излучения по вышеприведенным формулам представляет собой сложную задачу, так как, во-первых, требуется интегрирование по поверхности и, во-вторых, необходимо знать радиационные свойства самой среды.
|
|
|
