 |
Классический зональный метод расчета теплообмена излучением в системах с поглощающей и излучающей средой
|
|
|
|
Сущность зонального метода расчета теплообмена излучением, как и в случае систем с лучепрозрачной средой, заключается в делении системы на n поверхностных и m объемных зон и замене непрерывного распределения температуры и радиационных свойств кусочно-непрерывным распределением этих характеристик. Каждая поверхностная и каждая объемная зона считается изотермической и изооптической. Поверхность системы F и объем газа V равны соответственно сумме поверхностей зон и сумме объемов зон, т. е.
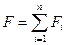 , ,  . .
|
В результате применения зонального метода интегральные уравнения теплообмена излучением заменяются замкнутой системой линейных алгебраических уравнений. Решением этой системы уравнений определяются неизвестные величины, которыми являются результирующие потоки при фундаментальной постановке задачи или температуры при обратной для каждой поверхностной и объемной зоны.
Для вывода основных уравнений зонального метода расчета теплообмена излучением рассмотрим систему, состоящую из n поверхностных зон и m объемных зон.
Присвоим индекс i=1, 2, …, n поверхностным, а индекс j=1, 2, …, m объемным зонам (рис. 15. 1).
Принимаем, что в пределах каждой объемной зоны коэффициент поглощения газа kj постоянен, тогда степень черноты объемных зон равна:
 , ,
| (15. 4) |
где ℓ эф, j- эффективная длина пути для каждой объемной зоны. С учетом этого поток энергии собственного излучения объемных зон рассчитывается по формуле:

| (15. 5) |
Для чистого незапыленного газа рассеяние излучения равно нулю, следовательно, отражательная способность газа так же равна нулю Rj=0 и эффективный поток объемных зон равен потоку энергии собственного излучения, т. е. Qjсоб=Qjэф, j=1, 2, …, m. С учетом последнего, для объемных зон можно использовать определение результирующего потока как разности поглощенного Qjпогл и собственного Qjсоб потоков
|
|
|
 . .
| (15. 6) |
Результирующий поток для любой зоны k по определению равен:
 , ,
| (15. 7) |
а поглощенный этой зоной поток:
 . .
| (15. 8) |
На зону k падает излучение как поверхностных, так и объемных зон. С учетом поглощения энергии объемными зонами и учитывая форму и размеры поверхностных и объемных зон, можно записать:
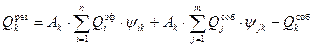 . .
| (15. 9) |
Первый член правой части уравнения (15. 9) представляет собой поглощенную зоной k часть потока, попавшего на нее со всех поверхностных зон, в том числе и с самой на себя, с учетом поглощения потоков при прохождении через газовый объем. Второй член правой части представляет собой поглощенную зоной k часть потока, попавшего на нее со всех объемных зон, с учетом поглощения потоков при прохождении объема газа.
При решении задачи расчета теплообмена излучением уравнение (15. 9) записывается для всех поверхностных и всех объемных зон. В результате получается замкнутая система линейных алгебраических уравнений, в которой число неизвестных равно сумме поверхностных и объемных зон. Для поверхностных зон используется уже известное соотношение:
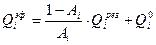
| (15. 10) |
Для серого приближения Аi=ε i.
Для проверки правильности решения задачи используется закон сохранения энергии: для замкнутой системы алгебраическая сумма результирующих потоков равна нулю.
Определение обобщенных угловых коэффициентов излучения представляет сложную задачу, и для этого используются специальные методики и справочная литература. Для простейших систем из двух или трех зон возможно решить задачу явным образом, путем исключения эффективных потоков из зональных уравнений. Рассмотрим несколько примеров.
|
|
|
Теплообмен излучением в системе из одной поверхностной и одной объемной зоны
Рассмотрим теплообмен излучением в системе из одной поверхностной и одной объемной зоны (система газ-оболочка). Считаем, что задана температура поверхности T1=const, степень черноты поверхности ε 1=const, температура газа T2=const, степень черноты газа ε 2=const, площадь поверхности F, обобщенные угловые коэффициенты излучения ψ 12, ψ 21, ψ 11, ψ 22.
При фундаментальной постановке данной задачи необходимо определить результирующие потоки для зон, т. е. Q1рез и Q2рез. В рассматриваемой системе из двух зон Q1рез + Q2рез = 0, следовательно
Q1рез= – Q2рез.
Поэтому достаточно определить один поток, например, Q1рез. Используя определение Qэф = Qотр + Qсоб, запишем зональные уравнения:
для первой поверхности
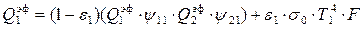 , ,
| (16. 1) |
для второй (объемной) зоны с учетом R2=0
 . .
| (16. 2) |
Уравнения (16. 1) и (15. 12) можно переписать, учитывая, что пропускательная способность газа D2 = 1 – A2 или для серого приближения D2 = 1 – ε 2.

| (16. 3) |
 . .
|
Обобщенные и средние угловые коэффициенты излучения ψ 21=1, φ 21=1, φ 22=0, φ 12=1, φ 11=0. Подставляя вместо Q2эф его значение, решая уравнение (16. 3) относительно Q1эф и учитывая выражение (15. 10) получим формулу Нуссельта:
 , ,
| (16. 4) |
где приведенный коэффициент излучения системы серый газ – серая оболочка равен:
 . .
| (16. 5) |
Коэффициенты излучения газа и оболочки определяются обычным образом: C1=ε 1∙ C0, C2=ε 2∙ C0.
|
|
|


