 |
Гидродинамическое подобие. Лекция №8. Гидромеханические процессы
|
|
|
|
Гидродинамическое подобие
Вспомним уравнения переноса количества движения или уравнения Навье-Стокса:
Пусть запишут сами в тетради себе.
Возьмем уравнение переноса импульса для какой-либо одной оси, например, оси Х:
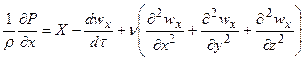
В случае одномерного движения это уравнение будет выглядеть так:
1 2 3 4
Чтобы представить дифференциальное уравнение в виде зависимостей между критериями подобия, необходимо:
1) отбросить знаки дифференцирования;
2) заменить x, y, z на неориентированные в пространстве геометрические размеры d или l;
3) разделить все уравнение на один из его членов.
Итак, в нашем случае мы будем делить на третий член уравнения:
1. 
– Критерий Эйлера, 
– характеризует влияние сил давления и инерции на движение жидкости.
2. 
– Критерий Фруда, 
; Х = g
характеризует влияние сил тяжести на движение жидкости.
3. 
– Критерий Рейнольдса,
характеризует влияние вязкости и сил трения на режим движения жидкости.
Таким образом, решение дифференциального уравнения может быть представлено критериальным уравнением вида: f(Eu, Fr, Re)=0 – Обобщенное критериальное уравнение.
Определяющим является критерий Эйлера:
Eu = f (Re, Fr)
Существует еще несколько критериев, описывающих движение жидкости:
Критерий гомохронности: 
– характеризует неустановившееся состояние процесса.
Критерий Галилея: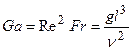 
Критерий Архимеда: 
– характеризует отношение разности сил тяжести и подъемной (действующих на частицы) к подъемной силе
Критерии Галилея и Архимеда применяются в случае свободного движения жидкостей, т. е. при естественной конвекции.
Лекция №8
1. Классификация гидромеханических процессов.
|
|
|
2. Осаждение в гравитационном поле.
3. Разделение газовых неоднородных систем: осаждение в центробежном поле.
4. Перемешивание.
Гидромеханические процессы
Гидромеханические процессы – это технологические процессы, протекание которых основано на закономерностях переноса импульса (mv).
Классификация гидромеханических процессов:
1) В зависимости от целенаправленности процесса:
а) Разделение неоднородных систем (осаждение, фильтрование и мокрая очистка);
б) Получение неоднородных систем (перемешивание и псевдоожижение);
в) Перемещение потоков: однофазное течение (гомогенная система) и двухфазные потоки (гетерогенная система).
Неоднородными называются системы, состоящие как минимум из двух фаз, т. е. они имеют поверхность раздела фаз.
| Две фазы
| |
| Внешняя фаза (дисперсионная среда), окружающая частицы внутренней фазы. | Внутренняя (дисперсная) фаза, частицы находящиеся в мелкораздробленном состоянии. |
Неоднородные системы
| Газовые | Жидкие |
| 1. Пыль (в газе твердые частицы, диаметром частиц от 7-100мкм); 2. Дым (в газе твердые частицы, диаметр 0, 3-3 мкм); 3. Туман (в газе капельки жидкости). | 4. Суспензии (в жидкости твердые частицы); 5. Эмульсии (в жидкости капельки другой жидкости); 6. Пены (в жидкости молекулы газа). |
| В общем случае подобные системы, состоящие из твердых или жидких частиц взвешенных в газообразной среде называются аэрозоли | Для эмульсии и пен характерно такое свойство как инверсия фаз – это переход дисперсной фазы в сплошную среду или наоборот. |
Разделение неоднородных систем проводится с целью:
1) Очистки жидкости и газа от содержащихся в них вредных примесей;
2) Извлечения ценных компонентов из жидкости или газа.
К методам разделения неоднородных систем относятся:
1) Осаждение;
2) Фильтрование;
3) Мокрая очистка газов.
|
|
|
Выбор того или иного метода зависит от концентрации дисперсных частиц, их размера, требований к качеству разделения, а также от разницы плотностей дисперсной и сплошной фаз и вязкости последней.
Эффективность разделения неоднородных систем характеризуется степенью очистки:
где с1, с2 – содержание дисперсной фазы на входе и выходе из аппарата;
η – степень очистки.
Физический смысл η: показывает, какая доля в % дисперсной фазы задерживается в аппарате.
|
|
|
