 |
Основное уравнение гидростатики
|
|
|
|
Основное уравнение гидростатики
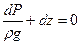или 
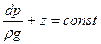
При условии, что плотность постоянна, то есть жидкость несжимаема.
Пример:
Рассмотрим сосуд, наполненный водой. Выделим две точки: одну на поверхности, другую на определенной глубине от плоскости отсчета.
 |
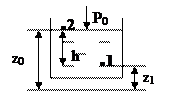Для этих двух точек запишем основное уравнение гидростатики:
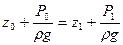
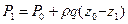
– Закон Паскаля.
Формулировка: Давление, создаваемое в любой точке покоящейся несжимаемой жидкости, передается одинаково всем точкам ее объема.
Сила давления на дно и стенки сосуда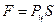 
Для плоских стенок (горизонтальные, вертикальные, наклонные) сила давления жидкости равна давлению в центре тяжести смоченной поверхности на площадь этой поверхности.
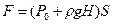
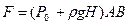– сила давления на дно сосуда
Гидродинамика
Гидродинамика – наука, изучающая законы движения жидкостей и практическое их применение.
Основные характеристики движения жидкостей
1) Расход жидкости – к оличество жидкости, протекающей через живое сечение потока в единицу времени. Бывает объемный, V, м3/с и массовый, G, кг/с.
Наличие вязкости, а также такого свойства как адгезия обусловливает различие скоростей частиц жидкости вдоль поперечного сечения потока и наличия различных режимов движения жидкости.
2) Режимы движения жидкости
| Ламинарный Слои движутся параллельно друг другу. Поперечные пульсации отсутствуют, перенос тепла происходит только в направлении движения, - значит продольный перенос. Механизм переноса тепла будет молекулярным. | Турбулентный
Неупорядоченное движение с интенсивным перемешиванием. Элементы потока – вихри движутся хаотически и составляют ядро потока.
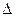 – толщина пограничного слоя, где происходит переход турбулентного режима в ламинарный.
Перенос тепла осуществляется двумя путями:
1) в ядре потока конвекцией и теплопроводностью 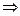 поперечный перенос;
2) в пограничном слое перенос осуществляется только теплопроводностью (т. к. нет поперечного движения потока).
|
В качестве примера рассмотрим перенос тепла через движущийся поток жидкости.
|
|
|
 | |||
 | |||
Переход от ламинарного течения к турбулентному, происходит тем легче, чем больше массовая скорость жидкости ρ w и диаметр трубы d и чем меньше вязкость жидкости μ.
Рейнольдс объединил эти величины в безразмерный комплекс, который носит название критерия Рейнольдса (Re):
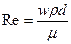
Критерий Re является мерой соотношения между силами вязкости и инерции в движущемся потоке.
Переход от ламинарного к турбулентному движению характеризуется критическим значением Рейнольдса (Reкр)
При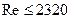 
режим движения устойчиво ламинарный;
При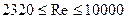 
режим движения неустойчиво турбулентный (переходный);
При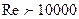 
режим движения устойчиво турбулентный (развитый).
Основные уравнения гидродинамики
1. Уравнение неразрывности (сплошности) потока
В интегральной форме принимает вид: Wρ S = const. (см. модуль 1).
2. Уравнения Навье-Стокса
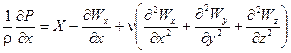
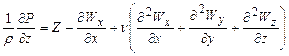
Частные случаи уравнения Навье-Стокса
1. Жидкость находится в покое (равновесии), т. е. Wx = Wy = Wz = 0
получим дифференциальные уравнения равновесия Эйлера
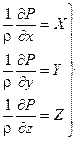– дифференциальные уравнения Эйлера
Проинтегрируем и получаем: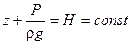 
- основное уравнение гидростатики.
2. Движение идеальной жидкости
Идеальная жидкость – жидкость, которая не изменяет объема при изменении давления и температуры, а также не обладает вязкостью, то есть несжимаема.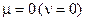 
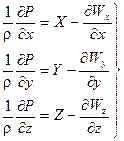– получили дифференциальные уравнения движения Эйлера
Проинтегрируем: 
– уравнение Бернулли для идеальной жидкости.
|
|
|
|
|
|
