 |
Моделирование химико-технологических процессов
|
|
|
|
Моделирование химико-технологических процессов
Наиболее перспективный метод решения задач исследования и расчета БТ процессов – теоретический метод, основанный на составлении и решении дифференциальных уравнений, полностью описывающих процесс. Дифференциальные уравнения описывают целый класс однородных явлений.
Различают два метода моделирования
Принципиального различия между этими методами нет, поскольку оба они в большей или меньшей степени основаны на экспериментальных данных и различаются лишь подходом к их обработке и анализу.
I Метод численного эксперимента (математическое моделирование) представляет собой систему уравнений математического описания, отражающую сущность явлений, протекающих в объекте моделирования, которая с помощью определенного алгоритма позволяет прогнозировать поведение объекта при изменении входных и управляющих параметров. Применяют в тех случаях, когда неясна физическая сущность процесса.
Общая схема математического моделирования:
1. Постановка задачи;
2. Анализ теоретических основ процесса (составление физической модели процесса);
3. Составление математической модели процесса;
4. Алгоритмизация математической модели (выбор метода ее решения);
5. Параметрическая идентификация модели (здесь необходимо подобрать коэффициенты, которые учитывают те или иные особенности объекта);
6. Проверка адекватности математической модели (степень приближения данных по модели к экспериментальным данным);
7. Решение на ЭВМ математической модели;
8. Анализ полученной информации.
II Метод обобщенных переменных (физическое моделирование), в основе которого лежат теория подобия. Подобие – это условие, при котором возможен количественный перенос результатов опыта с модели на оригинал.
|
|
|
Основной принцип метода – выделение подобных явлений.
Различают следующие виды подобия:
1. Геометрическое подобие предполагает, что сходственные размеры натуры и модели подобны, а их отношение выражается постоянной величиной:
Безразмерную величину ае называют константой геометрического подобия или масштабным (переходным) множителем. Константа подобия позволяет переходить от размеров одной системы (модели) к размерам другой (натуры).
2. Временное подобие предполагает, что сходственные точки или части геометрически подобных систем (натуры и модели) проходят геометрические подобные пути в промежутки времени, отношение которых является постоянной величиной:
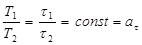, где Т1, Т2 – время прохождения сходственными частицами всего аппарата, соответственно натуры и модели; τ 1, τ 2 – время прохождения сходственными частицами подобных путей; – константа временного подобия.
3. Подобие физических величин предполагает, что в рассматриваемых подобных системах отношение значений физических величин двух любых сходственных точек или частиц, подобно размещенных в пространстве и времени, есть величина постоянная.
, 
, 
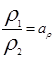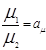4. Подобие начальных условий предполагает, что начальное и граничное состояние системы подобны.
Инварианты и критерии подобия
Если все сходственные величины, определяющие состояние данной системы и системы ей подобной, выразить в относительных единицах, то эти отношения будут величиной постоянной.
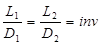– безразмерные числа, выражающие отношение однородных величин, в подобных системах, носят название инвариантов подобия ;
Инварианты подобия, представляющие отношения однородных величин, называются симплексами или параметрическими критериями. Инварианты подобия, выражающие отношение разнородных величин, называются критериями подобия
|
|
|
Равенство критериев подобия – единственное количественное условие подобия процессов (тепловых, диффузионных и др. ).
Если константы подобия найдены из условий однозначности, то образованные из них критерии подобия называются определяющими. Критерий, в который входит искомая величина, называют определяемым.
Любая зависимость между переменными может быть выражена в виде зависимостей между критериями подобия: f(k1, k2……ki) = 0. Эту зависимость называют обобщенным (критериальным уравнением), а критерии k1, k2……ki – обобщенными переменными.
(Обычно это уравнение записывают в виде зависимости определяемого критерия подобия от определяющих):
К1 = f(k2, k3.. ), например 
, где А, n, m – постоянные множители, полученные из экспериментальных данных.
|
|
|
