 |
Преобразование дифференциальных уравнений
|
|
|
|
Преобразование дифференциальных уравнений
Критерии подобия можно получить путем преобразования дифференциальных уравнений, по следующей схеме:
1. записывают дифференциальное уравнение, описывающее исследуемый процесс;
2. делят все слагаемые дифференциального уравнения на какое-нибудь одно, в результате чего получают безразмерный комплекс;
3. отбрасывают знаки дифференциалов, при этом, символы, показывающие степени дифференциалов, сохраняют.
Указанная схема получения критериев подобия из дифференциальных уравнений применяется во всех разделах курса.
Рассмотрим, например, гидродинамическое подобие.
Перенос импульса: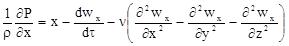 
1 2 3 4
1. 
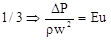- Критерий Эйлера, характеризует отношение силы гидростатического давления к силам инерции в подобных системах.
2. x = -g, 
- Критерий Фруда, характеризует отношение силы тяжести к силе инерции.
3. 
- Критерий Рейнольдса, характеризует отношение сил инерции и сил трения и определяет режим движения всех точек в подобных системах.
Т. о. решение дифференциального уравнения может быть представлено критериальным уравнением вида: f (Eu, Fr, Re) = 1 – Обобщенное критериальное уравнение;
В нем определяемым является критерий Эйлера, т. к. при решении практических задач с помощью этого уравнения определяют величину Δ Р. Критерии Рейнольдса и Фруда – определяющими, так как они составлены из величин, выражающих условия однозначности. Тогда это уравнение можно представить в виде:
Eu = f (Re, Fr).
Возникают вопросы:
1. Какие параметры необходимо измерить?
2. Как представлять полученные данные?
3. Как и где применять?
Ответы:
1. Те, которые входят в критерии подобия, характеризующие данный процесс;
|
|
|
2. Представлять в виде критериальных уравнений;
3. В подобных процессах.
Самостоятельно:
1. Отличие физического и математического моделирования.
2. Этапы математического моделирования.
3. Метод анализа размерностей.
Лекция №5
Технико-экономическая оценка эффективности химико-технологических и биотехнологических процессов.
Оптимизация ХТ процессов
Конечной целью и главной целью моделирования является определение наилучших, оптимальных условий протекания процесса. Решение данной задачи предполагает ее формализацию, что позволяет определить алгоритм решения и обеспечивает условия для применения ЭВМ.
Оптимизация состоит из трех основных этапов:
1. формулирование задачи оптимизации;
2. определение оптимальных условий протекания процесса;
3. внедрение оптимальных условий в производство.
Схематично любой процесс, исходя из внешних признаков, можно представить следующим образом:
Схематичное изображение процесса
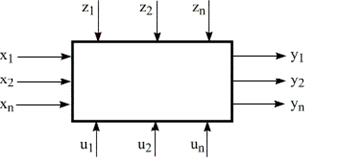
Обычно выделяют следующие группы:
1. Входные параметры Хi. Их значения можно измерить, но на них нельзя воздействовать (состав исходного сырья, который не поддается регулировке).
2. Управляющие параметры Ui. Параметры, на которые можно оказывать прямое воздействие (количество исходной смеси, давление, температура и т. д. ).
3. Возмущающие параметры Zi. Их значение случайным образом изменяются, но не доступны для измерения (примеси в исходном сырье, изменение активности катализатора).
4. Выходные параметры Yi. Параметры, величина которых определяется режимом процесса (характеристика получаемой продукции: t смеси на выходе, себестоимость и т. д. )
Оптимизирующие воздействия (оптимизирующие факторы ОФ ) – это те входы системы, с помощью которых мы воздействуем на нее в процессе оптимизации. То есть – управляющие параметры. Обычно выбирают те входы, которые наиболее существенно влияют на процесс и изменять которые наиболее просто. Так, на стадии проектирования процесса в число оптимизирующих факторов целесообразно включить размеры аппарата. Если же оптимизируется действующая установка, то размеры аппарата заданы и изменять их не стоит.
|
|
|
Критерий оптимальности КО (параметр оптимизации) – это та входная величина, значение которой кладется в основу оценки процесса при выборе его оптимальных показателей. Критерием оптимальности не может служить любая входная величина.
Требования к критерию оптимальности:
1. Критерий оптимальности должен быть единственным;
2. Критерий оптимальности должен выражаться числом;
3. Критерий оптимальности должен обладать следующим свойством: «Оценка качества процесса должна изменяться монотонно с изменением критерия оптимальности». Т. е. критерием оптимальности не может служить величина, имеющая некоторое оптимальное значение.
Признаком оптимального решения является достижение экстремума критерия оптимальности. Например, чем больше производительность установки, тем лучше.
Трудность выбора критерия оптимальности состоит в том, что из всех выходных показателей процесса нужно выбрать главный.
В качестве критерия оптимальности могут выступать:
а) технологические параметры (выход продукта, качество, скорость процесса);
б) конструктивные характеристики (высота, диаметр… аппарата);
в) экономические параметры (себестоимость, прибыль);
г) технико-экономические параметры.
Наиболее обоснованными являются экономические критерии оптимальности.
Важная особенность задач оптимизации – наличие ограничений (ограничивающих факторов). Типичными ограничениями являются: ограничения по количеству, по качеству, ограничения по экономическим соображениям и техническим условиям.
Количественно структура ограничений может быть двух типов:
1. ограничения типа равенства 
, (1)
Например, производительность аппарата может быть точно задана.
2. ограничения типа неравенства 
(2)
|
|
|
Например, t не должна быть выше предела, при котором нарушается прочность конструкционных материалов.
|
|
|
