 |
Математическое обеспечение сапр
|
|
|
|
СИСТЕМ ОБСЛУЖИВАНИЯ
Введение в тему
Математическое обеспечение САПР содержит математические модели, методы и алгоритмы проектируемых объектов. Модель является представлением объекта в некоторой форме, отличной от формы его реального существования и отражающей его наиболее существенные свойства. Исследование свойств объекта с помощью модели называется моделированием. Математические модели представляют собой математическое описание физических объектов, явлений и процессов, выражающее внутренние законы их динамики, взаимодействие с внешней средой и другие свойства. При функционировании систем обслуживания приходится решать задачи различного плана: обеспечение качества обслуживания, качества выпускаемой продукции (выполняемой услуги), эффективности работы (получение максимальной прибыли) и др. Следовательно, при проектировании СО необходимо иметь соответствующее математическое обеспечение.
Задачи систем массового обслуживания
Важная задача моделирования систем – обеспечение синхронной и сбалансированной работы всех ее элементов. Для моделирования реальных систем обслуживания используется теория массового обслуживания (ТМО).
ТМО занимается изучением процессов, связанных с массовым обслуживанием. Цель ее не изучение какого-либо конкретного процесса обслуживания, а разработка методов решения типовых задач, пригодных к использованию в различных областях человеческой деятельности.
Практические задачи ТМО связаны с исследованием любых операций, состоящих из многих однородных элементарных операций. Системы массового обслуживания (СМО) предназначены для многократного проведения некоторой однотипной элементарной операции, которую называют операцией обслуживания. При обслуживании очень важно качество обслуживания и как это обслуживание организованно.
|
|
|
Улучшить организацию обслуживания можно методом проб, путем проведения экспериментов, но это связано иногда с большими материальными затратами, опасностью для здоровья, а иногда просто невозможно провести эксперимент. ТМО позволяет использовать математический аппарат для оценки явлений и процессов, имеющих характер массового обслуживания, не прибегая к проведению экспериментов.
Работа любой СМО состоит в выполнении поступающего на нее потока требований или заявок. Заявки поступают одна за другой в некоторые случайные моменты времени. Каждая СМО в зависимости от числа каналов и их производительности обладает конкретной пропускной способностью. Под пропускной способностью обычно понимают среднее число заявок, которое система может обслужить в единицу времени.
Задача ТМО – установить зависимость между характером потока заявок, производительностью отдельного канала, числом каналов и эффективностью обслуживания. Всякая задача теории массового обслуживания считается решенной, если определены количественные характеристики качества функционирования системы обслуживания.
Для полного описания СМО и постановки задачи исследования необходимо определить структуру системы, дисциплину обслуживания и показатели качества обслуживания. Качество обслуживания тем выше, чем больше число обслуживающих единиц, но экономически невыгодно иметь лишние обслуживающие единицы. Поэтому возникает задача оптимизации: определить количество обслуживающих единиц, обеспечивающее требуемый уровень качества обслуживания.
Основные понятия теории массового обслуживания
Случайные процессы в СМО. В СМО заявки поступают в случайные моменты времени, число заявок случайно и случайна длительность обслуживания каждой заявки, поэтому процессы в СМО являются случайными дискретного типа с непрерывным временем.
|
|
|
СМО можно представить в виде физической системы дискретного типа или с конечным множеством состояний  Переход системы из одного состояния в другое осуществляется скачком в тот момент времени, когда происходит одно из событий:
Переход системы из одного состояния в другое осуществляется скачком в тот момент времени, когда происходит одно из событий:
· приход заявки;
· освобождение канала;
· уход заявки из очереди;
· и др.
Так как в СМО переход из состояния в состояние возможен в любой момент времени, то случайный процесс дискретного типа будет с непрерывным временем и обратными переходами (занятый канал может освободиться, очередь может исчезнуть).
Рассмотрим 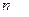 канальную СМО, в которой поступившая заявка при занятости
канальную СМО, в которой поступившая заявка при занятости 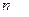 каналов, покидает систему не обслуженной. Это система с
каналов, покидает систему не обслуженной. Это система с 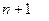 возможными состояниями:
возможными состояниями:
· 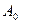 - все каналы свободны;
- все каналы свободны;
·  - один канал занят;
- один канал занят;
·
· 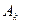 -
-  каналов заняты;
каналов заняты;
·
· 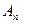 - все каналы заняты.
- все каналы заняты.
Изобразим схему возможных переходов из состояния в состояние (рис.4.1).

Рис.4.1. Схема возможных переходов
Стрелка над изображением состояния указывает, что система остается в этом состоянии. Стрелки на схеме между состояниями указывают на возможность переходов из состояния в состояние. Перескоков через состояния нет, так как предполагается, что одновременно две заявки не приходят.
Поток событий (заявок, требований) или входящий поток вызовов. Потоком событий называется последовательность однородных событий, которые происходят одно за другим в случайные моменты времени. За начальный момент времени принимают 
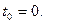 Процесс поступления заявок является случайным, поэтому входящий поток может быть описан некоторой случайной функцией
Процесс поступления заявок является случайным, поэтому входящий поток может быть описан некоторой случайной функцией 
 , характеризующей число поступивших заявок на интервале времени
, характеризующей число поступивших заявок на интервале времени 
 . Число заявок – целое неотрицательное число, поэтому функция
. Число заявок – целое неотрицательное число, поэтому функция  может принимать только целочисленные неотрицательные значения в любое время
может принимать только целочисленные неотрицательные значения в любое время 
 . С ростом
. С ростом 
 не убывает. Для описания функции
не убывает. Для описания функции  достаточно знать вероятность того, что за время
достаточно знать вероятность того, что за время 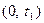 поступит
поступит  заявок, за время
заявок, за время 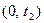 -
-  заявок и т.д. Вероятность полностью определяет поток заявок, но ее сложно определить. На практике встречаются потоки, которые можно проще описать. К таким потокам относится простейший поток событий.
заявок и т.д. Вероятность полностью определяет поток заявок, но ее сложно определить. На практике встречаются потоки, которые можно проще описать. К таким потокам относится простейший поток событий.
|
|
|
|
|
|


