Главная | Обратная связь | Поможем написать вашу работу!

Простейший поток и его свойства

Обычно входящий поток заявок является простейшим. Он обладает тремя свойствами: стационарностью, отсутствием последействия и ординарностью.

Свойство стационарности означает, что вероятностный режим потока не должен меняться во времени. Поток заявок называется стационарным, если вероятность попадания заявок на участок времени зависит лишь от длины участка и не зависит от сдвига 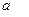вдоль оси времени. Существует понятие плотность или интенсивность потока – это среднее число заявок, приходящихся на единицу времени или математическое ожидание числа заявок, поступающих за единицу времени. Для стационарного потока плотность потока постоянна.

Отсутствие последействия означает, что заявки поступают в систему независимо друг от друга. Поток заявок называется потоком без последействия, если число заявок, поступивших в систему после момента времени , не зависит от числа заявок, поступивших в систему до момента времени . Обычно входящий поток – поток без последействия, а выходящий – с последействием. Например, входящий поток пассажиров является поток без последействия, так как пассажиры приняли решение ехать независимо друг от друга, а выходящий поток – с последействием, так как пассажиры прибыли на одном поезде, автобусе и т.д.

Свойство ординарности означает, что заявки приходят в систему поодиночке, а не парами, тройками, т.е. считается, что практически невозможно поступление двух и более заявок в один и тот же момент времени.

Основная задача простейшего потока – найти вероятность поступления заявок на интервале так как на интервал либо не поступит ни одной заявки, либо поступит одна, либо две и т.п. (одно из событий обязательно должно произойти, но совместно события не могут появиться).

Случайная величина , равная числу поступивших заявок за время , имеет закон распределения Пуассона.

где - плотность потока. Плотность полностью определяет простейший поток, т.е. среднее число заявок, поступивших за время , равно .

Простейший поток заявок одновременно обладает свойствами стационарности, ординарности и отсутствия последействия. Рассмотрим на оси простейший поток заявок как последовательность случайных точек (рис.4.2).

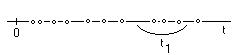
Рис.4.2. Схема простейшего потока заявок

Выделим произвольный участок времени длиной 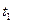. Для простейшего потока число заявок, попадающих на участок 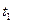, распределено по закону Пуассона с математическим ожиданием .

В соответствии с законом Пуассона:

· вероятность того, что за время 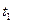поступит ровно заявок, равна

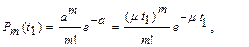
· вероятность того, что на участок длиной 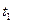не попадет ни одной заявки, т.е. участок окажется пустым, будет равна

· вероятность того, что на участок 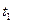попадет хотя бы одна заявка, равна

Таким образом, если исследуемый поток является простейшим, то для его полного описания достаточно вычислить математическое ожидание числа заявок, поступивших за единицу времени.

Четвертое свойство простейшего потока – вероятность поступления в течение промежутка времени длительности ровно заявок принимает наибольшее значение в момент времен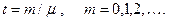и При максимумы будут в моменты времени 0, 1, 2, … (рис.4.3).

Рис.4.3. Иллюстрация 4-го свойства простейшего потока

Параметр любого стационарного потока. Для любого стационарного потока существует предел 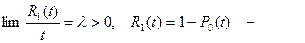вероятность поступления в систему за время по крайней мере одной заявки, вероятность не поступления заявки на интервале времени , - параметр стационарного потока. Для простейшего потока параметр потока равен плотности потока для других стационарных потоков На практике часто принимают что означает ординарность потока.

Существует теорема Королюка. Для любого стационарного потока с конечной плотностью необходимым и достаточным условием ординарности потока является равенство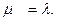

Основные формулы простейшего потока:

· Параметр потока равен плотности

· Вероятность поступления заявок на интервал времени длины

· Вероятность того, что на интервал времени не поступит ни одной заявки

· Вероятность того, что на интервал времени поступит по крайней мере одна заявка

· Среднее число заявок, поступивших на интервал времени

Простейший поток играет среди потоков событий особую роль. Можно доказать, что при взаимном наложении (суммировании) большого числа ординарных, стационарных потоков с любым последействием получается поток очень близкий к простейшему. Обычно достаточно сложить 4-5 потоков, чтобы получить поток со свойствами простейшего потока.

Пример 4.1. В аварийную службу поступают вызовы с плотностью =2 вызова в сутки. Считая, что входящий поток вызовов является простейшим, определить вероятность того, что за =15 часов:

· не поступит ни одного вызова;

· поступит хотя бы один вызов;

· поступит ровно два вызова;

· поступит ровно три вызова;

· поступит ровно четыре вызова;

· поступит один или два вызова;

· поступит более двух вызовов.

Кроме того, проверить четвертое свойство простейшего потока вызовов.

Решение выполняем в следующей последовательности:

1. Определяем плотность вызовов в час. В данном случае имеем

2. Определяем среднее число заявок

3. Последовательно рассчитываем в среде электронных таблиц (ЭТ) требуемые вероятности по формулам:

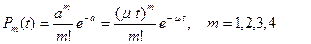
· вероятность того, что за 15 часов будут поступать один или два вызова, равна сумме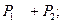

· вероятность того, что за 15 часов поступит более двух вызовов, определяется по формуле

Расчет при =15 является контрольным.

4. Определяем время достижения вероятностью своего максимального значения в соответствии с 4-м свойством простейшего потока заявок -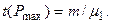

5. Выполняем расчет вероятностей, приведенных в пункте 3, для построения графиков вероятностей, иллюстрирующих четвертое свойство простейшего потока заявок.

Расчетные формулы представлены в таблице 4.1, результаты расчета – в таблице 4.2 и на рис. 4.4.

Таблица 4.1. Расчетные формулы

	A	B	C	D	E	F	G
		t		a
			=a2/24	=c2*b2	=exp(-d2)	=1-e2

		P(t)=	=*
			=c3/$c$2
			=d4+e4		=1-(c4+c6)
	t	a
		=$c$2*a8	=*

…

Примечания. 1. В ячейку С4 записана формула =$d$2^c3*exp(-$d$2)/ФАКТР(c3), в ячейку С8 - =$b8^c$3*exp(-$b8)/ФАКТР(c$3).

1. Стрелки и означают копирование в эти ячейки.

Таблица 4.2. Результаты расчета

Рис.4.4. Иллюстрация 4-го свойства простейшего потока

Анализ результатов. Полученные результаты позволяют сделать некоторые предварительные выводы. Вероятность того, что в течение 15 часов поступит:

¨ хотя бы один вызов

¨ один или два вызова

¨ более двух вызовов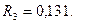

Следовательно, через каждые 15 часов можно ожидать один-два вызова на выполнение аварийных работ. Более чем два вызова в среднем будут поступать в 13 случаях из ста. На основе этого можно предположить численный состав аварийной службы в данном случае, т.е. при плотности потока 2 вызова в сутки.

Пример 4.2. В качестве входящего потока рассматривается поток, состоящий из заявок на обслуживание станков. Станок остановился - поступила заявка на обслуживание. Обслуживание состоит в устранении причины остановки станка. Поток заявок на обслуживание станков является простейшим и имеет плотность =0,5 заявок в час. Рассчитать вероятность отказа в течение времени 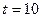ч различного количества станков (.Построить график этой вероятности.

Размещение информации представлено в таблице 4.3. Результаты решения приведены на рис. 4.5 и в таблице 4.4.

Пример 4.3. Поток, состоящий из заявок на обслуживание станков, является простейшим. Среднее время обслуживания одного станка =12 мин. Определить вероятность того, что за время остановится не меньше двух станков. Рассчитать вероятность того, что за время остановится 2, 3, …, 6 станков. Плотность потока заявок на обслуживание взять из примера 4.2. Построить соответствующий график.

Размещение информации представлено в таблице 4.3. Результаты решения приведены на рис. 4.6 и в таблице 4.4.

Таблица 4.3. Размещение информации

A	B	C	D	E	F	G	H	I
	t	a
0,5		=a2*b2
m=
P(t)=	=*
								R₇
								=1-i4
Т_об,мин	Т_об, ч	a
	=a8/60	=a2*b8
m
P(Т_об)=	=*

Примечание. В ячейки В4 и В10 соответственно записаны формулы: =$c$2^b3*EXP(-$c$2)/ФАКТР(b3); =$c$8^b9*EXP(-$c$8)/ФАКТР(b9).

Таблица 4.4. Результаты расчета

Анализ результатов расчета. Наиболее вероятно, что после 10 часов работы потребуют обслуживание 4 или 5 станков (рис.4.5). Более 6 станков могут потребовать обслуживание в 24 случаях из ста, так как =0,2378. Вероятность того, что за 12 мин обслуживания остановится не меньше двух станков, равна т.е. вероятность эта мала. Следовательно, можно надеяться, что за это время остановится один станок или ни одного.

Рис.4.5. Вероятность остановки различного количества станков

в течение 10 часов

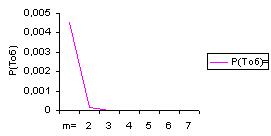
Рис.4.6. Вероятность того, что за12 мин времени обслуживания

остановится не меньше двух станков

⇐ Предыдущая 1 2 345 6 7 8 Следующая ⇒

Воспользуйтесь поиском по сайту: