Модели задач математического программирования

Разработка плана производства и реализации продукции является важной задачей плановой деятельности предприятий. Каждое предприятие должно уметь составлять наиболее целесообразный и всесторонне обоснованный план своей деятельности, что обеспечивается путем построения и реализации математических моделей задач оптимизации. Возможны различные варианты постановки задач, определяемые конкретными производственно-хозяйственными ситуациями каждого предприятия. Однако подходы к постановке задач и построению моделей являются общими для любых предприятий и сводятся в принципе к следующему:

· составляется список всех ресурсов, которые могут выступать в математических моделях задач оптимизации в качестве ограничений;

· отбираются виды продукции (ассортимент) и характеристики каждого вида (цена, себестоимость, прибыль, отнесенные к единице продукции, нормы расхода ресурсов на изготовление единицы продукции).

Нормы расхода учитываются при составлении ограничений, а цена, прибыль, себестоимость при построении критерия оптимизации.

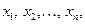Постановка общей задачи. Найти значения переменных (параметров) которые удовлетворяют ограничениям (уравнениям или неравенствам)

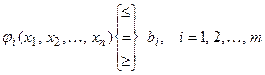(4.13)

граничным условиям 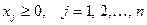(4.14)

и доставляют экстремум (max или min) целевой функции

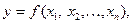(4.15)

где 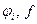– известные функции; 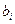- заданные константы. Значения и не связаны между собой.

Всякий набор управляемых переменных 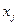, удовлетворяющий ограничениям и граничным условиям, определяет допустимое решение (допустимый план). Допустимое решение, при котором достигается экстремум целевой функции, называется оптимальным.

Если ограничения (4.13) и целевая функция (4.15) линейны, то такие задачи относятся к задачам линейного программирования (ЛП). Если хотя бы одно ограничение или целевая функция содержат 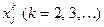или произведение управляемых переменных, то имеем задачу нелинейного программирования.

Математическая модель задачи оптимизации содержит три составляющие: целевую функцию, ограничения и граничные условия. Граничные условия определяют предельно допустимые значения управляемых переменных 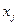. Ограничения устанавливают зависимости между управляемыми переменными. Целевая функция показывает, в каком смысле решение должно быть наилучшим.

Рассмотрим постановки и математические модели некоторых производственных задач.

4.7.1. Оптимизация производственного плана предприятия

Постановка задачи. Предприятие может выпускать типов продукции, для производства которых имеется 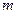видов ресурсов. Известны: 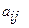- затраты 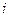- го вида ресурса на производство единицы продукции - го типа 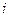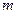( =1, 2,…, ; =1, 2,…, ); 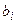- полные объемы имеющихся ресурсов на период планирования; 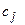- прибыль, получаемая предприятием от производства и реализации единицы продукции - го типа. Маркетинговые исследования показали, что спрос на ассортимент выпускаемой предприятием продукции не ограничен.

Требуется составить такой план выпуска продукции, который технологически осуществим по наличию имеющихся ресурсов и приносит предприятию максимальную прибыль.

Для удобства составления математической модели исходные данные сведем в таблицу 4.10.

Таблица 4.10. Сводка исходных данных

Виды ресурсов	Типы продукции	Объемы ресурсов на период планирования
		…		…
		…		…
			…		…
			…		…
…	…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…	…
			…		…
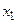
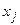
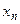
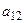
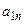
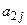
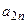
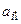
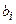
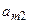
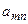
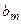
Прибыль от единицы продукции			…		…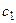

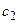
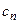
Обозначим план выпуска продукции через