 |
1. 4. Математическая обработка результатов исследований
|
|
|
|
1. 4. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЙ
Математическая обработка полученных данных проводится с помощью параметрических методов. Определяются следующие параметры: средняя арифметическая, среднее квадратичное отклонение, ошибка средней арифметической. Достоверность различий полученных результатов оценивается с помощью t-критерия Стьюдента (Лакин Г. Ф., 1980; Чиженок Т. М., Муравська Г. О., 2000).
1. Вычисление средней арифметической.
Средняя арифметическая величина вычисляется путем сложения всех полученных значений (вариант), а затем деления полученной суммы на число значений (n).
Вычисление средней арифметической проводят по формуле:
= 
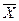, (1)
где 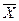– средняя арифметическая,
X1 , Х2, Х3 … - полученные значения вариант (Хί ),
n - общее число значений,
∑ - знак суммирования значений от первого до последнего.
Например:
нам дано 5 значений Хί = 11, 12, 13, 14, 15, тогда n = 5.
Среднее значение будет равно =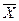 
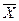= 13, 0
2. Вычисление среднего квадратичного отклонения.
Дополнительной характеристикой средней арифметической, показывающей вариативность признака, является среднее квадратичное отклонение (δ ). Чем меньше δ, тем более однородным будет вариационный ряд, т. е. более стабильные признаки, показатели, результаты.
Среднее квадратичное отклонение используется при оценке изменчивости вариационного ряда, вычислении коэффициента вариации, вычислении ошибки средней арифметической.
Существует простейший метод вычисления среднего квадратичного отклонения по формуле:
|
|
|
δ = 
(2)
где Хmax – наибольшее значение варианты;
Хmin - наименьшее значение варианты;
К - коэффициент количества случаев.
Например:
из приведенного ряда значений Xί = 11, 12, 13, 14, 15 видно, что наибольшее значение Хmax = 15, 0, наименьшее значение Хmin = 11, 0. Коэффициент К по таблице для n = 5 равен 2, 33 (см. приложение 12). Подставляем в формулу значения и вычисляем среднее квадратичное отклонение:
δ =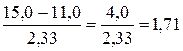 
δ = 1, 71
Принято считать, что все индивидуальные показатели в пределах ± 1 δ оцениваются как «норма» и носят случайный характер. Показатели ± 2 δ носят неслучайный характер, а показатели ± 3 δ имеют значительное отклонение от нормы.
3. Вычисление ошибки средней арифметической проводят по формуле:
(3)
В знаменателе формулы ставится n-1 в том случае, когда n< 30, если значений больше 30, то ставится n.
Ошибка средней арифметической (±SX) используется при вычислении достоверности t.
Например:
для данного ряда значений Xί = 11, 12, 13, 14, 15 δ = 1, 71
± 
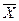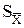= 13, 00 ± 0, 86
4. Вычисление достоверности различий между двумя средними с помощью t – критерия Стьюдента.
При определении эффективности методик исследования обычно сравнивают результаты экспериментальной и контрольной групп, различия между которыми должны быть статистично доказанными. Для этого рассчитывается коэффициент достоверности (t) по формуле:
t факт. =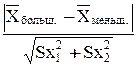 
, (4)
где 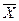больш. – большее значение средней арифметической,
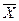меньш. – меньшее значение средней арифметической.
Достоверность различий обозначается буквой «Р» со знаком «меньше» (< ) или «больше» (> ). Достоверные значения находятся в интервале от 95, 0 % до 99, 9 % и обозначаются Р≤ 0, 05; Р≤ 0, 01; Р≤ 0, 001.
|
|
|
Полученное t факт. сравнивают с tтабл. (приложение 14).
Например:
мы вычислили среднее арифметическое и ошибку средней арифметической для двух групп:
контроль 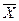1± 
= 75, 9 ± 2, 7, n1 = 7,
эксперимент 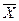2±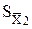 
= 89, 3± 2, 1, n2 = 7
Находим t фактическое (t факт )
t факт = 
Находим по таблице (приложение 7) для К= n1 + n2 - 2 = 12
tтабличное и сравниваем с t фактическим.
tтабл = 3, 05
Поскольку t факт. > tтабл разница между средними арифметическими контрольной и экспериментальной групп достоверна, Р≤ 0, 01.
|
|
|
