 |
14. Что такое линия наибольшего наклона (ската) плоскости?
|
|
|
|
14. Что такое линия наибольшего наклона (ската) плоскости?
Прямая, принадлежащая плоскости и перпендикулярная к горизонтали (фронтали или профильной прямой) - второй вид главных линий плоскости, получила название линия наибольшего наклона плоскости к плоскости проекции H (V и или W). Иногда линию наибольшего наклона к плоскости H называют линией наибольшего ската.
Отличительным признаком для проекции линии наибольшего ската является перпендикулярность ее горизонтальной проекции, горизонтальной проекции горизонтали и горизонтальному следу плоскости α H см. рисунок.
Следует иметь ввиду, что линия наибольшего наклона будет использоваться для определения угла наклона плоскости к плоскостям проекции.
15. Как в общем случае строится линия пересечения двух плоскостей?
Алгоритм построения линии пересечения плоскостей:
1. Проводим вспомогательную плоскость уровня S.
2. Строим линии пересечения плоскости S с заданными плоскостями P и Q –горизонтали h и h1.
3. Определяем точку пересечения построенных прямых h и h1 – точку 1, которая принадлежит обеим плоскостям P и Q.
4. Аналогично определяем точку 2.
5. Соединив точки 1 и 2, получаем линию пересечения заданных плоскостей.
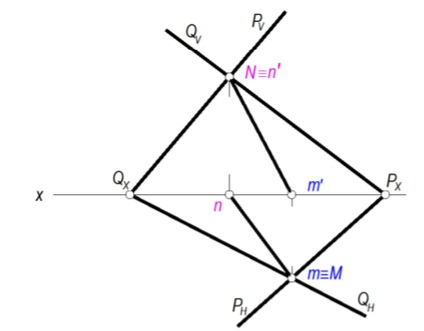
16. Как строится линия пересечения плоскостей, заданных следами?
Линия пересечения плоскостей МН проходит через точки пересечения одноименных следов.
1) Построить линию пересечения плоскостей:
2) Определяем точку пересечения фронтальных следов – N и ее проекции n' и n;
3) Определяем точку пересечения горизонтальных следов – M и ее проекции m и m';
4) Соединяя одноименные проекции точек, получаем линию пересечения заданных плоскостей MN (mn, m'n').
|
|
|
17. Как строится точка пересечения прямой с плоскостью?
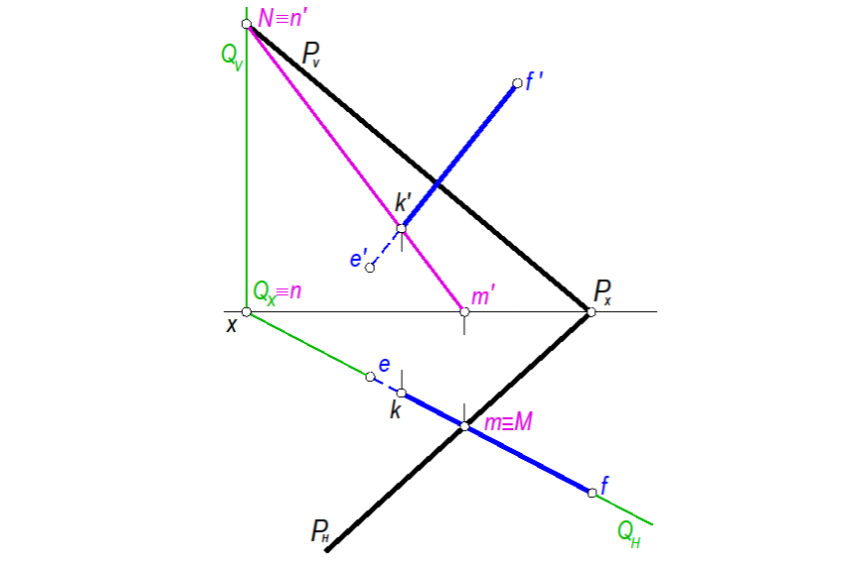Последовательность нахождения пересечения прямой с плоскостью:
1. Через прямую EF проводим посредник (вспомогательную) – проецирующую плоскость S;
2. Находим линию пересечения данной плоскости и посредника – MN;
3. Находим точку пересечения данной прямой EF с линией пересечения плоскостей MN – тоску K.
18. Как строится прямая перпендикулярная плоскости?
| 1. Для того чтобы построить перпендикуляр к плоскости Р(D АВС) через точку D, необходимо сначала построить любую горизонталь в данной плоскости Р(D АВС) – h (h1h2) |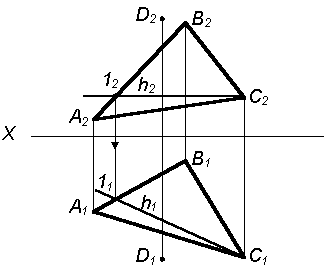 
|
| 2. Строим фронталь в плоскости Р(D АВС) – f ( f1f2) | 
|
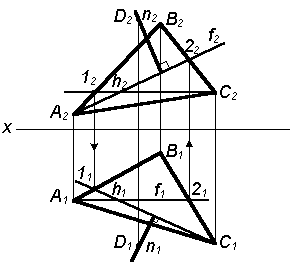
3. Строим перпендикуляр n к плоскости Р(D АВС). Для этого через точку D2 проводим n2, перпендикулярно f2, а через D1 проводим n1, перпендикулярно h1. n (n1n2) ^Р (DАВС), так как n1^h1; h1  P1 ( DА1В1С1) n2^f2; f2 P2 (DА2В2С2)
| 
|
19. Для чего используются преобразования проекций? Какие способы преобразования проекций вы знаете?
Способы преобразования проекций:
1)Способ перемены плоскостей проекций.
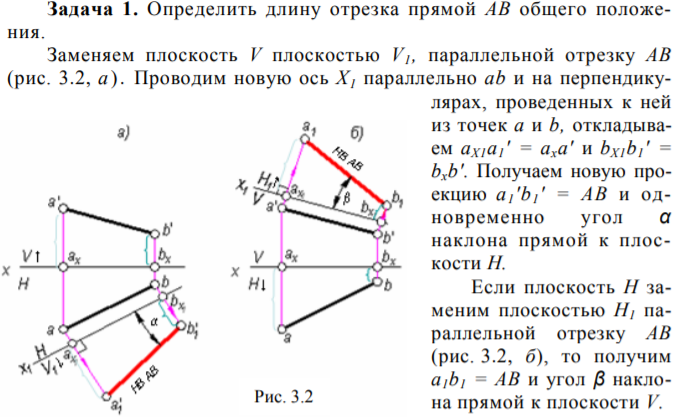
Сущность способа перемены плоскостей проекций состоит в замене одной или двух плоскостей проекций новыми, на которых могут быть получены новые проекции, наиболее удобные для решения конкретной задачи. Количество замен плоскостей и их положение зависят от исходного положения заданной фигуры по отношению к плоскостям проекций и от условий поставленной задачи.
Схема перехода от исходной системы плоскостей проекций к новым системам:
Проследим, как изменятся проекции точки B, если плоскость V заменить на новую плоскость проекций V1 (рис. 3. 1, а ). Плоскость V1 проводим перпендикулярно плоскости Н, положение которой остается без изменения. Плоскости Н и V1 пересекутся по прямой OX1, определяющей новую ось проекций. В новой системе плоскостей проекций вместо проекций b и b' получим новые проекции b и b1′. Легко убедиться, что расстояние от новой проекции точки b1′ до новой оси OX1 (координата Z) равно расстоянию от заменяемой проекции b' до заменяемой оси OX. Чтобы перейти от пространственного чертежа к эпюру, нужно совместить плоскость V1 с плоскостью Н. На эпюре (рис. 3. 1, 6) для построения новой проекции b1′ используем неизменность координаты Z точки B. Для этого достаточно из горизонтальной проекции b провести перпендикуляр к новой оси OX1 и от точки bx1 отложить координату Z, определяемую расстоянием b'bx (ZB) в прежней системе. Замена горизонтальной плоскости Н новой плоскостью Н1 (рис. 3. 1, в) производится аналогично, с той лишь разницей, что теперь не изменяется фронтальная проекция точки b', для построения новой горизонтальной проекции b1 необходимо из сохраняемой фронтальной проекции b' провести линию связи к новой оси OX1 и отложить от новой оси расстояние, равное расстоянию от заменяемой проекции b до заменяемой оси OX. Замена плоскостей проекций может осуществляться только последовательно, нельзя менять обе плоскости сразу.
Основные метрические и позиционные задачи, решаемые способом замены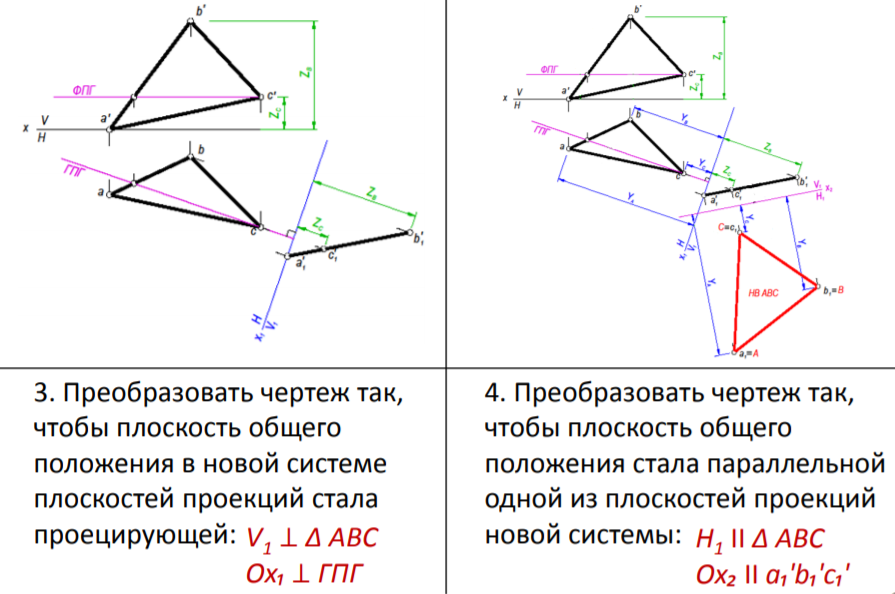 
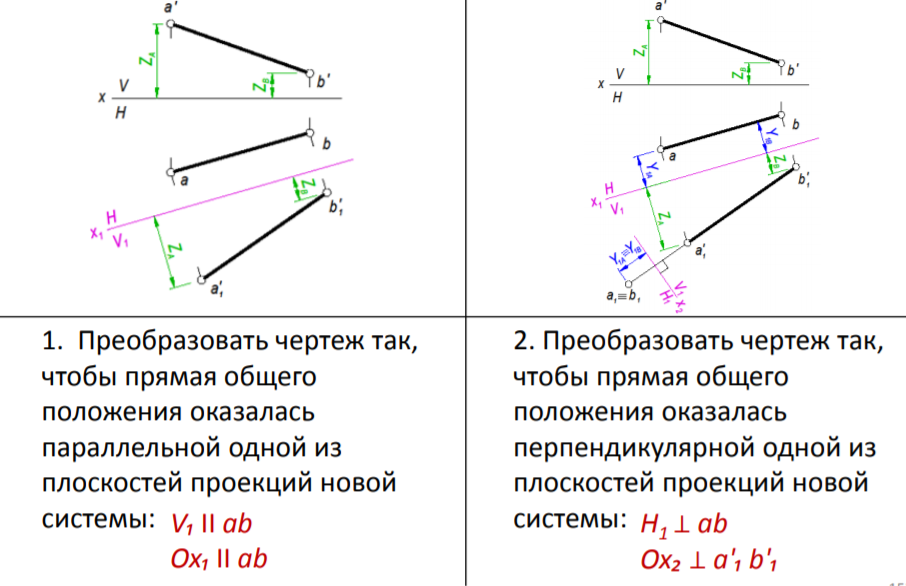плоскостей проекций:
|
|
|
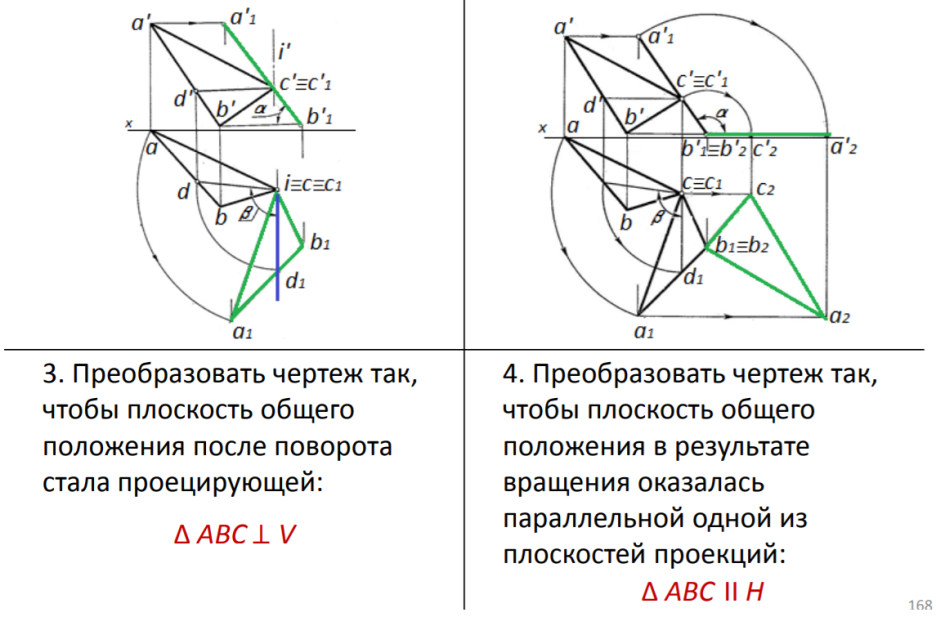2) Способ вращения
Сущность метода: в результате вращения вокруг некоторой оси прямая или плоскость должны занять частное положение относительно неизменной системы плоскостей проекций.
Основные задачи (доп. инфа, на всякий случай, в тетради по проекционке и в методичке этого нет, но в презентации есть):
|
|
|
