Главная | Обратная связь | Поможем написать вашу работу!

2.1) Вращение вокруг линий уровня.

2. 1) Вращение вокруг линий уровня.

2. 2) Способ совмещения

Вращение плоскости вокруг оси, совпадающей с плоскостью проекций, т. е. вокруг следа плоскости, является частным случаем вращения вокруг линии уровня плоскости.

Способ совмещения заключается в том, что заданную плоскость Р вместе с расположенными в ней геометрическими элементами вращают вокруг одного из ее следов РН или РV до совмещения с соответствующей плоскостью проекций Н или V.

Все геометрические элементы (прямые и другие линии, фигуры), лежащие в заданной плоскости, изображаются в натуральную величину на плоскости проекций, с которой производится совмещение. Совмещение позволяет найти величину плоской фигуры по ее проекциям или построить проекции плоской фигуры, лежащей в какой-либо плоскости, по заданным ее размерам.

Если плоскость задана следами, то задача совмещения ее с плоскостью проекций сводится к построению совмещенного положения одного из следов, так как другой след, принимаемый за ось вращения, не меняет своего положения.

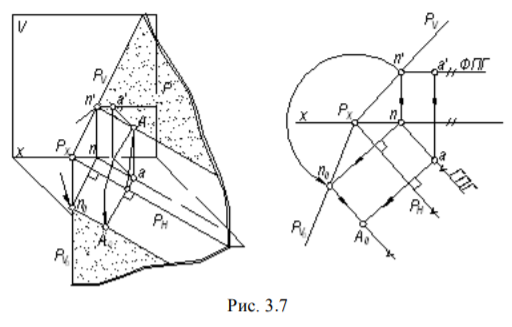
Как видно из рис. 3. 7, для определения совмещенного следа Pv0 при вращении плоскости Р вокруг следа РH достаточно найти совмещенное положение N0 любой точки N следа РV. На рис. 3. 7 показано также совмещение точки А (а, а'), лежащей в плоскости Р, с плоскостью Н при использовании горизонтали.

Задача. Найти натуральную величину треугольника ABC, расположенного в плоскости Р общего положения (рис. 3. 8).

Плоскость Р совмещаем с плоскостью Н вращением вокруг следа РН. Используя горизонталь плоскости, на которых лежат вершины треугольника, находим совмещенные положения В0, С0 этих вершин и получаем треугольник А0В0С0, равный заданному.

20. В чем заключается способ перемены плоскостей проекций?

Сущность способа замены плоскостей проекций состоит в том, что заданную систему плоскостей проекций заменяют новой системой так, что геометрические фигуры оказываются в частном положении относительно новой системы плоскостей проекций.
( Далее для самых смелых, ибо автор сказал, что доп инфа. Берегите свое здоровье! )
Проследим, как изменятся проекции точки B, если плоскость V заменить на новую плоскость проекций V1 (рис а ). Плоскость V1 проводим перпендикулярно плоскости Н, положение которой остается без изменения. Плоскости Н и V1 пересекутся по прямой 0х1, определяющей новую ось проекций. В новой системе плоскостей проекций вместо проекций b и b' получим новые проекции b и b1′. Легко убедиться, что расстояние от новой проекции точки b1′ до новой оси 0х1 (координата Z) равно расстоянию от заменяемой проекции b' до заменяемой оси 0х. Чтобы перейти от пространственного чертежа к эпюру, нужно совместить плоскость V1 с плоскостью Н. На эпюре (рис. 3. 1, 6) для построения новой проекции b1′ используем неизменность координаты Z точки B. Для этого достаточно из горизонтальной проекции b провести перпендикуляр к новой оси 0х1 и от точки bX1 отложить координату Z, определяемую расстоянием b'bx (ZB) в прежней системе. Замена горизонтальной плоскости Н новой плоскостью Н1 (рис. 3. 1, в) производится аналогично, с той лишь разницей, что теперь не изменяется фронтальная проекция точки b', для построения новой горизонтальной проекции b1 необходимо из сохраняемой фронтальной проекции b' провести линию связи к новой оси 0х1 и отложить от новой оси расстояние, равное расстоянию от заменяемой проекции b до заменяемой оси 0х. Замена плоскостей проекций может осуществляться только последовательно, нельзя менять обе плоскости сразу.

21. В чем заключается способ совмещения?
Способ совмещения заключается в том, что заданную плоскость Р вместе с расположенными в ней геометрическими элементами вращают вокруг одного из ее следов Р_Н или Р_V до совмещения с соответствующей плоскостью проекций Н или V.

22. Какие поверхности называются линейчатыми?

Линейчатые поверхности относятся к кривым поверхностям, образованным кинематическим способом

Поверхность, рассматриваемая как непрерывное множество последовательных положений линии, перемещающихся в пространстве по определенному закону. Такой способ образования называется кинематическим. Образующая l перемещается по направляющей m, образуя поверхность. Самые различные формы образующих и направляющих позволяют создать разнообразные поверхности.
Линейчатой называется поверхность, которая может быть образована перемещением прямой линии
К линейчатым поверхностям относятся:
Развертывыемые (Если линейчатая поверхность может быть развернута так, что всеми своими точками она совместится с плоскостью без каких-либо повреждений поверхности (разрывов или складок), то ее называют развертываемой: цилиндрические, конические, с ребром возврата или торсовые).
Неразвертываемые (цилиндроид, коноид, гиперболический параболоид)
С плоскостью параллелизма (Поверхности с двумя направляющими, образующие которых (прямые линии), перемещаясь по этим направляющим, остаются параллельны плоскости, называемой плоскостью параллелизма: цилиндроид, коноид, гиперболический параболоид).
Винтовые (Поверхность, образованная поступательным движением образующей линии вдоль оси и вращательным вокруг оси: прямой геликоид, наклонный геликоид).
Вращения (поверхности образуются вращением прямой линии вокруг оси: прямой круговой цилиндр, прямой круговой 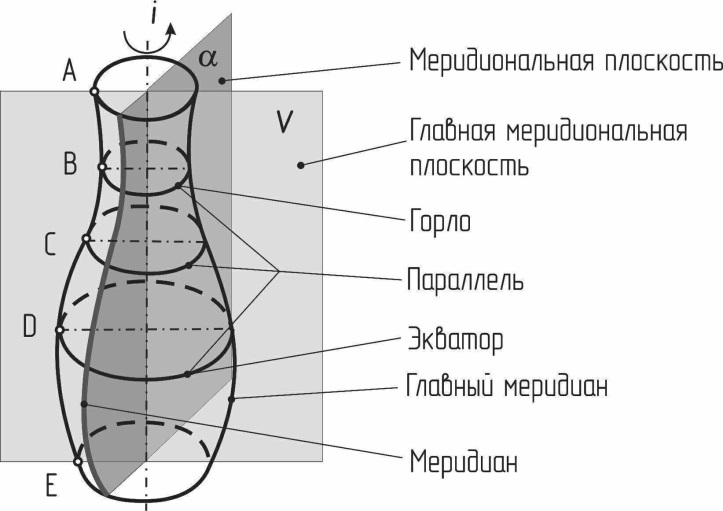конус).

23. Какие поверхности называются поверхностями вращения? Каковы их основные свойства?

Поверхностью вращения называется поверхность, получаемая от вращения какой-либо образующей линии вокруг прямой - оси поверхности. Во многие такие поверхности можно вписать шары с касанием по окружности.
Основные свойства:
1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели. Наибольшую из них называют экватором, наименьшую – горлом.
2. Плоскость, проходящая через ось вращения, меридиональная, пересекает поверхность по двум симметричным относительно оси линиям – меридианам. Плоскость, проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом.

24. Как строится точка на поверхности вращения? Поясните на примере сферической поверхности или конуса.
Поверхностью вращения называется поверхность, образующаяся путем вращения криволинейной или прямолинейной образующей вокруг неподвижной оси.
Принадлежность точки поверхности.
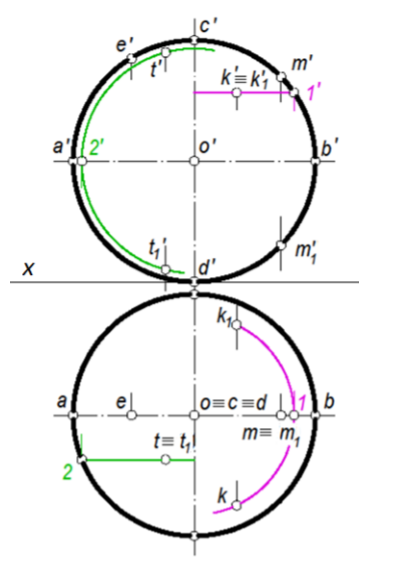
Точка принадлежит поверхности, если она принадлежит какой-либо линии этой поверхности. Чтобы по одной проекции точки построить вторую ее проекцию, необходимо провести линию по поверхности через данную проекцию точки, найти вторую проекцию этой линии и на ней определить недостающую проекцию точки.
Принадлежность точки поверхности сферы.
1)Точки m и e расположены на главном меридиане сферы, их горизонтальные проекции будут находиться на оси ab;
2)через заданные проекции точек к' Ξ к'1 проводим вспомогательную параллель поверхности. Строим вторую проекцию параллели, определяем на ней недостающие проекции к и к1;
3)точки t, t' и t1, t'1 построены аналогично;

25. В чем заключаются проецирующие свойства поверхности? Как они используются при решении позиционных задач?

26. Способ вспомогательных секущих плоскостей.

Построение линии пересечения поверхностей в общем случае осуществляется при помощи вспомогательных секущих поверхностей - посредников. Чтобы найти точки линии пересечения двух поверхностей А и В (рис. 5. 1), проводим вспомогательную поверхность Р и находим линии К и L пересечения поверхностей А и В с поверхностью P. Точки M и N пересечения найденных линий будут искомыми. Проведя несколько вспомогательных поверхностей, найдем требуемое количество точек, определяющих линию пересечения заданных поверхностей.

Вспомогательную поверхность следует выбирать так, чтобы ее линия пересечения с каждой поверхностью проецировалась на плоскости проекций в виде графически простых линий − прямой или окружности.

В качестве вспомогательных поверхностей можно использовать плоскости или сферы. Если в качестве вспомогательных секущих поверхностей используются плоскости, то способ построения называют способом вспомогательных плоскостей. Если используются сферы − способом вспомогательных сфер. Построение линии пересечения поверхностей начинают с определения характерных ее точек − экстремальных (высшей и низшей) и точек видимости, отделяющих видимую часть линии пересечения от невидимой. Видимыми являются те точки, которые принадлежат видимой части как первой, так и второй поверхности. Так, на рис. 5. 2 видимыми на фронтальной проекции линии пересечения будут только те точки, которые принадлежат заштрихованным частям конуса и сферы одновременно.

Порядок построения линии пересечения двух поверхностей:
1. выбирают вид вспомогательных поверхностей;
2. строят линии пересечения вспомогательных поверхностей с заданными поверхностями;
3. находят точки пересечения построенных линий и соединяют их между собою с учетом видимости.

27. Способ вспомогательных секущих сфер.

Для построения линии пересечения поверхностей вместо вспомогательных секущих плоскостей при определенных условиях удобно применять вспомогательные сферические поверхности. При этом могут быть использованы концентрические и эксцентрические сферы.

В отличие от метода вспомогательных секущих плоскостей метод вспомогательных сфер имеет преимущество, так как при построении фронтальной проекции линии пересечения поверхностей не используются две другие проекции пересекающихся поверхностей (рис. 5. 6).

Условия применения способа вспомогательных концентрических сфер для построения линии пересечения двух поверхностей:
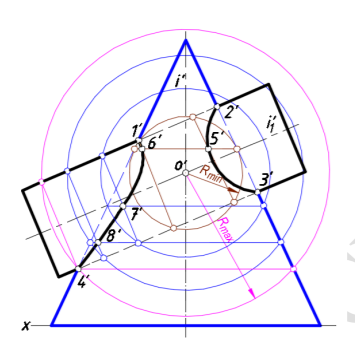1. пересекающиеся поверхности должны быть поверхностями вращения;
2. оси поверхностей вращения должны пересекаться; точка пересечения осей является центром вспомогательных (концентрических) сфер;
3. плоскость, образованная осями поверхностей (плоскость симметрии), должна быть параллельна какой-либо плоскости проекций.

Рассмотрим применение способа вспомогательных концентрических сфер − сфер с постоянным центром для построения линии пересечения цилиндра с конусом вращения (рис. 5. 6).

Прежде всего, отметим четыре общие точки 1′, 2′, 3′, 4′ цилиндра и конуса в пересечении очерковых образующих главных меридианов поверхностей. Оси поверхностей вращения пересекаются в точке О (о′ ), которая является центром вспомогательных сфер. Радиусы сфер изменяются в пределах Rmin ≤ R ≤ Rmах. Пределы радиусов сферических поверхностей находят следующим образом: радиус максимальной сферы определяется расстоянием от центра О до наиболее удаленной точки IV (Rmax = о′ 4′ ), а радиус минимальной сферы определяется как радиус сферы, касающейся одной поверхности (конуса) и пересекающей другую (цилиндр). Каждая сфера пересечет заданные поверхности по окружностям, на пересечении которых и отмечают искомые точки.

Проведем сферу наименьшего радиуса, которая пересечет цилиндр по двум окружностям и коснется конуса. Это сферическое сечение определяет четыре характерные точки линии пересечения, попарно совпадающих (5′, 6′ ) на фронтальной проекции. Введя две вспомогательные сферические поверхности, построили промежуточные точки 7′, 8′ линии пересечения. Соединяя одноименные проекции построенных точек с учетом их видимости, получаем проекции линии пересечения поверхностей.

28. Сформулируйте теорему Монжа. Поясните на примере.

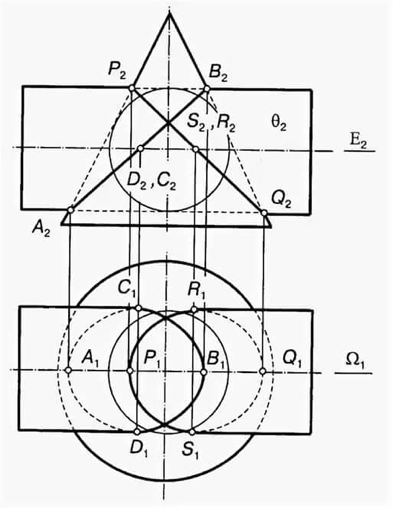Если две поверхности второго порядка описаны около третьей того же порядка, то они пересекаются по двум плоским кривым.

⇐ Предыдущая 1 2 3 45

Воспользуйтесь поиском по сайту: