 |
Опыт работы учителей по формированию понятия числа у младших школьников
|
|
|
|
Подходить творчески к разработке урока дело нелегкое, особенно, если учебник составлен поурочно, т.е. в нем предложено определенное количество заданий, которое нужно выполнить на данном уроке. Сложно это и тогда, когда планируешь изучение нового материала. На таком уроке хочется, чтобы изучение нового было рассмотрено с различных сторон.
Такой подход предлагается в учебнике «Математика-1» Н.Б.Истоминой и И.Б.Нефедовой. В нем для каждого урока дается 2-3 задания, а в методических рекомендациях предлагается внимательно просмотреть все предшествующие задания и ориентируясь на них, составить к новому уроку дополнительные. Такой подход создает благоприятные условия для творческой деятельности учителя, хотя, конечно, не все получается сразу. Здесь огромную помощь учителю оказывают сами задания, предложенные в учебнике, они помогают ему построить урок так, чтобы вся деятельность детей была подчинена основной цели урока.
Покажу это на примере урока, на котором дети знакомятся с числом и цифрой нуль.
Вот так выглядит страница учебника «Математика-1» Н.Б.Истоминой и И.Б.Нефедовой, связанная с изучением темы «Число и цифра 0».
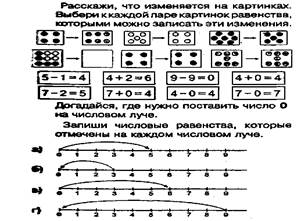
Все задания, предложенные на этой страницы, связаны с изучением нового вопроса. В то же время при выполнении этих заданий можно использовать материал, раннее изученный детьми. Кроме того, эти задания активизируют деятельность учащихся, так как они требуют от них анализа предложенных иллюстраций: сравнения, выбора равенств, соответствующих данным иллюстрациям, обоснования выполняемых действий, самостоятельной записи числовых равенств.
Ориентируясь на эту страницу, можно составить различные варианты уроков, а я хочу предложить свой вариант.
|
|
|
Сначала мы попросили учеников назвать числа, которые им известны. Предлагая такое задание, я не исключала возможности, что дети назовут и числа больше 10. Но, видимо, потому, что на уроках эти числа еще не рассматривались, ученики назвали только числа от 1 до 9. Поэтому свою беседу построила так:
- Сегодня мы познакомимся еще с одним числом и цифрой (знаком), которой это число записывается (обозначается). Как вы думаете, какое это число? (10,0).
Посмотрите, кто из вас прав? (Зажигаю на электротабло 8 огоньков.)
Какой цифрой обозначим число огоньков? (Ученики выставляют на фланелеграфе карточку с цифрой 8).
Гашу на табло 2 огонька.
Что изменилось на табло? (Огоньков стало на 2 меньше, огоньков стало 6.)
Поставим на фланелеграф цифру, которой обозначается это число.
Гашу еще 2 огонька, затем еще 2. Дети выставляют цифры 4 и 2. На фланелеграфе ряд чисел: 8, 6, 4, 2. Гашу последние 2 огонька.
А теперь, что вы видите на табло? (Нет ни одного огонька, нет ничего, табло пустое.)
А может кто-нибудь знает, каким знаком в математике можно обозначить то, что на табло нет ни одного огонька? Дети выставляют на фланелеграфе карточку с цифрой 0.
Верно, этим знаком записывается число нуль.
Цифра вроде буквы «О» —
Это ноль иль ничего.
Этот ноль такой хорошенький,
Но не значит ничегошеньки.
Такой цифрой (знаком) 0 впервые стали обозначать в Индии, а его название возникло от латинского слова nullum, что в переводе на русский обозначает ни одного, нисколько.
А кто может сказать, по какому правилу записан на доске ряд чисел: 8, 6, 4, 2, 0? (Числа уменьшаются; числа уменьшаются на 2.)
-Давайте поучимся красиво писать цифру 0.
На доске даю образец записи, объясняю, как писать эту цифру. Вызываю к доске детей, и они сами пробуют написать цифру 0. Каждый раз обсуждаем, что получилось хорошо, а что не удается, кто написал цифру 0 правильно. Дети пишут цифру «в воздухе», потом в тетрадях.
|
|
|
-Итак, мы научились писать цифру 0. А теперь хотите познакомиться с тайнами этого числа? (Да, да.)
Послушайте стихотворение:
Повезло опять Егорке:
У реки сидит не зря —
Два карасика в ведерке
И четыре пескаря.
Но смотрите, у ведерка
Появился хитрый кот.
Сколько рыб теперь Егорка
На уху нам принесет?
-Кто хочет на фланелеграфе изобразить картинку к этому стихотворению?
На фланелеграфе прикрепляется ведерко, в него помещается сначала 2 карася, затем 4 пескаря.
- Запишите в тетради равенство, которое соответствует этому действию. Дети записывают самостоятельно: 2+4=6.
- Что случилось потом? Кто будет хитрым котом? Выходи и покажи, как изменится наша картинка.
Ученик выходит к доске и снимает 6 рыбок.
- А каким равенством надо записать это действие?
Дети самостоятельно записывают в тетрадях: 6—6=0. Пока они пишут, я возвращаю рыбок на фланелеграф (в ведерко).
- Посмотрите, в ведре опять 6 рыбок. Закройте глаза, я что-то изменю на картинке. Убираю 1 рыбку. Каким равенством запишем то, что я сделала? (6—1=5.)
Повторяю задание, убираю еще одну рыбку. В тетрадях дети записывают: 5—1=4.
Опять предлагаю закрыть глаза и ничего не меняю на картинке.
- Откройте глаза. Что изменилось? (Ничего.)
- Догадайтесь, как можно это записать равенством?
Дети предлагают: 4—0=4, 4+0=4.
- Что показывает эта запись? (Ни одной рыбки не убрали, ни одной рыбки не добавили.)
- Откройте учебник.
Ученик читает задание и объясняет, что на первой картинке слева 4 круга, а справа 6, кругов стало больше на 2, значит, этой паре картинок подходит равенство 4+2=6.
Аналогично обсуждаются все пары картинок. Интересно, что и картинке (вторая во втором ряду), на которой изображено по четыре кружка, подходят два равенства: 4+0=4 и 4—0=4.
Естественно, дети пытаются найти и к следующей картинке тоже два равенства, но дано только одно 7—0=7. Тогда они сами предлагают другое 7+0=7. Некоторые говорят, что одно равенство записано неверно (7+0=4), и, если вместо 4 написать 7, то это равенство подойдет к последней паре картинок.
Меня радует, что дети дают такие ответы. Это показатель того, что они анализируют рисунки и осмысленно соотносят с ними числовые равенства.
|
|
|
- А если рассматривать изменения в каждой паре картинок не слева направо, как это дано в учебнике, а справа налево, то какие равенства можно записать к каждой паре?
Предлагаю сделать это самостоятельно, кто сколько успеет за 5 минут.
После этого дети легко находят место нуля на числовом луче, и мы выясняем, что в этом случае обозначает число «0» (не отложили ни одной мерки, начало луча).
Определив место нуля на числовом луче, мы выполняем задание № 106. Дети самостоятельно записывают в тетрадях равенства: 0+5=5, 3—3=0, 0+6=6, 9—9=0.
При проверке они читают равенства используя (кто может) математические термины (слагаемое, значение суммы) и поясни ют, что обозначает каждое число в равенстве на числовом луче.
Затем они на числовых лучах находят значения выражений:
0+3+2 /луч а/
0+4+2 /луч в/
9—7—2 /луч г/
Дети накладывают на страницу учебник прозрачную пленку и выполняют задание. Выясняем, какие изменения они внесли на каждом лучевом числе.
Наконец, предлагаем последнее задание. Его нет в учебнике, но мне хочется проверить, догадаются ли наши ученики, как изобразить на числовом луче такие равенства: 3—0=3, 5+0=5.

Задание выполняется самостоятельно, в индивидуальных карточках. Справляются все.
Подводим итог:
- С какими тайнами нуля мы познакомились сегодня на уроке? (К числу прибавляем нуль, получаем это число; из числа вы читаем нуль, получаем это же число; если и трех вычесть 3, то получим нуль; если и любого числа вычесть это же число, получи нуль).
-А если к нулю прибавить нуль? А ее ли из нуля вычесть нуль?
Так кто же был прав, с каким числом и с какой цифрой мы познакомились сегодня на уроке?
Урок принес большое удовлетворение детям, а это очень важно для дальнейшего поиска и творчества.
|
|
|


