Выполнения отдельных этапов задания 1. 1
1.1.1. Основные определения. Электрическая цепь - это совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, электрическом токе и электрическом напряжении.
Электрический ток - это явление направленного движения свободных носителей электрического заряда q в веществе или в пустоте, количественно характеризуемое скалярной величиной, равной производной по времени от электрического заряда, переносимого свободными носителями заряда сквозь рассматриваемую поверхность, т.е.
 (1.1)
(1.1)
Из выражения (1.1) получают единицу тока
[ I ] = [ q ]/[ t ] = Кл/c = A × c /c = A (ампер).
Постоянный электрический ток (в дальнейшем ток) – это неизменное и однонаправленное движение заряженных частиц (зарядов). При постоянном токе в течение каждого одинакового промежутка времени D t переносится одинаковый заряд D q. Поэтому ток I = q / t, где q - весь заряд (Кл) за время t (с).
Условное положительное направление тока I во внешней (от источника энергии) цепи противоположно направлению движения потока электронов (электрон – частица, обладающая наименьшим отрицательным зарядом (qe = -1,602×10-19 Кл, тогда 1 Кл = 6,24×1018 электронов), т. е. он протекает от точки а с большим потенциалом к точке b с меньшим потенциалом, вызывая падение напряжения (в дальнейшем напряжение) на сопротивлении этого участка
Uab = j а – j b. (1.2)
Э лектрическое напряжение – это работа, затрачиваемая на перенос единицы заряда (1 Кл) из точки а в точку b электрическогополя по произвольному пути. Однозначно определяют только разность потенциалов (напряжение) между соответствующими точками. Когда говорят о потенциале точки электрической цепи, то подразумевают разность потенциалов между этой точкой и другой (обычно заземлённой), потенциал которой принимают равным нулю.
Электродвижущая сила E (в дальнейшем ЭДС E в вольтах) источника энергии численно равна работе (энергии) W в джоулях (Дж), затрачиваемой сторонним и индуктированным электрическими полями на перемещение единицы заряда (1 Кл) из одной точки поля в другую.
1.1.2. Состав электрической цепи. Любая электрическая цепь состоит из следующих элементов:
· источников энергии (активныхэлементов), преобразующих различные виды энергии в электрическую. Это генераторы электрических станций, аккумуляторные и солнечные батареи, термопары и др.;
· приёмников электрической энергии (пассивныхэлементов), в которых электрическая энергия преобразуется в другие виды: тепловую (нагревательные элементы), механическую (электрические двигатели), световую (люминесцентные лампы), химическую (гальванические ванны) и др.;
· вспомогательных элементов (проводов, выключателей, предохранителей, резистивных регуляторов тока, измерительных приборов, разъёмов и др.).
Электрические цепи принято изображать в виде электрических схем: принципиальных, монтажных, схем замещения и др.
Схема электрической цепи – это её графическое изображение, содержащее условные обозначения элементов цепи и показывающее соединения этих элементов.
При анализе электрических цепей их заменяют схемами замещения. Схема замещения электрической цепи – это её расчётно-математическая модель, содержащая идеальные пассивные (резистивные, индуктивные и ёмкостные) и активные (источники напряжения и источники тока) элементы. Элементом электрической цепи называют отдельное устройство, выполняющее в цепи определённую функцию Эти элементы являются эквивалентами (моделями) реальных устройств цепи, которым теоретически приписывают определённые электрические и магнитные свойства, отражающие главные (доминирующие) процессы в элементах цепи.
Пассивными называют элементы электрической цепи, которые не способны генерировать электрическую энергию. К пассивным элементам относят резисторы, индуктивные катушки и конденсаторы (табл. 1.1.1).
Резистор – это пассивный элемент электрической цепи, предназначенный для использования его электрического сопротивления R. Резистор не может накапливать энергию: полученная им электрическая энергия необратимопреобразовывается в нёмв тепловую энергию.
Т а б л и ц а 1.1.1. Пассивные элементы цепей и их характеристики
Индуктивная катушка – это пассивный элемент цепи, предназначенный для использования его собственной индуктивности L и/или его магнитного поля. При нарастании тока в индуктивной катушке происходит преобразование электрической энергии в магнитную и её накопление в магнитном поле катушки, а при убывании тока – обратное преобразование энергии магнитного поля в электрическую энергию, возвращаемую источнику.
Конденсатор – это пассивный элемент цепи, предназначенный для использования его электрической ёмкости С. При нарастании напряжения на зажимах конденсатора в нём происходит преобразование электрической энергии внешнего источника в энергию электрического поля за счёт накопления зарядов противоположных знаков на двух его электродах (пластинах). При уменьшении напряжения происходит обратное преобразование энергии электрического поля в электрическую энергию, возвращаемую источнику.
Активные элементы - это источники электрической энергии (аккумуляторы, генераторы и др.). Различают:источники напряжения (ИН) и источники тока (ИТ) в зависимости от их внутреннего сопротивления (табл. 1.1.2). В источнике напряжения внутреннее сопротивление R вт значительно меньше сопротивления R нагрузки (в идеальном ИН R вт = 0), а в источнике тока R вт значительно больше сопротивления R нагрузки (в идеальном ИТ R вт = ¥), а проводимость (в сименсах)
G вт = 1/ R вт << G = 1/ R.
Т а б л и ц а 1.1.2. Активные элементы цепей и их характеристики
| Активный элемент
| Схема источника энергии и его график внешней характеристики (ВАХ) U = f (I)
| Уравнение
ВАХ
|
|
Источник напряжения (ИН)
|
|
 В, В,

|
|
Источник тока (ИТ)
|
|
 ,
J – ток ИТ,
G вт = 1/ R вт ,
J – ток ИТ,
G вт = 1/ R вт
|
| П р и м е ч а н и е: 1 – ВАХ идеализированных источников энергии; 2 – ВАХ реальных источников; 3 – ВАХ идеальных источников энергии
|
1.1.3. Топологические параметры схем цепей. При анализе электрических схем пользуются следующими топологическими параметрами схем:
· ветвь (В) - участок электрической цепи, вдоль которого протекает один и тот же электрический ток;
· узел (У) - место соединения ветвей электрической цепи. Обычно место, где соединены две ветви, называют не узлом, а соединением (или устранимым узлом), а узел соединяет не менее трёх ветвей;
· контур - последовательность ветвей электрической цепи, образующая замкнутый путь, в которой один из узлов одновременно является началом и концом пути, а остальные встречаются только один раз. В электрической цепи выделяют линейно независимые контуры k н, которые отличаются друг от друга хотя бы одной ветвью. Число независимых контуров зависит от числа ветвей В и числа узлов У в цепи:
k н = В – (У – 1). (1.3)
Так, в схеме электрической цепи (рис. 11.1) ветвей В = 5, узлов У = 3, соединений 2, независимых контуров k н = 3.
П р и м е ч а н и я.
1. Точки 5, 6, 7 и 8 имеют одинаковый электрический потенциал, поэтому они могут быть геометрически объединены в одну общую точку - узел.
2. Точки 1 и 4 соединяют по два элемента, поэтому их называют точками соединений двух элементов, а не узлами.
| Рис. 1.1.1. Схема электрической цепи
|
1.1.4. Задача расчёта цепи. Расчёт электрической цепи заключается в описании её схемы замещения математическими уравнениями и в решении системы уравнений относительно электрических величин. Теория электрических и магнитных цепей базируется на введении параметров отдельных участков цепи, из которых основными являются сопротивления, индуктивности и ёмкости. Помимо этих параметров, вводят в рассмотрение еще множество других (например, магнитное сопротивление магнитной цепи, реактивные сопротивления и проводимости цепи переменного тока, и др.), находящихся в известной связи с ними или имеющих самостоятельное значение.
Задачей расчёта электрической цепи является, в первую очередь, определение токов и напряжений ветвей при заданных значениях параметров активных и пассивных элементов схемы цепи.
Для расчёта электрических цепей (точнее, их схем замещения) разработано несколько методов, наиболее общими из которых являются метод непосредственного применения законов Кирхгофа, метод узловых напряжений, метод переменных состояния, метод контурных токов.
П р и м е ч а н и е. Понятия «электрическая цепь» и «схема электрической цепи» часто отождествляют.
1.1.5. Законы Ома и Кирхгофа. Решение задач анализа электромагнитных процессов в известной схеме электрической цепи с заданными параметрами источников энергии и резистивных элементов базируется на применении закона Ома, первого и второго законов Кирхгофа, которые записывают соответственно для ветвей, узлов и контуров (табл. 1.1.3).
Закон Ома устанавливает зависимость между током и напряжением на пассивной ветви при совпадении направлений тока и напряжения на ней. (см. табл. П1.3, вторая строка). Для ветви с источниками напряжения используют обобщенный закон Ома: (см. табл. П1.3, третья строка). Знак плюс перед ЭДС E и напряжением U 12 записывают при совпадении их направлений с условно положительным направлением тока I и знак минус - при не совпадении их направлений с направлением тока.
Первый закон Кирхгофа (1ЗК) записывают для узлов электрической схемы (см. табл. П1.3, четвертая строка). Закон формулируется следующим образом: алгебраическаясумма токов в любом узле схемы цепи равна нулю. При этом токи, направленные к узлу, принято записывать со знаком плюс, а уходящие от узла, со знаком минус.
Второй закон Кирхгофа (2ЗК) применяется к контурам электрической цепи (см. табл. П1.3, пятая строка) и формулируется следующим образом: в любом контуре схемы алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех участках с сопротивлениями, входящими в этот контур. При этом ЭДС и напряжения на элементах контура записывают со знаком плюс, если выбранное направление обхода контура (например, по ходу часовой стрелки) совпадает с направлением напряжений (токов) на этих элементах, и со знаком минус при несовпадении.
Таблица 1.1.3. Топологические параметры схем цепей и их описание
| Топологический параметр
схемы
|
Участок схемы
| Основание для составления уравнения
| Выражение закона
|
|
Пассивная ветвь
|
|
Закон Ома
| 
|
|
Ветвь с источниками напряжения
|
|
Обобщенный закон Ома
| 
|
|
Узел
|
| Первый закон Кирхгофа (1ЗК)
|
å Ik = 0,
I 1 - J - I 2 - I 3 = 0
|
|
Контур
|
|
Второй закон Кирхгофа (2ЗК)
|
å E k = å U k,
E 2 - E 3= R 1 I 1 +
+ R 2 I 2- R 3 I 3 - U 12
|
1.6. Метод расчёта, основанный на законах Кирхгофа. Анализ и расчёт любой электрической цепи постоянного тока можно провести в результате совместного решения системы уравнений, составленных посредством первого и второго законов Кирхгофа. Число уравнений в системе равно числу ветвей в цепи (N МЗК = В), при этомчисло независимых уравнений, которые можно записать по 1ЗК, на одно уравнение меньше числа узлов, т. е.
N 1ЗК = У - 1, (1.4)
а число независимых уравнений, записываемых по 2ЗК,
N 2ЗК = B - (У - 1), (1.5)
где В - число ветвей с неизвестными токами (без ветвей с источниками тока); У - число узлов.
Составим посредством законов Кирхгофа необходимое число уравнений для определения токов ветвей схемы (рис. 1.1.2), если заданы ЭДС E 1 и E 2 источников напряжения, ток J источника тока и сопротивления R 1,…, R 5 резисторов.
N МЗК = N 1ЗК + N 2ЗК = В.
С этой целью:
1. Проведём топологический анализ схемы для определения числа независимых уравнений. В схеме B 1 = 6 ветвей, У = 3 узла. Однако в ветви с ИТ ток J задан, поэтому число независимых ветвей В = 5. Число независимых уравнений для решения задачи по методу законов Кирхгофа
N МЗК = В = 5.

2. Пронумеруем узлы и выберем произвольно направления токов в ветвях (рис. 1.1.3).

3. Составим уравнения по 1ЗК (
N 1ЗК =
У - 1 = 3 - 1 = 2):
для узла 1: I 1 - I 2 - J - I 3 = 0, (1)
для узла 2: I 3 - I 4 + I 5 = 0. (2)
4. Выберем независимые контуры и направление обхода контуров, например, по ходу часовой стрелки. В нашем случае имеется три независимых контура, так как ветвь с заданным током J ИТ в уравнениях, составляемых по2ЗК, не учитывается:
N 2ЗК = B - (У - 1) = 5 – (3 – 1) = 3.
5. Составим три уравнения по 2ЗК:
для контура 1'-1-0-1': E 1 = R 1 I 1 + R 2 I 2, (3)
для контура 1-2-0-1: 0 = R 3 I 3 + R 4 I 4 - R 2 I 2, (4)
для контура 2-2'-0-2: - E 2 = - R 5 I 5 - R 4 I 4 . (5)
6. Решив систему уравнений (1)…(5), например, методом Гаусса или с использованием формул Крамера можно определить все неизвестные токи ветвей цепи.
1.1.7. Структурные преобразования схем замещения цепей. Расчёт электрических цепей можно упростить путём преобразованияих схем замещения в более простые и удобные для расчёта. Такие преобразования приводят, как правило, к уменьшению числа узлов схемы и, следовательно, необходимого числа исходных уравнений для расчёта.
Так, ветвь с последовательно соединёнными резисторами R 1, R 2, …, Rn может быть преобразована в простую схему с одним резистивным элементом (рис. 1.1.4 а), эквивалентное сопротивление которого равно сумме сопротивлений:
 (1.6)
(1.6)
а ветвь с несколькими последовательно соединёнными источниками напряжения и резисторами (рис. 1.1.4 б) также может быть преобразована в ветвь с одним эквивалентным ИН с параметрами R э и Е э (рис. 1.1.4 в):
 и
и  (1.7)
(1.7)
Параллельно соединённые резисторы с сопротивлениями
R 1,
R 2,…,
Rn (рис. 1.1.5
а) можно заменить одним резистором с проводимостью
G э (рис. 1.1.5
б).
Так как напряжение на всех ветвях одно и тоже, равное U, то токи ветвей

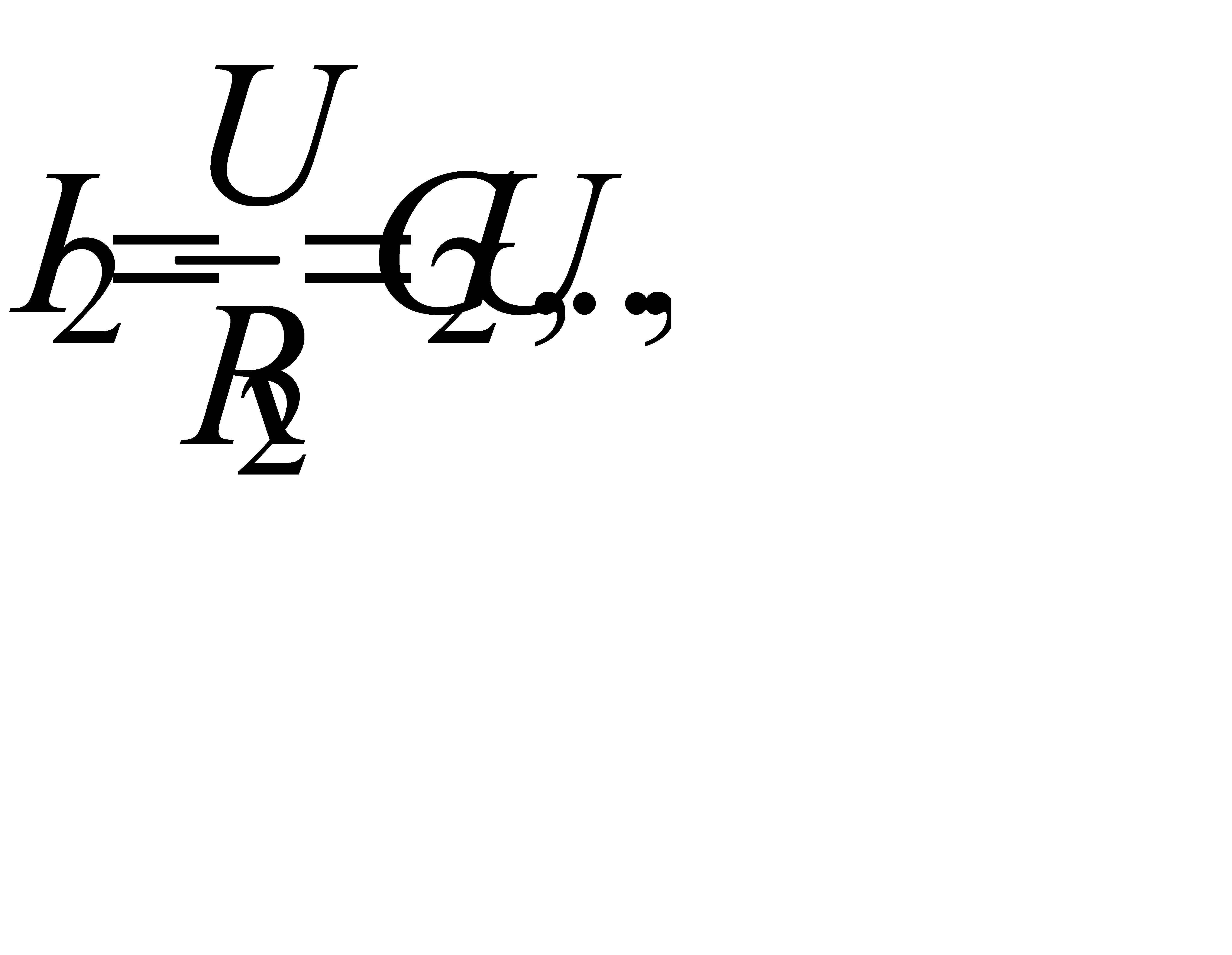

где  ,
, 
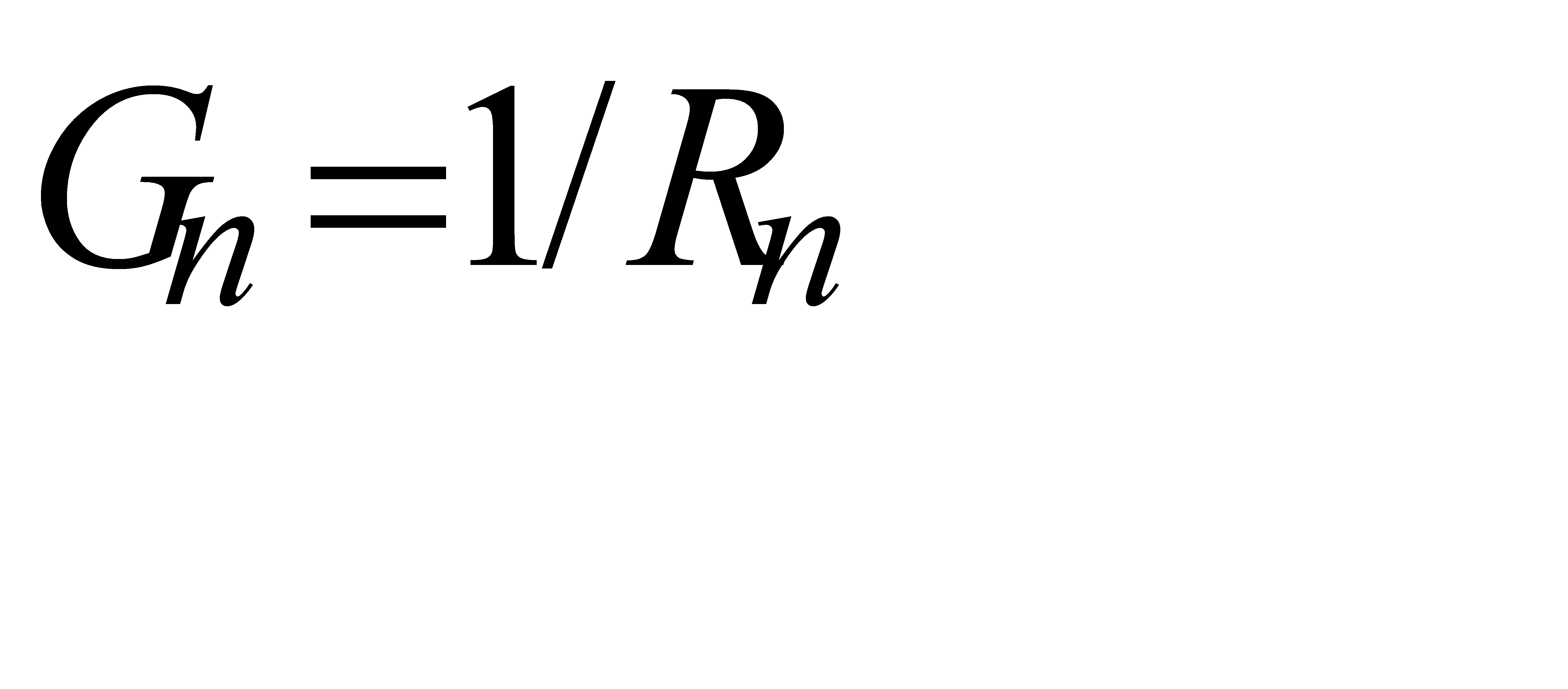 - проводимости ветвей в сименсах.
- проводимости ветвей в сименсах.
В схеме с двумя узлами 1 и 2 (см. рис. 1.1.5 а) ток на входе цепи

а эквивалентная проводимость и эквивалентное сопротивление пассивного участка цепи между узлами 1 и 2 равны
 и
и  . (1.8)
. (1.8)
Электрические схемы, имеющие сочетание последовательного и параллельного соединений участков цепи (смешанное соединение), могут быть преобразованы в более простые эквивалентные схемы путём замены параллельных ветвей одной ветвью, а последовательно соединённые участки цепи – одним участком. Так, например, для схемы рис. 1.1.6 а вначале нужно найти эквивалентное сопротивление параллельного участка 2 - 3 с тремя параллельно включенными резисторами
 , (1.9)
, (1.9)
а затем сложить его с сопротивлением
R 1 (рис. 1.1.6
б,
в):

В электрических цепях элементы могут быть соединены по схеме треугольник или по схеме звезда (рис. 1.1.7). Треугольником называют соединение трёх элементов, в котором конец первого элемента соединён с началом второго, конец второго с началом третьего, а конец третьего с началом первого (рис. 1.1.7 а). Звездой называют соединение, в котором концы трёх элементов соединены в одну общую точку п (рис.
1.1.7
б).
С целью уменьшения числа узлов в схеме цепи соединения элементов треугольником преобразуют в эквивалентное соединение звездой посредством следующих формул:

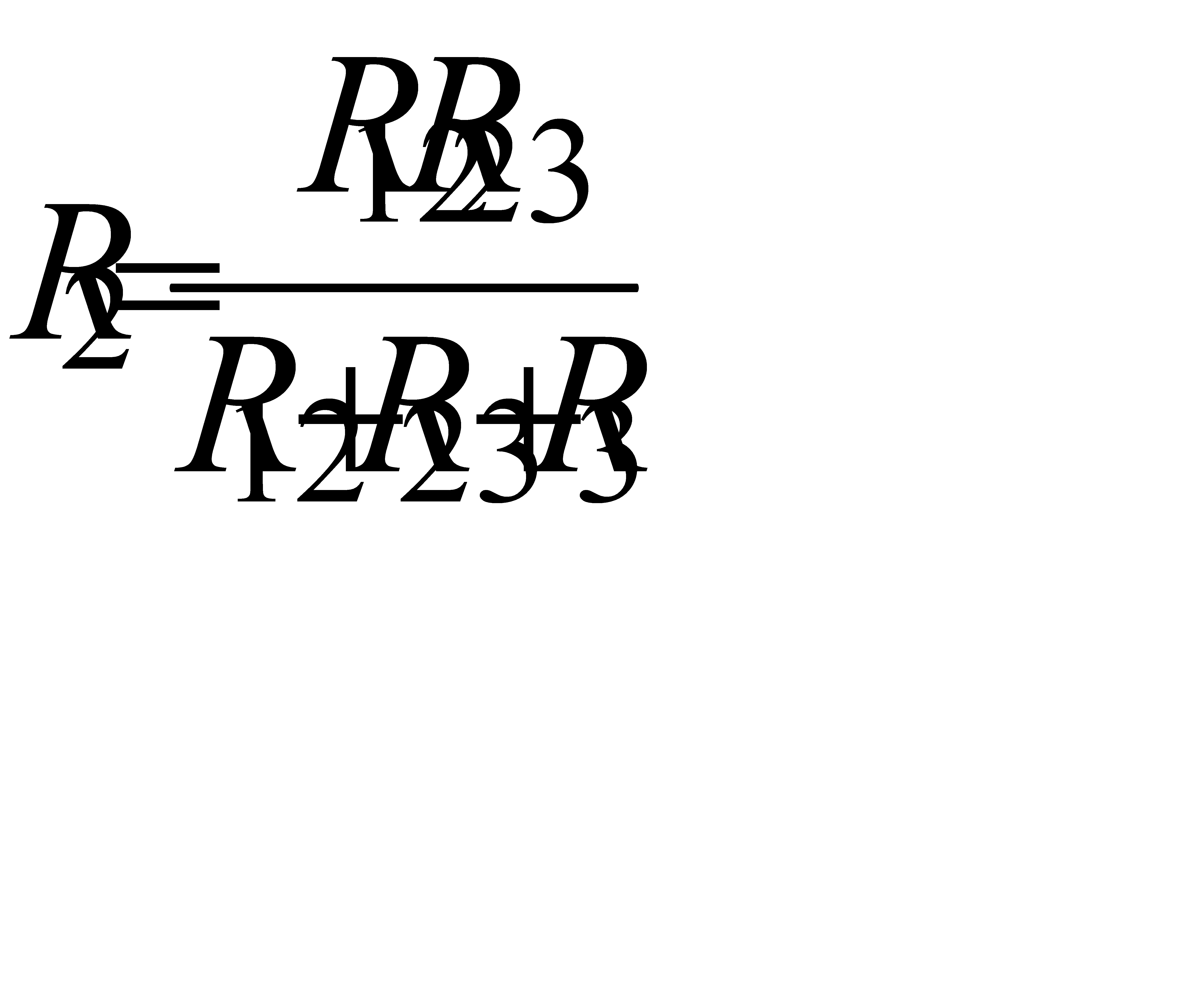 ,
,  , (1.10)
, (1.10)
т. е.сопротивление луча эквивалентной звезды равно дроби, в числителе которой произведение двух сопротивлений сторон треугольника, примыкающих к рассматриваемому узлу, делённому на сумму всех сопротивлений сторон треугольника.
1.1.8. Правило делителя напряжения. В ветви, состоящей их двух последовательно соединённых резисторов (рис. 1.1.8 а),напряжение на одном из резисторов равно приложенному к ветви напряжению, умноженному на сопротивление данного резистора и делённому на сумму сопротивлений обоих резисторов, т. е.

и
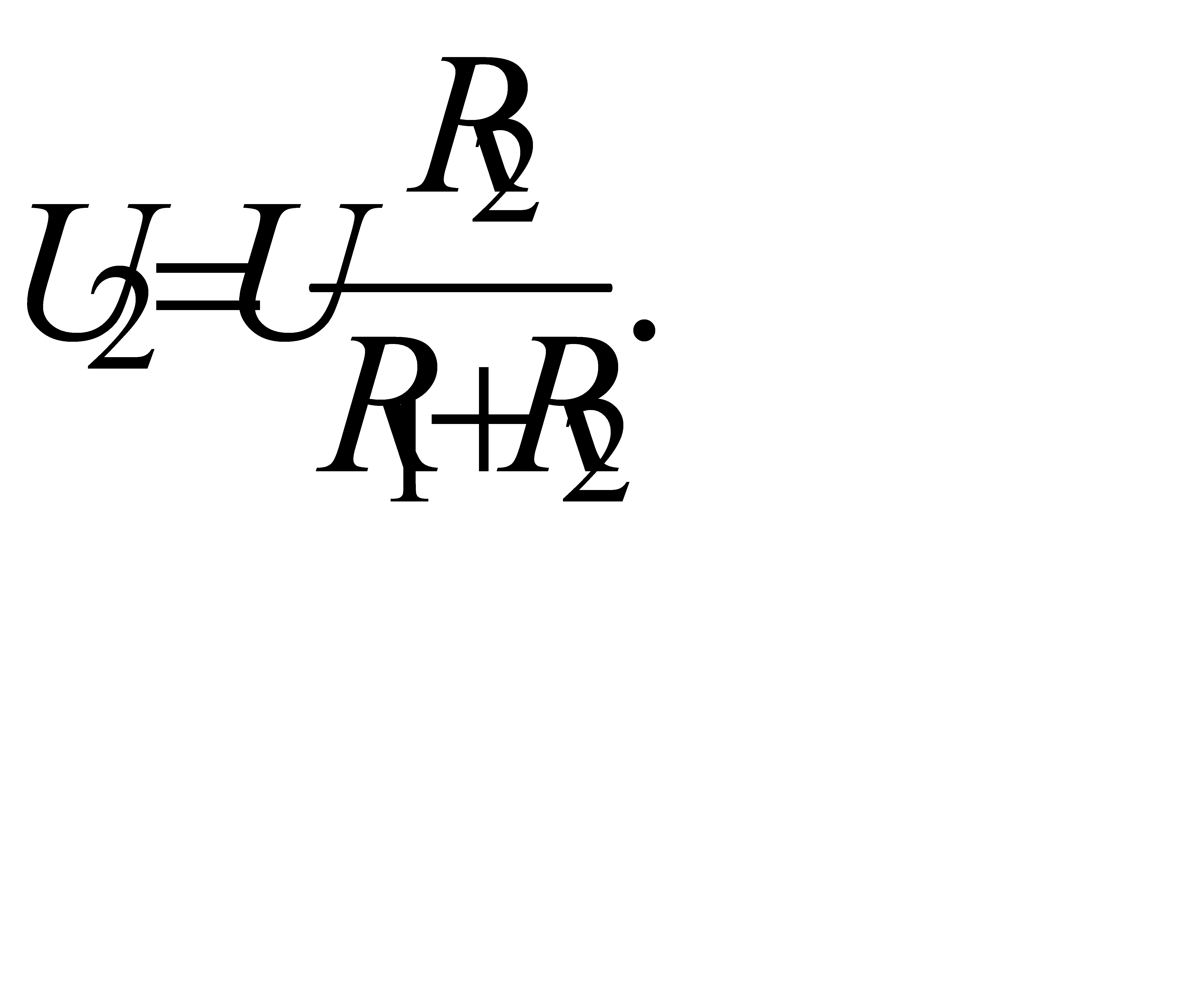
(1.11)
1.1.9. Правило делителя тока. Для цепи с двумя параллельно соединёнными резисторами (рис. 1.1.8 б) ток одной из двух параллельных ветвей цепи равен подходящему к разветвлению току I, умноженному на сопротивление другой (противоположной) ветви и делённому на сумму сопротивлений обеих ветвей, т.е.
 и
и  (1.12)
(1.12)
1.1.10. Метод узловых напряжений. Метод узловых напряжений (МУН) базируется на первом законе Кирхгофа и обобщенном законе Ома. В нём за вспомогательные расчётные величины принимают так называемые узловые напряжения U k 0 - напряжения между каждым k -м узлом схемы и выбранным базисным узлом (его будем обозначать цифрой 0), потенциал которого принимают равным нулю. Число уравнений для расчёта схемы по МУН
N МУН = У - 1. (1.13)
Для каждого узла, кроме базисного, составляют уравнение по 1ЗК. В полученных уравнениях токи ветвей, присоединённых к базисному узлу, выражают через узловые напряжения и проводимости посредством обобщённого закона Ома:
 (1.14)
(1.14)
где G k = 1/ R k - проводимость k -й ветви.
Токв ветви, подключённой к узлам k и j,
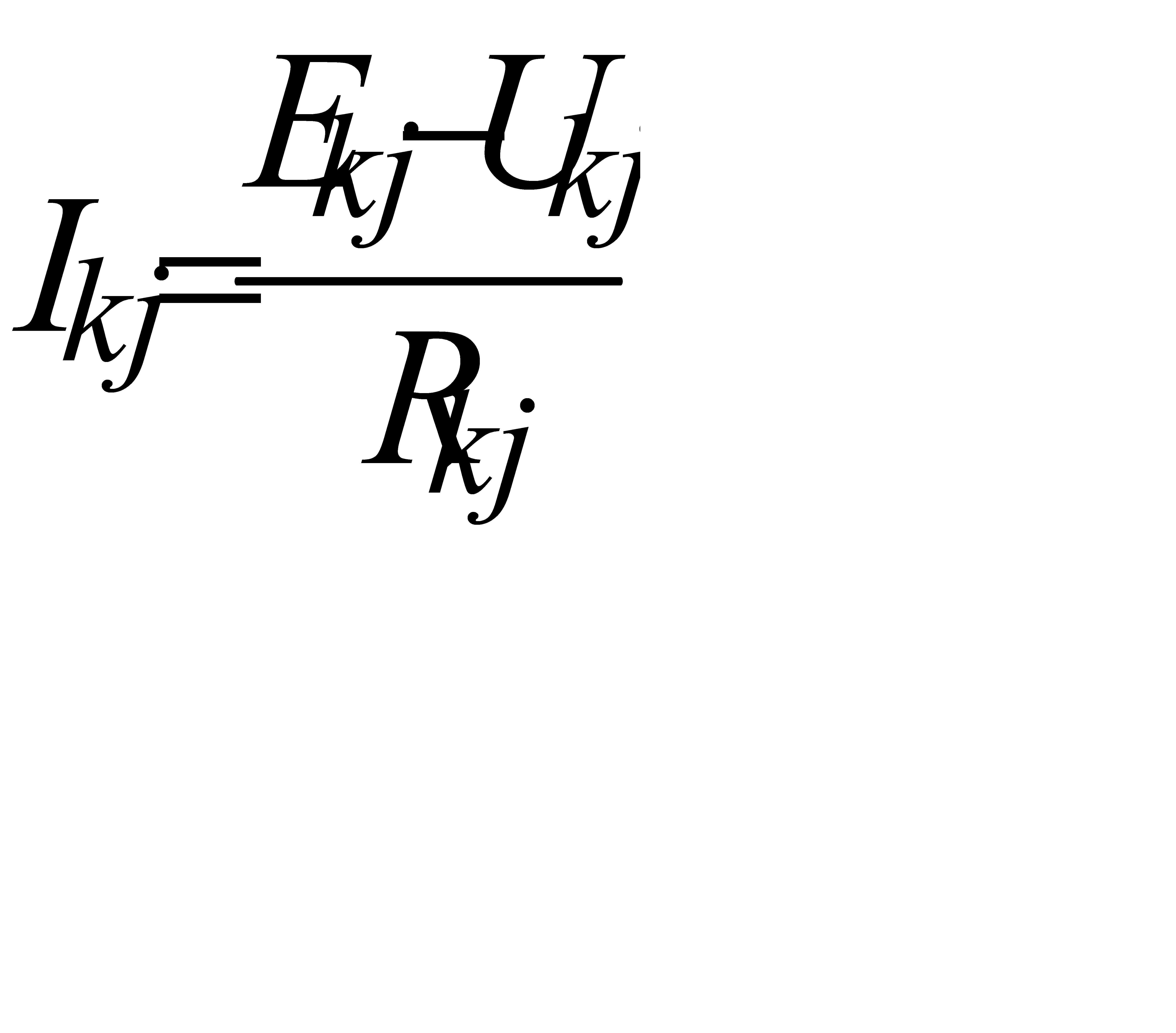 = (Ekj - U k 0 + U j 0) G kj, (1.15)
= (Ekj - U k 0 + U j 0) G kj, (1.15)
где U kj = U k 0 - U j 0 – межузловое напряжение; G kj = 1 /R kj - межузловая проводимость.
После группирования членов при соответствующих узловых напряжениях и переноса E k G k и токов J k источников тока в правую часть, получают систему уравнений относительно неизвестных узловых напряжений.
Структура каждого уравнения одинаковая, например, уравнение относительно узла 1:
G 11 U 10- G 12 U 20- ... - G 1 n Un 0 =  +
+  (1.16)
(1.16)
где G 11 = G 1 + G 2 +... + G n - собственная проводимость узла1, равная сумме проводимостей ветвей, присоединённых к узлу 1 (проводимости ветвей с ИТ не учитываются, так как G j = 1/ R j = 0 (R j = ¥)); G 12,..., G 1 n – межузловые проводимости;  +
+  - узловой ток узла 1;
- узловой ток узла 1;  - алгебраическая сумма произведений ЭДС ветвей, присоединённых к узлу 1, на проводимости этих ветвей, причём со знаком плюс (минус) записывают произведения, если ЭДС направлена к узлу 1 (от узла 1);
- алгебраическая сумма произведений ЭДС ветвей, присоединённых к узлу 1, на проводимости этих ветвей, причём со знаком плюс (минус) записывают произведения, если ЭДС направлена к узлу 1 (от узла 1);  - алгебраическая сумма токов источников тока ветвей, подключённых к узлу 1, причём токи Jk записывают со знаком плюс (минус), если они направлены к узлу 1 (от узла 1).
- алгебраическая сумма токов источников тока ветвей, подключённых к узлу 1, причём токи Jk записывают со знаком плюс (минус), если они направлены к узлу 1 (от узла 1).
Решив систему уравнений относительно узловых напряжений, определяют межузловые напряжения и токи ветвей посредством соотношений (1.14) и (1.15).
Пример 1.1.1. Пользуясь методом узловых напряжений, определить токи ветвей схемы (рис. 1.1.9), если E 1 = 12В, E 5 = 15В, J = 2А, R 1 = 1 Ом, R 2 = 5 Ом, R 3 = R 4 = 10Ом, R 5 = 1 Ом. В схеме 6 ветвей и 3 узла.
Решение. 1. Выбираем базисный узел 0 и направления узловых напряжений U 10 и U 20 от узлов 1 и 2 к базисному (см. рис. 1.1.9).

2. Составляем (N МУН = У - 1 = 3 - 1 = 2) уравнения по МУН:
для узла 1: G 11 U 10- G 12 U 20= E 1 G 1 - J,
для узла 2: - G 21 U 10 + G 22 U 20 = E 5 G 5,
где G 11 = G 1 + G 2 + G 3, G 12 = G 3 = 1/ R 3, G 22 = G 3 + G 4 + G 5, G 21 = G 12 = G 3.
3. После подстановки числовых значений (G 1 = 1/ R 1 = 1 См, G 2 = 0,2 См, G 3 = G 4= 0,1 См, G 5 = 1 См) имеем:
1,3 U 10 - 0,1 U 20 = 12 - 2 = 10,
- 0,1 U 10 + 1,2 U 20 = 15.
4. Воспользовавшись формулами Крамера, находим узловые напряжения:


Примечание. Вычисление узловых напряжений нужно проводить с большой точностью. В данном примере достаточно округлить четвёртый знак после запятой.
5. Межузловое напряжение
U 12 = U 10 - U 20 = 8,7097 - 13,226 = - 4,5163 B.
6. Искомые токи ветвей (см. выбранные направления токов ветвей на рис. П1.9):
I 1 = (E 1 - U 10) G 1 = 3,29 A, I 2 = U 10 G 2 = 1,754 A,
I 3 = U 12 G 3 = - 0,452 A, I 4 = U 20 G 4 = 1,323 A,
I 5 = (- E 5 + U 20) G 5 = -1,774 A.
7. Проверим результаты расчёта токов. Согласно 1ЗК для узла 2:
 = I 3 - I 4 - I 5 = - 0,452 - 1,323 + 1,774 = 0.
= I 3 - I 4 - I 5 = - 0,452 - 1,323 + 1,774 = 0.
1.1.11. Метод двух узлов. Метод двух узлов является частным случаем метода узловых напряжений и применяется для расчёта схем, содержащих (после преобразования) два узла и произвольное число параллельных пассивных и активных ветвей. Для расчёта токов ветвей цепи составляют и решают одно уравнение узлового напряжения  , равное алгебраической сумме токов, создаваемыхвсеми источниками напряжения и источниками тока цепи, делённой на собственную проводимость узла
, равное алгебраической сумме токов, создаваемыхвсеми источниками напряжения и источниками тока цепи, делённой на собственную проводимость узла  , т. е.
, т. е.
 (1.17)
(1.17)
а токи ветвей определяют по обобщённому закону Ома (см. (1.14)).
|
|
|

 (1.1)
(1.1) , Ом
, Ом
 , В
, В
 , Вт
, Вт

 или
iL =
или
iL = 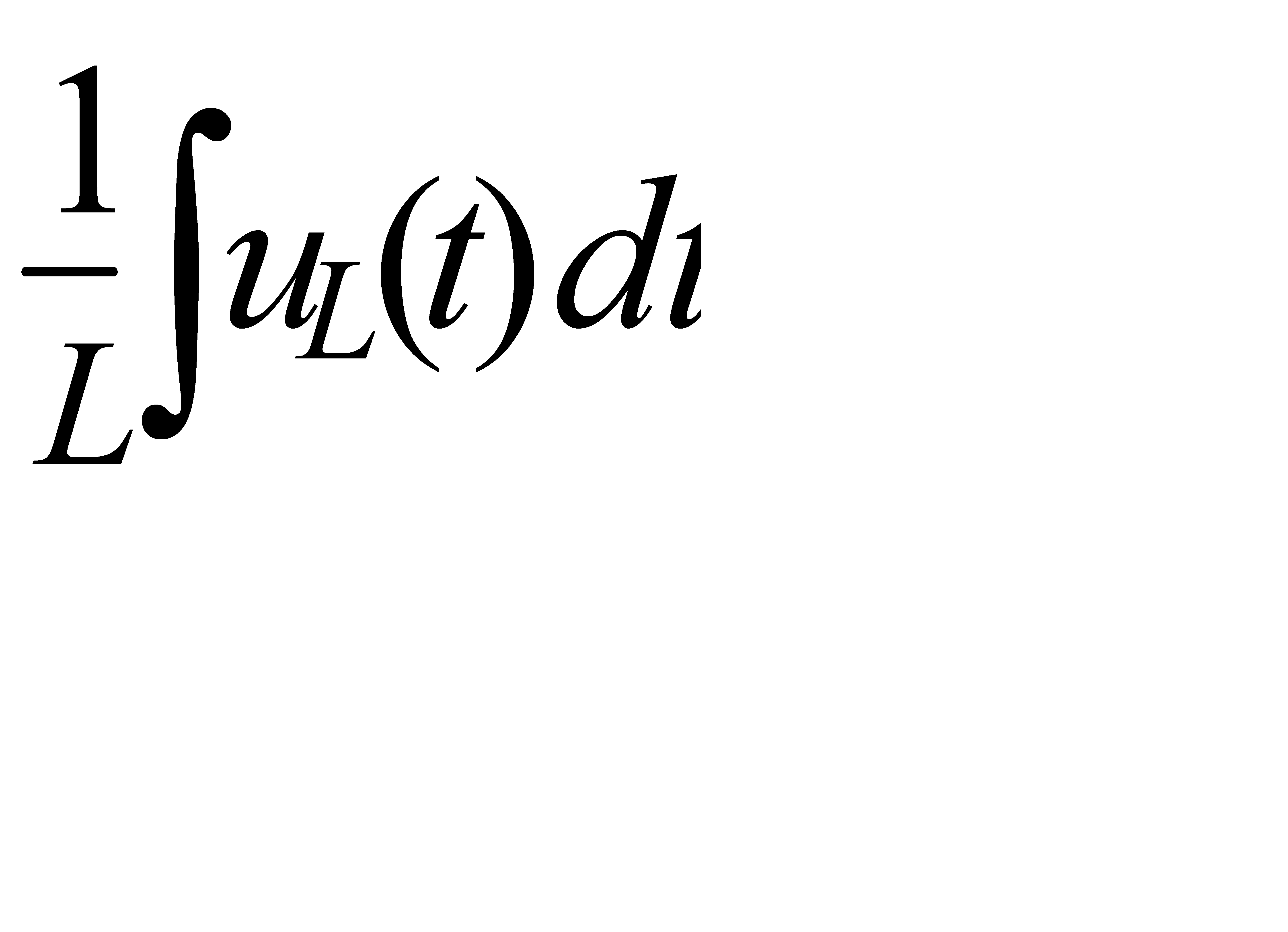
 или
или 
 В,
В,

 ,
J – ток ИТ,
G вт = 1/ R вт
,
J – ток ИТ,
G вт = 1/ R вт




 (1.6)
(1.6) и
и  (1.7)
(1.7)
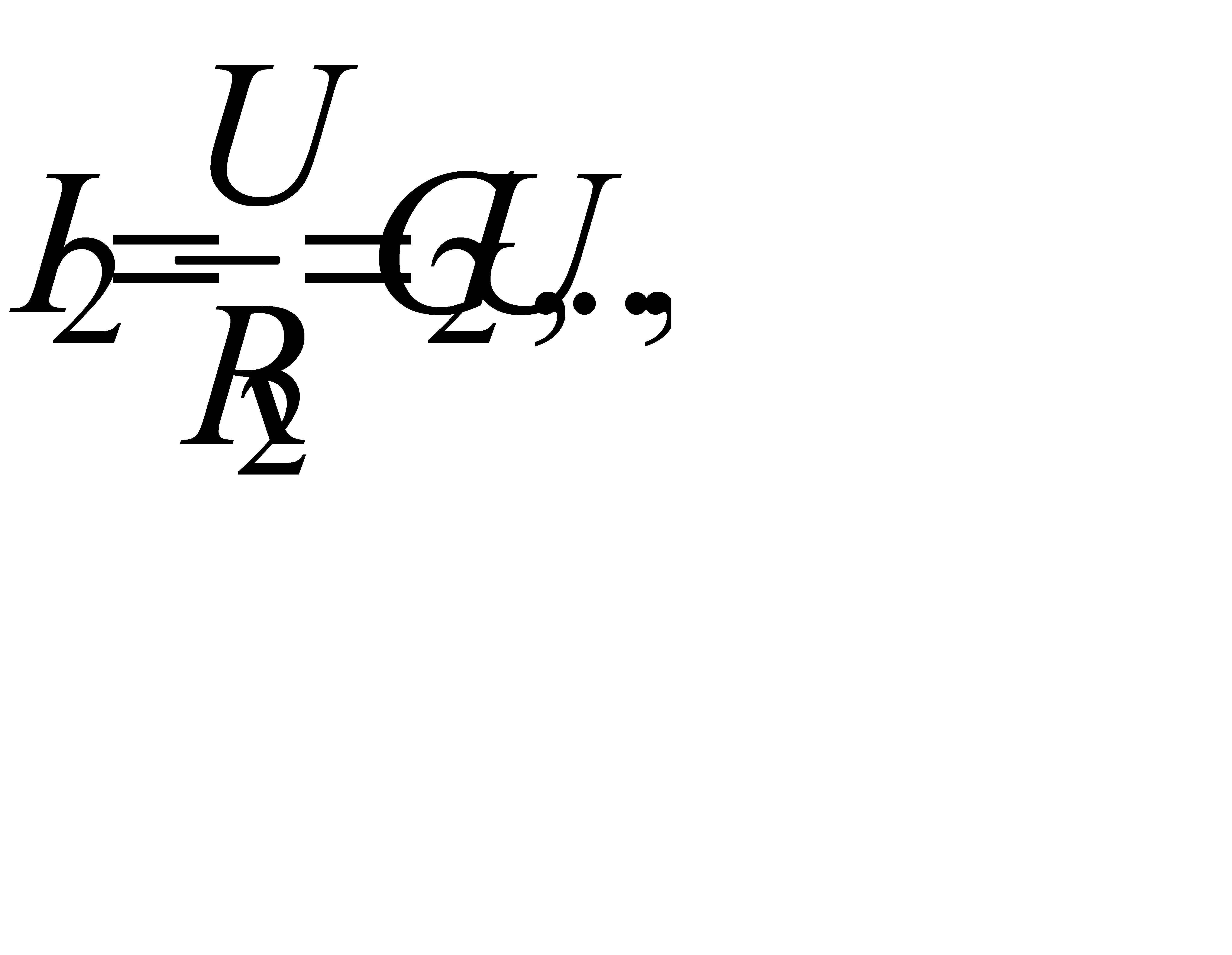

 ,
, 
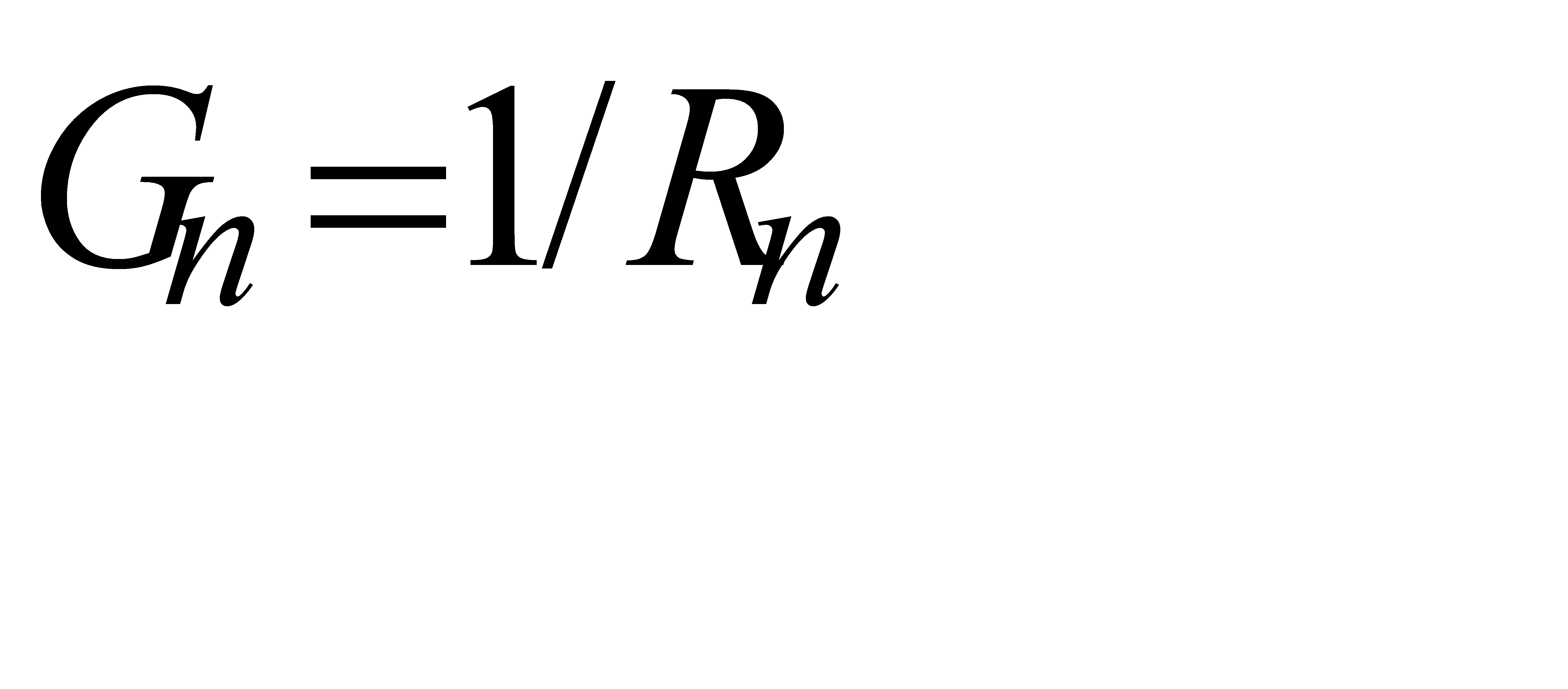 - проводимости ветвей в сименсах.
- проводимости ветвей в сименсах.
 и
и  . (1.8)
. (1.8) , (1.9)
, (1.9)

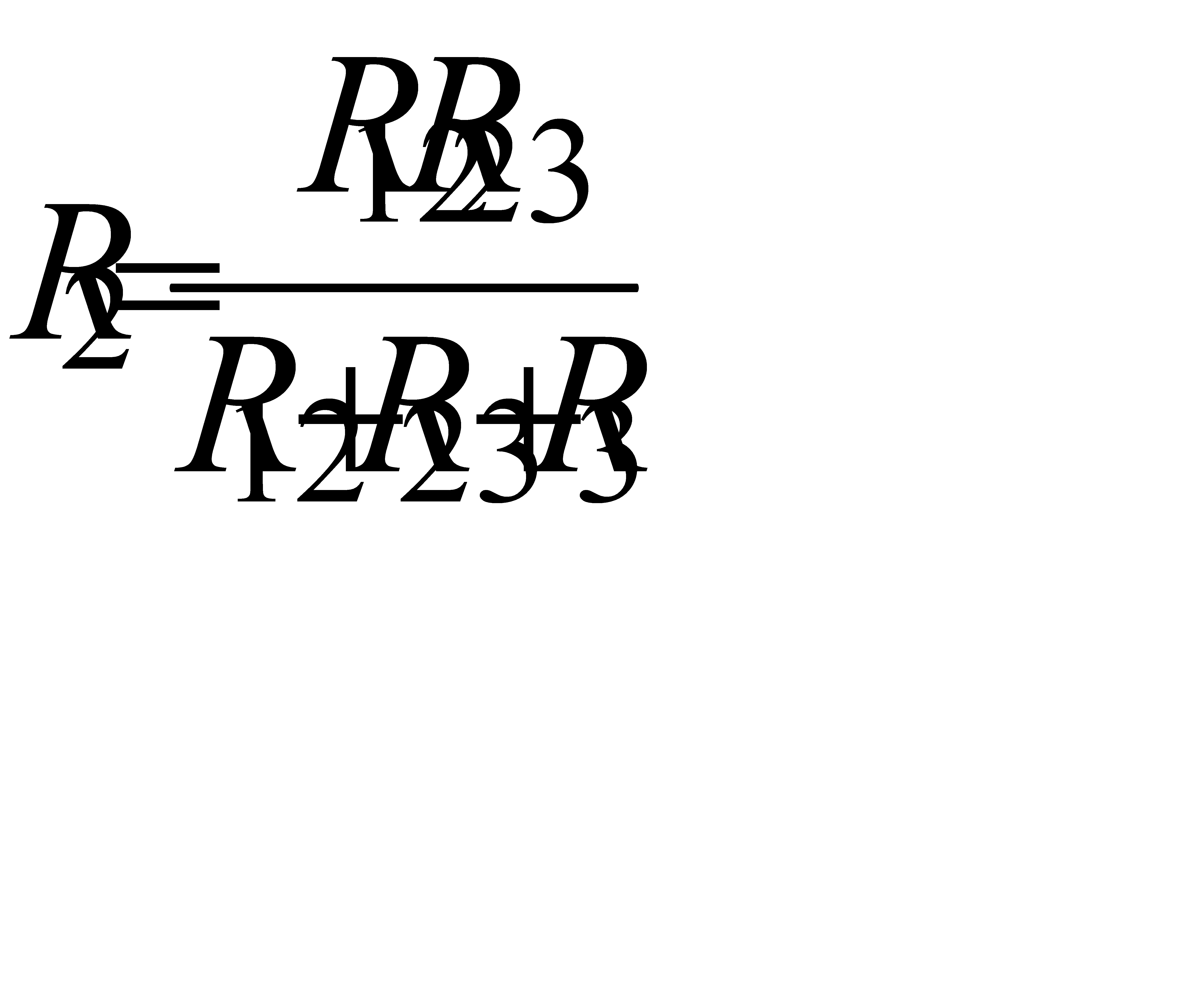 ,
,  , (1.10)
, (1.10) и
и 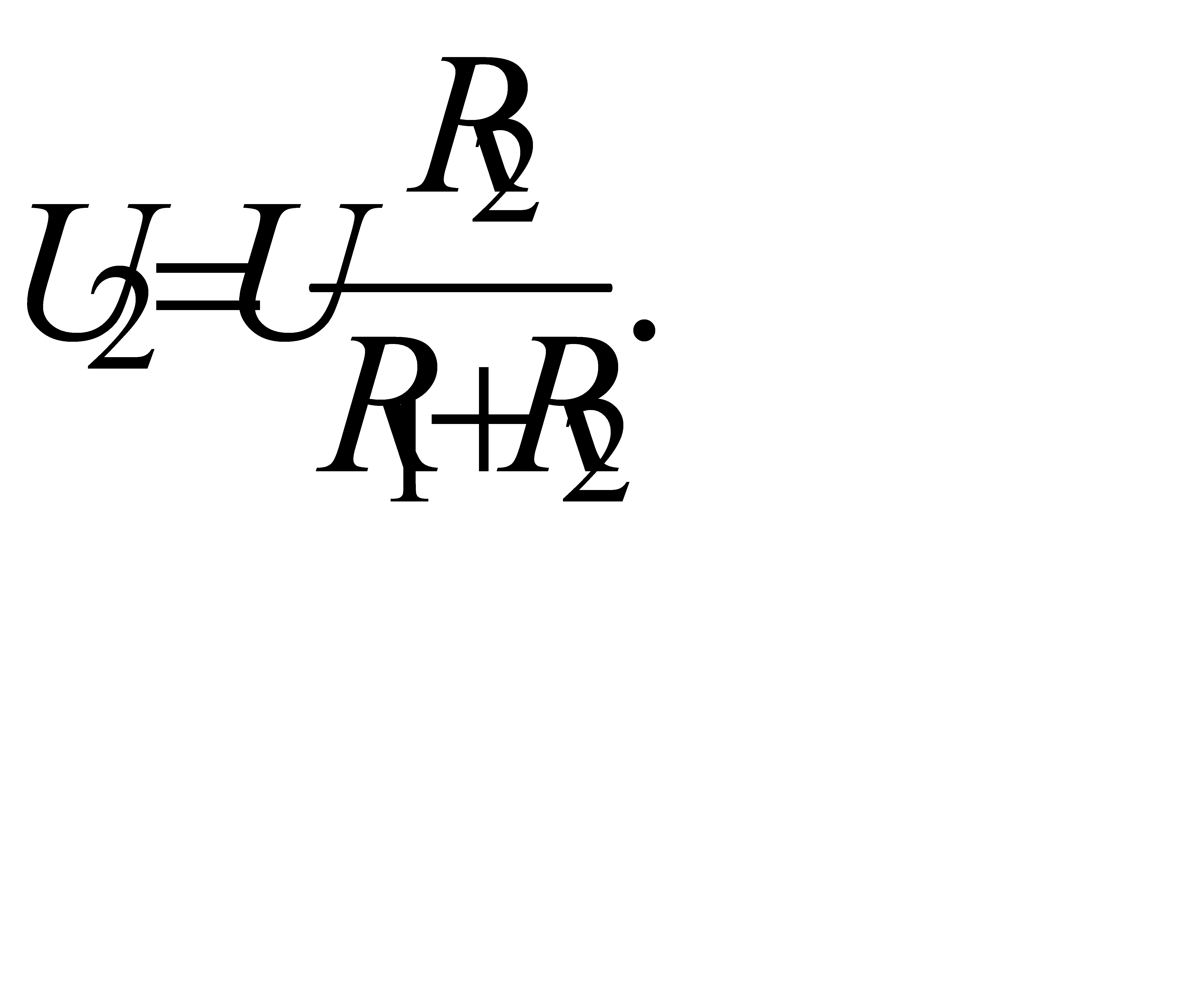 (1.11)
(1.11)
 и
и  (1.12)
(1.12) (1.14)
(1.14)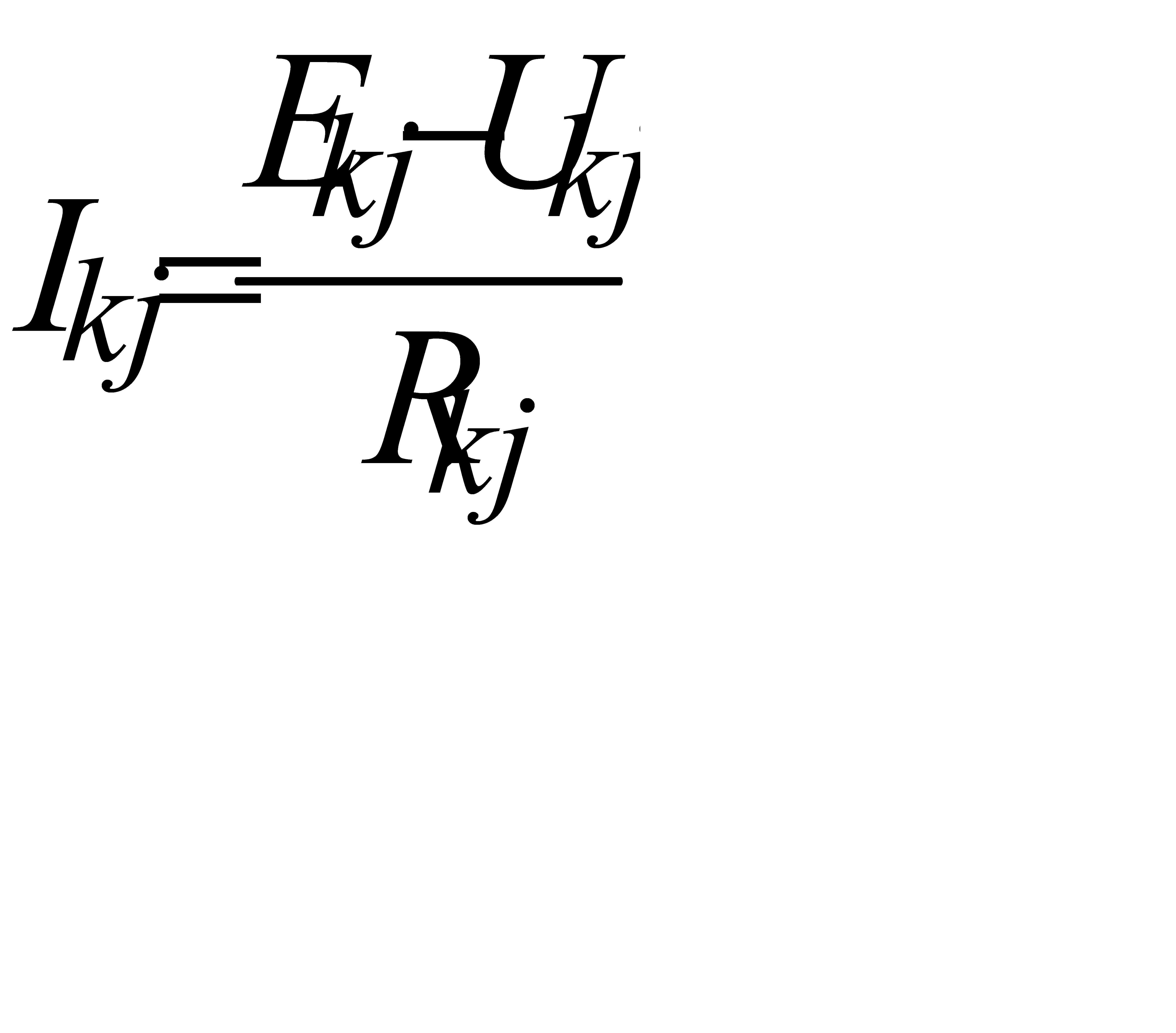 = (Ekj - U k 0 + U j 0) G kj, (1.15)
= (Ekj - U k 0 + U j 0) G kj, (1.15) +
+  (1.16)
(1.16) +
+  - узловой ток узла 1;
- узловой ток узла 1;  - алгебраическая сумма произведений ЭДС ветвей, присоединённых к узлу 1, на проводимости этих ветвей, причём со знаком плюс (минус) записывают произведения, если ЭДС направлена к узлу 1 (от узла 1);
- алгебраическая сумма произведений ЭДС ветвей, присоединённых к узлу 1, на проводимости этих ветвей, причём со знаком плюс (минус) записывают произведения, если ЭДС направлена к узлу 1 (от узла 1);  - алгебраическая сумма токов источников тока ветвей, подключённых к узлу 1, причём токи Jk записывают со знаком плюс (минус), если они направлены к узлу 1 (от узла 1).
- алгебраическая сумма токов источников тока ветвей, подключённых к узлу 1, причём токи Jk записывают со знаком плюс (минус), если они направлены к узлу 1 (от узла 1).


 = I 3 - I 4 - I 5 = - 0,452 - 1,323 + 1,774 = 0.
= I 3 - I 4 - I 5 = - 0,452 - 1,323 + 1,774 = 0. , равное алгебраической сумме токов, создаваемыхвсеми источниками напряжения и источниками тока цепи, делённой на собственную проводимость узла
, равное алгебраической сумме токов, создаваемыхвсеми источниками напряжения и источниками тока цепи, делённой на собственную проводимость узла  , т. е.
, т. е. (1.17)
(1.17)

