Основные теоретические положения и примеры
ВЫПОЛНЕНИЯ ОТДЕЛЬНЫХ ЭТАПОВ ЗАДАНИЯ 1.3
1.3.1. Основные определения. Трёхфазная цепь – это совокупность трёхфазной системы ЭДС, трёхфазной нагрузки (нагрузок) и соединительных проводов. Трёхфазной системой ЭДС (напряжений) называют систему, состоящую из трёх (однофазных) электрических цепей, в которых действуют три синусоидальные ЭДС одной и той же частоты, равные по амплитуде и сдвинутые по фазе относительно друг друга на угол 2p/3 (120°). Три ЭДС создаются в неподвижных обмотках, размещённых в пазах статора трёхфазного генератора под углом 120° относительно друг друга, при вращении ротора с намотанной на него катушкой, по которой протекает постоянный ток.
Под фазой трёхфазной цепи понимают участок цепи, по которому протекает одинаковый ток. Под фазой будем также понимать аргумент (w t - Y) синусоидальной функции. Таким образом, в зависимости от рассматриваемого вопроса, фаза - это либо участок трёхфазной цепи, либо аргумент синусоидальной функции.
| Рис. 1.3.1. Схемы соединения фаз трёхфазных генератора и приёмника
|
1.3.2. Схемы соединения фаз трехфазных генератора и приёмника. Обмотки статора трёхфазного генератора соединяют по схеме
звезда (Y) (рис. 1.3.1
а, слева) или
треугольник (D) (рис. 1.3.1
б, слева). Трёхфазная нагрузка (приёмник) также может быть соединена по схеме звезда или треугольник (рис. 1.3.1
а и
б, справа). Электрические величины, относящиеся к генератору, будем снабжать индексами из прописных букв
А,
B и
C, а величины, относящиеся к трёхфазному приёмнику, - индексами из строчных букв
а,
b и
c.
Провода, соединяющие точки А и а, B и b, С и с, называют линейными (провод А, провод B и провод С); соответственно и токи в них IA, IB, IC называют линейными. Провод, соединяющий точку N (нейтраль генератора) с точкой n (нейтральюприёмника) (см. рис. 1.3.1 а), называют нейтральным (иногда, нулевым),а ток IN в нём - током в нейтральном проводе.
1.3.3. Схемы соединения фаз генератора и приёмника звездой. Для упрощения анализа процессов в трёхфазной цепи будем пренебрегать сопротивлениями линейных и нейтрального проводов и считать источники напряжения (рис. 1.3.2, слева) с ЭДС E A, E B и E C идеальными. Напряжения между линейными проводами называют линейными: U AB, U BC, U CA, а между каждым из линейных проводов и нейтральным - фазными: U A, U B, U C генератора и U a, U b, U c приёмника (второй индекс N или n опускают). Условно положительные направления ЭДС, линейных и фазных напряжений и токов в четырёхпроводной схеме звезда-звезда (Y-Y) указаны на рис. 1.3.2.
При принятых допущениях фазные напряжения трёхфазного приёмника в схеме Y-Y с четырьмя проводами (называемой соединением звезда-звезда с нейтральным (нулевым) проводом) равны фазным напряжениям генератора, т. е.
U a = U A, U b = U B, U c = U C,
| Рис. 1.3.2. Четырехпроводная схема соединения генератора и
трехфазного приемника
|
а так называемое
напряжение смещения нейтрали между точками
n и
N равно нулю (
U nN = 0).
Если сопротивления фаз приёмника одинаковые (см. рис. 1.3.2), т. е.


то нагрузка называется симметричной. В этом случае модули фазных токов одинаковые и равны соответствующим линейным токам:
Ia = Ib = Ic = I ф = IА = IВ = IС = I л = U ф /Z ф, (3.1)
где U ф = Ua = Ub = Uc = UA = UB = UC - модули фазных напряжений приёмника и трёхфазного генератора.
| Рис1.3.3. Векторная диаграмма напряжений и токов приёмника при симметричной нагрузке (а) и треугольник фазных и линейного напряжений при соединении фаз
приёмника по схеме звезда (б)
|
На рис. 1.3.3
а приведена векторная диаграмма напряжений и токов трёхфазного приёмника при симметричной нагрузке, носящей активно-ёмкостный характер:

.
Как напряжения  так и токи I a, I b, I c составляют симметричные звёзды, поэтому сумма комплексов фазных токов
так и токи I a, I b, I c составляют симметричные звёзды, поэтому сумма комплексов фазных токов
I N = I a + I b + I c = 0, (3.2)
т. е. ток в нейтральном проводе равен нулю и нейтральный провод можно отключить. В результате получим эквивалентную трёхпроводную систему включения приёмника с генератором по схеме Y-Y.
Для соединения фаз приёмника звёздой (см. рис. 1.3.3 а) очевидно соотношение между линейными и фазными токами:
I ф = I л. (3.3)
Выведем соотношения между линейными и фазными напряжениями для соединения приёмника и генератора по схеме Y-Y (четырёхпроводная схема). Согласно 2ЗК имеем (см. рис. 1.3.2 и рис. 1.3.3 а)
U AB = U A - U B = U ab = Ua - U b,
U BC = U В - U С = U bc = U b - U c,
U CA = U C - U A = U ca = U c - U a .
Если рассмотреть один из треугольников (рис. 1.3.3 б), то легко вывести соотношение между линейным и фазным напряжениями, а именно:

 (3.4)
(3.4)
т. е. фазное напряжение в  раз меньше линейного и отстаёт от него по фазе на угол 30° (точнее, вектор напряжения U a отстаёт по фазе от вектора U ab, вектор U b - от вектора U bc, а вектор U c - от вектора U ca ,, см. рис. 1.3.3 а).
раз меньше линейного и отстаёт от него по фазе на угол 30° (точнее, вектор напряжения U a отстаёт по фазе от вектора U ab, вектор U b - от вектора U bc, а вектор U c - от вектора U ca ,, см. рис. 1.3.3 а).
В четырёхпроводной системе при
несимметричной нагрузке, в которой комплексные сопротивления фаз
Z a ¹ Z b ¹ Z c (например,
Z a = - jX a,
Z b = R b - jXb и
Z c = Rc - - jXc), фазные напряжения приёмника равны соответствующим фазным напряжениям генератора, т. е.
U a = UA, U b = U B, U c = U C,
а фазные токи различны и равны:


 .
.
Ток в нейтральном проводе (рис. 1.3.4)
I N = I a + I b + I c. (3.5)
| Рис. 1.3.5. Схема приёмника (а), векторнные диаграммы напряжений и токов приёмника при нормальной режиме работы (б) и при обрыве фазы «с» (в)
|
Пример 1.3.1. В схеме рис. 1.3.5
а линейное напряжение нагрузки
U л = 380 В. Модули сопротивлений фаз нагрузки равны
Z ф = 110 Ом, но имеют различный характер:
Z a =
R,
Z b =
jXL,
Z с = -
jXC. Найти токи и мощности фаз и приёмника, ток
IN в нейтральном проводе, в том числе и при обрыве фазы «
с».
Решение. 1. Фазные напряжения приёмника:

2. Комплексы токов фаз



3. Построим векторную диаграмму напряжений и токов приёмникa.
В н и м а н и е! При построении векторных диаграмм напряжений и токов в трёхфазной цепи комплексную плоскость поворачивают против хода часовой стрелки на 90° и направляют по оси действительных чисел (вертикально вверх) вектор напряжения U a = Ua = U ф фазы «а» (или комплекс U ab фазы «ab» при соединении фаз приёмника по схеме треугольник). Векторы напряжений  и
и  вычерчивают в комплексной плоскости в соответствии с их аргументами.
вычерчивают в комплексной плоскости в соответствии с их аргументами.
В цепи (см. её схему на рис. 1.3.5 а) ток I а совпадает по фазе с напряжением U a, ток I b отстаёт по фазе от напряжения U b на 90°, а ток I c опережает по фазе напряжение U с на 90° (рис. 1.3.5 б).
4. Комплекс тока в нейтральном проводе равен сумме комплексов фазных токов, т.е.
I N = I а + I b + I c =  =
= 
= 2 + 4×(-0,866) = -1,464 =  A.
A.
5. Комплекс тока в нейтральном проводе при обрыве фазы «с» равен сумме комплексов фазных токов I а и I b, т.е.
I N = I а + I b = 
=  2 - 2×(-0,866) + j 2×0,5 = 0,268 + j = 1,035 ej 75° A.
2 - 2×(-0,866) + j 2×0,5 = 0,268 + j = 1,035 ej 75° A.
6. Векторная диаграмма напряжений и токов приёмника при обрыве фазы «с» представлена на рис. 1.3.5 в).
7. Комплексные мощности фаз приёмника:
S a = U a  = 220 × 2 = 440 B×A (Pa = 440 Вт, Qa = 0),
= 220 × 2 = 440 B×A (Pa = 440 Вт, Qa = 0),
S b = U b  =
=  ×
× 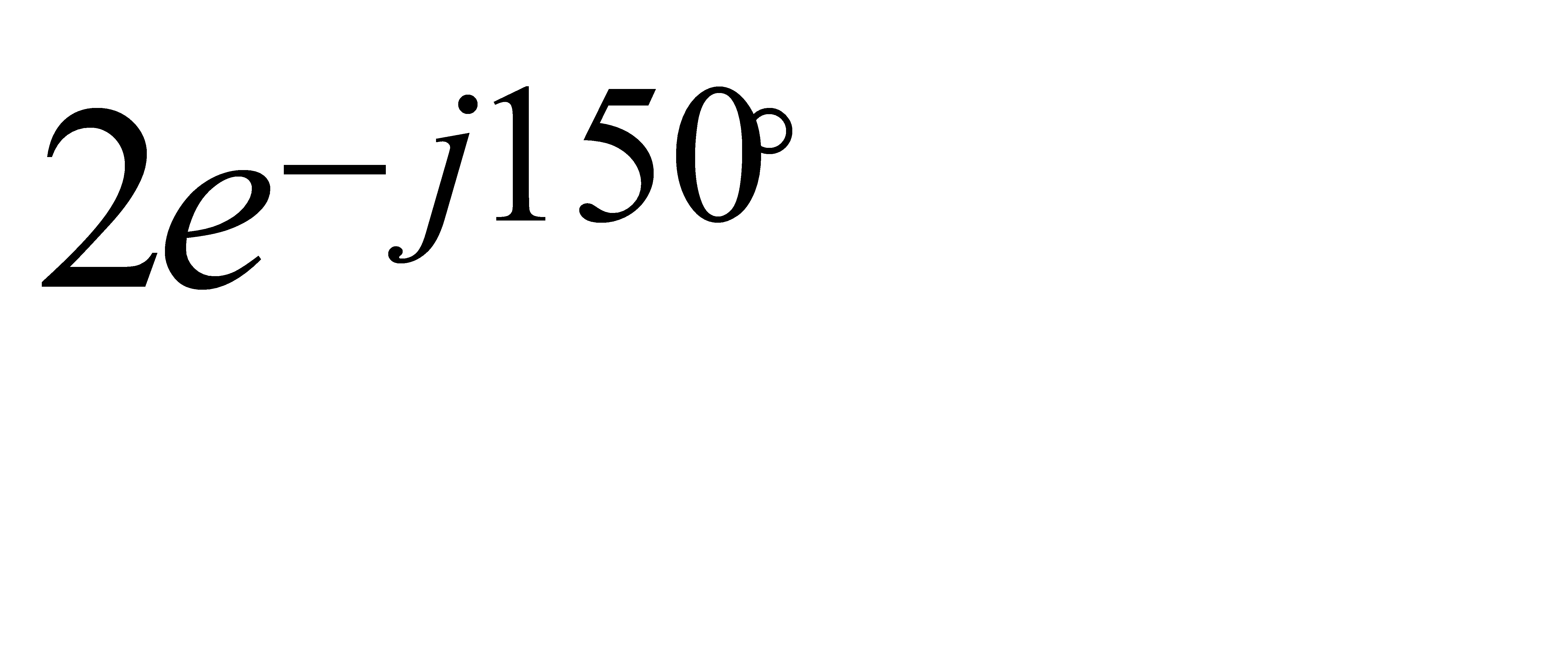
 = 440cos270° - j 440sin270° B×A = j 440 B×A
= 440cos270° - j 440sin270° B×A = j 440 B×A
(Pb = 0, Qb = 440 вар).
S с = U с  =
=  ×
× 
 = 440cos270° + j 440sin270° B×A = - j 440 B×A
= 440cos270° + j 440sin270° B×A = - j 440 B×A
(P с = 0, Q с = - 440 вар).
8. Комплексная мощность приёмника, фазы которого соединены звездой,
S Y = S a + S b + S с = 440 + j 440 - j 440 = 440 B×A (P Y = 440 Вт, Q Y = 0).
2.7.3. Схема соединения фаз генератора и приёмника треугольником. Пусть обмотки трёхфазного генератора и трёхфазный приёмник соединены по схеме треугольник (схема соединения D-D)(рис. 1.3.6). Так как три ЭДС генератора равны по модулю и сдвинуты по фазе на 120° относительно друг друга, то сумма трёх комплексов ЭДС в замкнутом треугольнике А-В-С- A равна нулю, т. е. E AB + E BC + E CA = 0. Поэтому, если к зажимам А, В и С не присоединена нагрузка, то по обмоткам генератора не будет протекать уравнительный ток.
Как видно из рис. 1.3.6, в такой схеме возможно только трёхпроводное соединение трёхфазного приёмника с генератором; последний может быть соединён звездой. На этом же рисунке показаны условно положительные направления линейных и фазных напряжений и токов в системе соединения D-D.
Фазные напряжения приёмника, фазы которого соединёны треугольником, равны соответствующим линейным напряжениям генератора:
U ab = U AB, U bc = U BC,
U ca = U CA, U ф = U л, (3.6)
а модули фазных токов приёмника при симметричной нагрузке
(Z ab = Z bc = Z ca = Z ф = R ф + jX ф):
| Рис. 1.3.6. Схема соединения трехфазного приёмника энергии
с генератором, соединенных по схеме треугольник
|
Iab = Ibc = Ica = I ф = 
. (3.7)
Согласно первому закону Кирхгофа для точек а, b и с (см. рис. П3.6) линейные токи:
I A = I ab - I ca,
I B = I bc - I ab,
I C = I ca - I bc. (3.8)
При симметричной нагрузке комплексы как фазных, так и линейных токов составляют симметричные звёзды (рис. 1.3.7), а соотношение модулей между ними
I л =  I ф, I ф =
I ф, I ф =  , (3.9)
, (3.9)
При несимметричной нагрузке фазные токи различны:
I ab =  I bc =
I bc =  I ca =
I ca =  (3.10)
(3.10)
где 
Линейные токи рассчитывают по формулам (1.3.8). При несимметричной нагрузке линейные токи могут быть как больше, так и меньше фазных токов нагрузки. Заметим, что сумма комплексов линейных токов всегда равна нулю, т. е.
I A + I B + I C = 0. (3.11)
Пример 1.3.2. Трёхфазный потребитель энергии (рис. 1.3.8) с сопротивлениями фаз Z ab = 10 Ом, Z bc = 10 + j 10 =  , Z ca = 10 - j 5 =
, Z ca = 10 - j 5 =  Ом соединён треугольником и включён в трёхфазную сеть с линейным напряжением U л= 380 В.
Ом соединён треугольником и включён в трёхфазную сеть с линейным напряжением U л= 380 В.
Определить фазные и линейные токи, мощности фаз и приёмника и построить векторную диаграмму токов и напряжений, в том числе и при обрыве фазы «b с».
Решение. 1. Комплексы фазных токов:
I ab =  = 38 A,
= 38 A,
I bc = 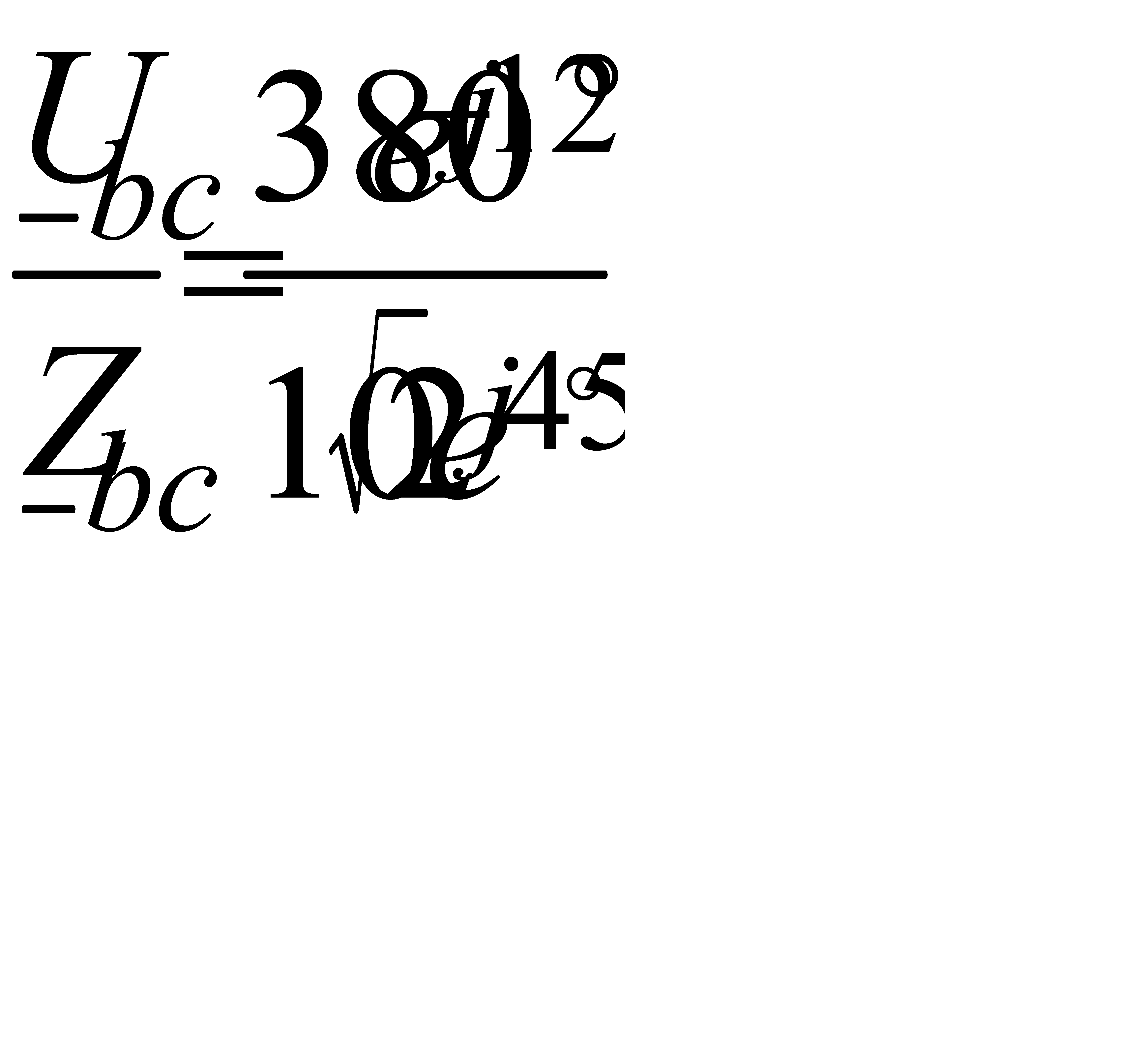
 А,
А,
I ca = 

2. Комплексы линейных токов:
I A = I ab - I ca = 38 - 
I B = I bc - I ab = 

IC = I ca - I bc  -
- 

| Рис. 1.3.8. Схема приёмника энергии (а) и векторные диаграммы напряжений
и токов при нормальной работе (б) и при обрыве фазы «bc» (в)
|
3. Комплексы фазных и линейных токов при обрыве фазы «
bc»:
I ab = 38 A, I bc = 0, I ca 
I A = I ab - I ca =  I B = I bc - I ab = - I ab = -38 A,
I B = I bc - I ab = - I ab = -38 A,
IC = I ca - I bc = I ca 
4. Комплексные мощности фаз:
S ab = U ab  = 380× 38 = 14440 B×A (Pab = 14,44 кВт, Qab = 0),
= 380× 38 = 14440 B×A (Pab = 14,44 кВт, Qab = 0),
S bc = U bc  = 380
= 380  ×
×  = 10220
= 10220  B×A = 10,21
B×A = 10,21  кB×A
кB×A
(Pb с = Sb с cos45° = 10,21 × 0,707 = 7,22 кВт, Qb с = Sb с sin45° = 10,21 × 0,707 = 7,22 квар),
S ca = U ca  = 380
= 380  ×
×  = 12882
= 12882  B×A» 12,88
B×A» 12,88  кB×A
кB×A
(P с a = S с a cos26,5° = 12,88 × 0,895 = 11,53 кВт,
Q с a = - S с a sin26,5° = -12,88 × 0,446 = -5,75 квар),
5. Комплексная мощность, потребляемая приёмником,
S ∆ = S ab + S bc + S ca = 14,44 + 10,21  + 12,88
+ 12,88  =
=
= 14,44 + 7,22 + j 7,22 + 11,53 - j 5,75 = 33,19 + j 1,47 = 33,22  кB×A,
кB×A,
где активная мощность приёмника Р∆ = 33,19 кВт и реактивная индуктивная мощность Q ∆ = 1,47 квар.
6. Векторные диаграммы напряжений и токов потребителя энергии при нормальной работе и при обрыве фазы «bc» приведены на рис. 1.3.8 б и на рис. 1.3.8 в.
Воспользуйтесь поиском по сайту:




 .
.
 так и токи I a, I b, I c составляют симметричные звёзды, поэтому сумма комплексов фазных токов
так и токи I a, I b, I c составляют симметричные звёзды, поэтому сумма комплексов фазных токов
 (3.4)
(3.4) раз меньше линейного и отстаёт от него по фазе на угол 30° (точнее, вектор напряжения U a отстаёт по фазе от вектора U ab, вектор U b - от вектора U bc, а вектор U c - от вектора U ca ,, см. рис. 1.3.3 а).


 .
.



 и
и  вычерчивают в комплексной плоскости в соответствии с их аргументами.
вычерчивают в комплексной плоскости в соответствии с их аргументами. =
= 
 A.
A.
 2 - 2×(-0,866) + j 2×0,5 = 0,268 + j = 1,035 ej 75° A.
2 - 2×(-0,866) + j 2×0,5 = 0,268 + j = 1,035 ej 75° A. = 220 × 2 = 440 B×A (Pa = 440 Вт, Qa = 0),
= 220 × 2 = 440 B×A (Pa = 440 Вт, Qa = 0), =
=  ×
× 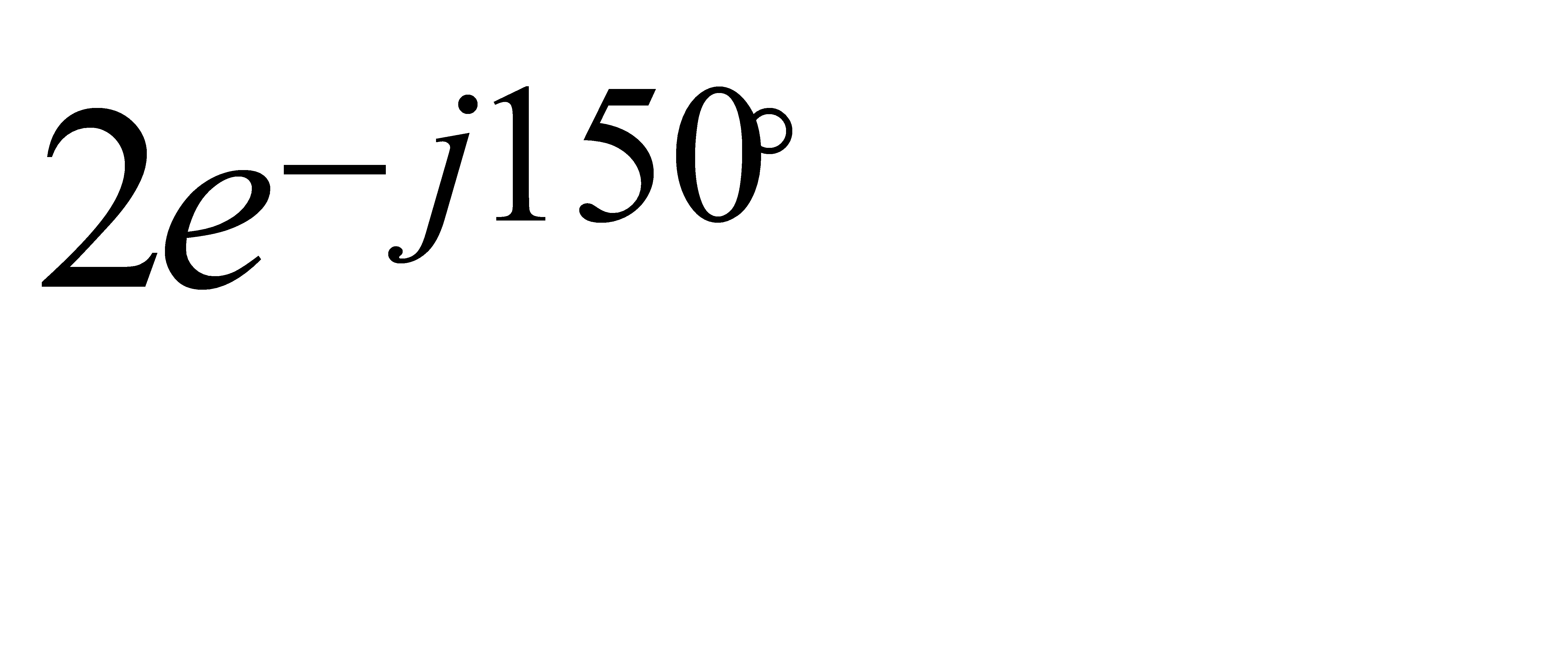
 = 440cos270° - j 440sin270° B×A = j 440 B×A
= 440cos270° - j 440sin270° B×A = j 440 B×A =
=  ×
× 
 = 440cos270° + j 440sin270° B×A = - j 440 B×A
= 440cos270° + j 440sin270° B×A = - j 440 B×A . (3.7)
. (3.7)
 I ф, I ф =
I ф, I ф =  , (3.9)
, (3.9) I bc =
I bc =  I ca =
I ca =  (3.10)
(3.10)
 , Z ca = 10 - j 5 =
, Z ca = 10 - j 5 =  Ом соединён треугольником и включён в трёхфазную сеть с линейным напряжением U л= 380 В.
Ом соединён треугольником и включён в трёхфазную сеть с линейным напряжением U л= 380 В. = 38 A,
= 38 A,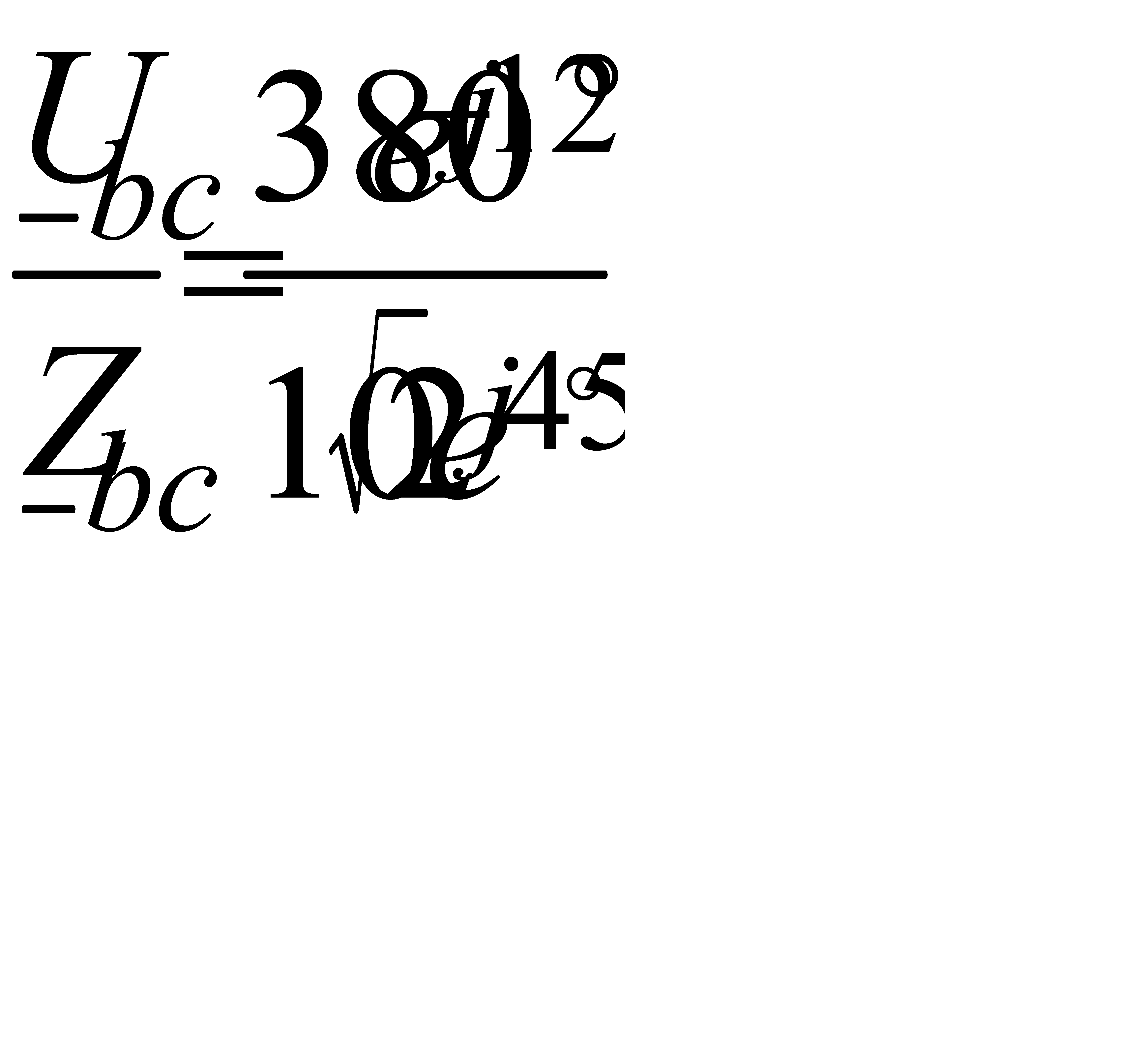
 А,
А,




 -
- 


 I B = I bc - I ab = - I ab = -38 A,
I B = I bc - I ab = - I ab = -38 A,
 = 380× 38 = 14440 B×A (Pab = 14,44 кВт, Qab = 0),
= 380× 38 = 14440 B×A (Pab = 14,44 кВт, Qab = 0), = 380
= 380  ×
×  = 10220
= 10220  B×A = 10,21
B×A = 10,21  кB×A
кB×A = 380
= 380  ×
×  = 12882
= 12882  B×A» 12,88
B×A» 12,88  кB×A
кB×A + 12,88
+ 12,88  =
= кB×A,
кB×A,

