 |
Способы моделирования.
|
|
|
|
1.4.1. Теория подобия.
— Теория подобия и размерностей представляет собой основу физического моделирования.
— Прежде всего, договоримся критериями подобия считать числа подобия, составленные из условий однозначности. Следовательно, если задачей расчета является нахождение коэффициента теплоотдачи при заданной скорости движения теплоносителя, то определяться будет число подобия Nu (число Нуссельта), а задаваться будут критерии подобия Re или Pe, Gr, Pr (критерии Рейнольдса или Пекле, Грасгофа, Прандля). Если же задача формулируется так: при каком значении скорости теплоносителя можно получить заданное значение коэффициента теплоотдачи, то число Нуссельта превращается в критерий подобия, а критерий Рейнольдса перестает быть критерием подобия, а становится лишь числом подобия.
— Обычно критериальные уравнения формируются как степенные модели, что вызвано тем обстоятельством, что при логарифмировании они превращаются в линейные. Вид критериального уравнения теоретически никак не обосновывается, обосновывается лишь ассортимент критериев подобия, входящих в него.
— Рассмотрим три основных уравнения сохранения для одномерного случая. Каждое такое уравнение будет включать в себя следующие составляющие:
| Локальное изменение | + | Конвективное изменение | + | Диффузионное изменение | + | Изменение за счет производства | = |
при наличии граничных условий.
— Уравнение сохранения массы:

| 
|
где с – концентрация, t – время, v – скорость, х – линейная координата, D – коэффициент диффузии, r – скорость реакции на единицу объема, r=kc, r=kc2 и т.д., km – коэффициент массопереноса, а – поверхность на единицу объема.
|
|
|
— Уравнение сохранения энергии:

| 
|
где Cp – теплоемкость, r – плотность, Т – температура, l – теплопроводность, q – скорость образования тепла на единицу объема, a – коэффициент теплоотдачи.
— Уравнение сохранения момента:

| 
|
где m – динамическая вязкость, f – сила на единицу объема, t – напряжение сдвига, g – поверхностное натяжение, l – длина на единицу объема.
— Формирование чисел подобия легко осуществляется "делением" одного столбца на другой
— Отношение конвективного изменения к диффузионному изменению:
| Масса | 
| Боденштейн |
| Энергия | 
| Пекле |
| Момент | Re 
| Рейнольдс |
— Отношение изменения за счет производства к конвективному изменению:
| Масса | 
| Дамкелер |
| Энергия | 
| Дамкелер |
| Момент | 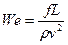
| Вебер |
— Отношение соотношения для граничных условий к конвективному изменению:
| Масса | 
| Меркель |
| Энергия | 
| Стентен |
| Момент | 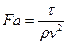
| Фанниган |
— Отношение изменения за счет производства к диффузионному изменению:
| Масса |  
| Дамкелер |
| Энергия | 
| Дамкелер |
| Момент | 
| Пуазейль |
— Отношение соотношения для граничных условий к диффузионному изменению:
| Масса | 
| Шервуд |
| Энергия | 
| Нуссельт |
| Момент | 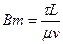
| Бингам |
— Отношение диффузионного изменения к локальному изменению:
| Энергия | 
| Фурье |
— Кроме того:
| Le=Bo/Pe | 
| Льюис |
| Sc=Bo/Re | 
| Шмидт |
| Pr=Pe/Re | 
| Прандтль |
— Напоминание: коэффициент теплоотдачи является функцией большого количества переменных – геометрических характеристик, температуры, скорости, вязкости, плотности, теплопроводности, теплоемкости, коэффициента теплового расширения и пр. Соотношение, характеризующее эту зависимость, будет громоздким и будет различным для каждой жидкости. Теория подобия позволяет получить общее решение для всех жидкостей и снижает размерность, т.н. уменьшает количество факторов.
— Вместо a = f(d, l, T, w, m, r, l, Cp, b,…) получим Nu = j (Re, Gr, Pr).
— В случае процессов физико-химических превращений используются критерии теплового и материального обмена. Кроме критерия Рейнольдса и Вебера необходимо упомянуть критерий Фруда Fr=gL/v2 (он необходим, если f – сила тяжести) и критерий Грасгофа Gr=bgDTl3/n2 (если f – подъемная сила).
|
|
|
— Критерий гомохронности получается как отношение конвективного изменения к локальному изменению независимо от того, какое уравнение сохранения рассматривается: Ho=vt/L.
— Особое значение имеет критерий контакта, который получается из уравнения кинетики необратимой реакции произвольного порядка:

|
Дифференцируя это выражение, получим:

|
— Отсюда критерий контакта:
Ko=knZn–1t,
где Z – изменение суммарного теплового эффекта Dqсум, изменение крутящего момента DМ, изменение количества узлов сетки Dn, изменение концентрации прореагировавшего реагента Dс.
— Критерий контакта следует понимать как меру отношения скоростей обусловливающих процессов обмена к внутренней скорости самого превращения. Критерий Ко прямо пропорционален времени контакта и обратно пропорционален времени распада исходных продуктов.
— В частном случае для реакции первого порядка при n=1 Ko=kt. Критерий kt называется кинетическим критерием.
1.4.2. Теория соответственных состояний.
— В классической термодинамике при анализе поведения реальных газов используют недостаточно точное, но простое в интерпретации уравнениеВан-дер-Ваальса:

В этом уравнении p, v и Т – соответственно, давление, удельный объем и температура, a и b – константы, R – газовая постоянная. Уравнение выведено с учетом влияния конечности объема молекул газа (константа b), а также наличия сил взаимного притяжения между молекулами (член a/v2). Значения констант существенно отличаются друг от друга для различных газов. Между параметрами критического состояния (pk, vk и Тk) и коэффициентами уравнения Ван-дер-Ваальса a и b существует связь: vk=3b, pk,=a/27b2, Тk=8a/27bR. Вводя приведенные параметры p=p/pk, j=v/vk, t=T/Tk, можно получить приведенное уравнение Ван-дер-Ваальса, справедливое для группы термодинамически подобных веществ:

— Описанный подход может быть использован, например, при интерпретации результатов получения кривой напряжение–деформация. В этом случае в качестве приведенной деформации следует рассматривать значение удлинения, отнесенное к относительному удлинению при разрыве, а в качестве приведенного напряжения – отношение напряжения при данном удлинении к прочности при растяжении.
|
|
|
1.4.3. Метод аналогий.
— В этом методе, в отличие от теории подобия, рассматриваются и сопоставляются различные по своей физической природе процессы.
— Приведем несколько примеров:

| Уравнение Дарси-Вейсбаха, характеризующее взаимосвязь скорости фильтрации w и градиента давления, k – коэффициент фильтрации. |

| Уравнение Ньютона, характеризующее взаимосвязь напряжения сдвига t и градиента скорости, m – динамическая вязкость. |

| Закон Био-Фурье, характеризующий взаимосвязь теплового потока q и градиента температуры, l – теплопроводность. |

| Первый закон Фика, характеризующий взаимосвязь потока массы m и градиента концентрации, D – коэффициент диффузии. |

| Закон Ома, характеризующий взаимосвязь силы тока i и градиента напряжения, k – электрическая проводимость. |
— Все эти соотношения в левой части содержат векторную величину, которую можно определить как обобщенный заряд, который самопроизвольно распространяется в направлении убывания, сопряженного с ним вектора обобщенного потенциала. Коэффициент пропорциональности, ставящий в соответствие два вектора, представляет собой тензор второго ранга.
— Аналогичным образом могут быть записаны дифференциальные уравнения второго порядка в частных производных (запишем их для простоты без внутренних источников):

| Второй закон Фика, уравнение диффузии. |

| Уравнение Фурье, дифференциальное уравнение теплопроводности. |

| Уравнение Навье-Стокса, основное реологическое соотношение. |

| Телеграфное уравнение, распределение напряжений в цепи емкостей и сопротивлений. |
— Нетрудно видеть, что все эти уравнения одинаковые с формальной точки зрения; они могут рассматриваться как частный случай общего уравнения, называемого гипергеометрическим уравнением Гильберта. На этой аналогии строятся подходы, развиваемые в кибернетике, и основанные на применении аналоговых машин. Например, в случае анализа температурного поля с использованием поля напряжений для интерпретации полученных результатов, требуется, чтобы критерий Фурье тепловой Fo=at/L2 был равен соответствующему критерию электрического поля P=t/RCL2. Воистину прав был сказавший: "Математика – это искусство давать одно и то же имя разным объектам".
|
|
|
1.4.4. Метод асимптотической коррекции.
— Целью этого метода является замена множества кривых одной кривой с использованием преобразования осей координат.
 |
— В качестве примера рассмотрим зависимость семейства ломанных линий F=F(р) при различных значениях (a, b, c, d) другой независимой переменной. После этого строим зависимость отклика F от этой второй переменной при р=0 (F') и при р=р' (F"). Получаем эмпирические формулы для этих двух кривых с использованием метода наименьших квадратов (МНК-оценки). Строим, наконец, результирующую ломанную линию, откладывая по оси абсцисс р/р', а по оси ординат f=(F-F')/(F"-F').
— Таким образом можно интерпретировать интегральные кинетические кривые, рассматривая по оси ординат степень превращения, а по оси абсцисс – отношение времени к абсциссе перегиба на интегральной кривой, медиане или математическому ожиданию.
|
|
|


