Закон Гука при растяжении и сжатии

Напряжения и деформации при растяжении и сжатии связаны между собой линейной зависимостью, которая называется законом Гука, по имени английского физика Р. Гука (1653-1703 г.г.), установившего этот закон.
Сформулировать закон Гука можно так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.

Математически эта зависимость записывается так:

σ = E ε.

Здесь Е – коэффициент пропорциональности, который характеризует жесткость материала бруса, т. е. его способность сопротивляться деформации; его называют модулем продольной упругости, или модулем упругости первого рода.
Модуль упругости, как и напряжение, выражаются в паскалях (Па).

Значения Е для различных материалов устанавливаются экспериментально-опытным путем, и их величину можно найти в соответствующих справочниках.
Так, для стали Е = (1,96.…2,16) х 105 МПа, для меди Е = (1,00...1,30) х 105 МПа и т. д.

Следует оговориться, что закон Гука справедлив лишь в определенных пределах нагружения.
Если в формулу закона Гука подставить полученные ранее значения относительного удлинения и напряжения: ε = Δl / l, σ = N / А, то можно получить следующую зависимость:

Δl = N l / (E А).

Произведение модуля упругости на площадь сечения Е × А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.

Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение Е А / l называют жесткостью бруса при растяжении и сжатии.

Приведенные выше формулы закона Гука справедливы лишь для брусьев и их участков, имеющих постоянное поперечное сечение, изготовленных из одного материала и при постоянной силе. Для бруса, имеющего несколько участков, отличающихся материалом, размерами сечения, продольной силой, изменение длины всего бруса определяется, как алгебраическая сумма удлинений или укорочений отдельных участков:

Δl = Σ (Δl_i)

 

 

Деформация

Деформация (англ. deformation) - это изменение формы и размеров тела (или части тела) под действием внешних сил, при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела. При увеличении напряжения деформация может закончиться разрушением. Способность материалов сопротивляться деформации и разрушению под воздейстивем различного вида нагрузок характеризуется механическими свойствами этих материалов.

На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преобладающим действием касательной составляющей напряжения, другие - с действием его нормальной составляющей.

Виды деформации

По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:

• Деформация растяжения;
• Деформация сжатия;
• Деформация сдвига (или среза);
• Деформация при кручении;
• Деформация при изгибе.

К простейшим видам деформации относятся: деформация растяжения, деформация сжатия, деформация сдвига. Выделяют также следующие виды деформации: деформация всестороннего сжатия, кручения, изгиба, которые представляют собой различные комбинации простейших видов деформации (сдвиг, сжатие, растяжение), так как сила приложенная к телу, подвергаемому деформации, обычно не перпендикулярна его поверхности, а направлена под углом, что вызывает как нормальные, так и касательные напряжения. Изучением видов деформации занимаются такие науки, как физика твёрдого тела, материаловедение, кристаллография.

В твёрдых телах, в частности - металлах, выделяют два основных вида деформаций - упругую и пластическую деформацию, физическая сущность которых различна.

 

Сдвигом называют такой вид деформации, когда в поперечных сечениях возникают только перерезывающие силы. Такое напряженное состояние соответствует действию на стержень двух равных противоположно направленных и бесконечно близко расположенных поперечных сил (рис. 2.13, а, б), вызывающих срез по плоскости, расположенной между силами.

 

Рис. 2.13. Деформация и напряжения при сдвиге

 

Срезу предшествует деформация – искажение прямого угла между двумя взаимно-перпендикулярными линиями. При этом на гранях выделенного элемента (рис. 2.13, в) возникают касательные напряжения. Величина смещения граней называется абсолютным сдвигом. Значение абсолютного сдвига зависит от расстояния h между плоскостями действия сил F. Более полно деформацию сдвига характеризует угол , на который изменяются прямые углы элемента – относительный сдвиг:

. (2.27)

 

Используя ранее рассмотренный метод сечений, легко убедиться, что на боковых гранях выделенного элемента возникают только перерезывающие силы Q=F, являющиеся равнодействующими касательных напряжений:

 

. (2.28)

 

Принимая во внимание, что касательные напряжения распределены равномерно по поперечному сечению А, их значение определяется соотношением:

 

. (2.29)

 

Экспериментально установлено, что в пределах упругих деформаций величина касательных напряжений пропорциональна относительному сдвигу (закон Гука при сдвиге):

 

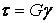, (2.30)

 

где G – модуль упругости при сдвиге (модуль упругости второго рода).

Между модулями продольной упругости и сдвига существует взаимосвязь

 

,

 

где – коэффициент Пуассона.

Приближенные значения модуля упругости при сдвиге, МПа: сталь – 0,8·10⁵; чугун – 0,45·10⁵; медь – 0,4·10⁴; алюминий – 0,26·10⁵; резина – 4.

 

2.4.1.1. Расчеты на прочность при сдвиге

Чистый сдвиг в реальных конструкциях реализовать крайне сложно, так как вследствие деформации соединяемых элементов происходит дополнительный изгиб стержня, даже при сравнительно небольшом расстоянии между плоскостями действия сил. Однако в ряде конструкций нормальные напряжения в сечениях малы и ими можно пренебречь. В этом случае условие прочностной надежности детали имеет вид:

 

, (2.31)

 

где – допускаемые напряжение на срез, которые обычно назначают в зависимости от величины допускаемого напряжения при растяжении:

– для пластичных материалов при статической нагрузке =(0,5…0,6) ;

– для хрупких – =(0,7 … 1,0) .

 

2.4.1.2. Расчеты на жесткость при сдвиге

Они сводятся к ограничению упругих деформаций. Решая совместно выражение (2.27)–(2.30), определяют величину абсолютного сдвига:

 

, (2.32)

 

где 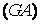– жесткость при сдвиге.

 

Кручение

2.4.2.1. Построение эпюр крутящих моментов

2.4.2.2. Деформации при кручении

2.4.2.3. Напряжения при кручении

2.4.2.4. Геометрические характеристики сечений

2.4.2.5. Расчеты на прочность и жесткость при кручении

 

Кручением называют такой вид деформации, когда в поперечных сечениях возникает единственный силовой фактор – крутящий момент.

Деформация кручения происходит при нагружении бруса парами сил, плоскости действия которых перпендикулярны к его продольной оси.

 

2.4.2.1. Построение эпюр крутящих моментов

Для определения напряжений и деформаций бруса строят эпюру крутящих моментов, показывающую распределение крутящих моментов по длине бруса. Применив метод сечений и рассмотрев в равновесии любую часть, станет очевидно, что момент внутренних сил упругости (крутящий момент ) должен уравновесить действие внешних (вращающих) моментов на рассматриваемую часть бруса. Принято момент считать положительным, если наблюдатель смотрит на рассматриваемое сечение со стороны внешней нормали и видит вращающий момент Т, направленным против хода движения часовой стрелки. При противоположном направлении моменту приписывается знак минус.

Например, условие равновесия для левой части бруса имеет вид (рис. 2.14):

– в сечении А-А:

; ,

– в сечении Б-Б:

.

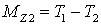Границами участков при построении эпюры являются плоскости действия вращающих моментов .

 

 

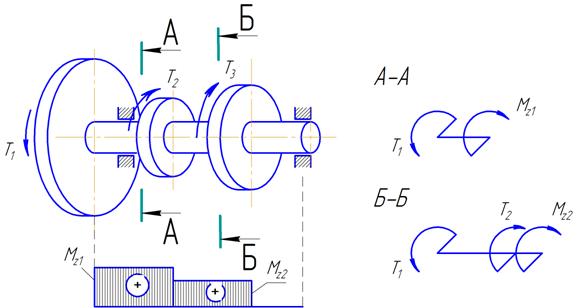
Рис. 2.14. Расчетная схема бруса (вала) при кручении

 

2.4.2.2. Деформации при кручении

Если на боковую поверхность стержня круглого поперечного сечения нанести сетку (рис. 2.15, а) из равноотстоящих окружностей и образующих, а к свободным концам приложить пары сил с моментами Т в плоскостях, перпендикулярных к оси стержня, то при малой деформации (рис. 2.15, б) можно обнаружить:

 

 

Рис. 2.15. Схема деформации при кручении

 

· образующие цилиндра превращаются в винтовые линии большого шага;

· квадраты, образованные сеткой, превращаются в ромбы, т.е. происходит сдвиг поперечных сечений;

· сечения, круглые и плоские до деформации, сохраняют свою форму и после деформации;

· расстояние между поперечными сечениями практически не изменяется;

· происходит поворот одного сечения относительно другого на некоторый угол.

На основании этих наблюдений теория кручения бруса основана на следующих допущениях:

· поперечные сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и после деформации;

· равноотстоящие поперечные сечения поворачиваются относительно друг друга на равные углы;

· радиусы поперечных сечений в процессе деформации не искривляются;

· в поперечных сечениях возникают только касательные напряжения. Нормальные напряжения малы. Длину бруса можно считать неизменной;

· материал бруса при деформации подчиняется закону Гука при сдвиге: .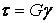

В соответствии с этими гипотезами кручение стержня круглого поперечного сечения представляют как результат сдвигов, вызванных взаимным поворотом сечений.

На стержне круглого поперечного сечения радиусом r, заделанным одним концом и нагруженным вращающим моментом Т на другом конце (рис. 2.16, а), обозначим на боковой поверхности образующую АD, которая под действием момента займет положение АD₁. На расстоянии Z от заделки выделим элемент длиной dZ. Левый торец этого элемента в результате кручения повернется на угол , а правый – на угол ( ). Образующая ВС элемента займет положение В₁С₁, отклонившись от исходного положения на угол . В силу малости этого угла

 

.

 

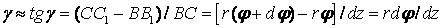Отношение 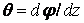представляет угол закручивания единицы длины стержня и называется относительным углом закручивания. Тогда

 

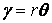. (2.33)

 

 

Рис. 2.16. Расчетная схема определения напряжений
при кручении стержня круглого поперечного сечения

 

2.4.2.3. Напряжения при кручении

Принимая во внимание (2.33), закон Гука при кручении можно описать выражением:

 

. (2.34)

 

В силу гипотезы, что радиусы круглых поперечных сечений не искривляются, касательные напряжения сдвига в окрестностях любой точки тела, находящейся на расстоянии 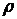от центра (рис. 2.16, б), равны произведению

 

, (2.35)

 

т.е. пропорциональны расстоянию ее до оси.

Значение относительного угла 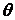закручивания по формуле (2.35) может быть найдено из условия, что элементарная окружная сила ( ) на элементарной площадке размером dA, расположенной на расстоянии 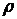от оси бруса, создает относительно оси элементарный момент (рис. 2.16, б):

 

.

 

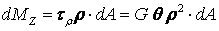Сумма элементарных моментов, действующих по всему поперечному сечению А, равна крутящему моменту М_Z. Считая, что :

.

Интеграл представляет собой чисто геометрическую характеристику и носит название полярного момента инерции сечения.

Таким образом,

 

, (2.36)

 

откуда, угол закручивания единицы длины бруса

 

. (2.37)

 

Произведение называется жесткостью сечения бруса при кручении.

Полный угол закручивания, рад:

 

. (2.38)

 

Если крутящий момент и момент инерции сечения постоянны по длине стержня, то полный угол закручивания

 

. (2.39)

 

Решив совместно выражения (2.35) и (2.36), получим уравнение

 

, (2.40)

 

из которого следует, что напряжение в точке поперечного сечения прямо пропорционально расстоянию до центра сечения. При . Наибольшие напряжения возникают у наружной поверхности: .

Отношение полярного момента инерции к наибольшему радиусу r называется моментом сопротивления сечения кручению , мм³:

 

. (2.41)

 

Условие прочности принимает вид

 

 

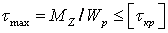
Закон Гука при сдвиге

Материалы о физике / Основы сопротивления материалов / Закон Гука при сдвиге

Для определения зависимости между нагрузкой и деформацией при сдвиге проводят испытания материала на кручение. При данном испытании строится диаграмма сдвига 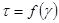(график зависимости между касательным напряжением и относительным сдвигом). Более подробное описание испытания на кручение образцов цилиндрической формы приведено в методических указаниях к лабораторным работам

Для пластичных материалов диаграмма сдвига аналогична диаграмме растяжения (рис. 4.5).

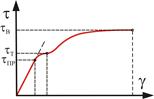
Рис. 4.5

При рассмотрении деформации образца в пределах упругости видна линейная зависимость между относительным сдвигом и касательным напряжением.

(4.23)

где - коэффициент пропорциональности, который называется модулем упругости при сдвиге или модулем упругости второго рода.

Зависимость (4.23) выражает закон Гука при сдвиге.

Между величинами модуля продольной упругости и модуля упругости при сдвиге для одного и того же материала существует зависимость

(4.24)

При значении коэффициента Пуассона получим, что

Запишем выражение для перемещения одной грани относительно другой (абсолютного сдвига (рис. 4.1)) при чистом сдвиге. Обозначая площадь грани , равнодействующую сдвигающую силу и расстояние между сдвигаемыми гранями 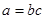(рис. 4.1), получим

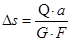(4.25)

Формула (4.25) выражает закон Гука для абсолютного сдвига.

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: