 |
Нормальные напряжения при чистом изгибе
|
|
|
|
Как было установлено ранее, в поперечных сечениях балки при чистом изгибе возникают только нормальные напряжения растяжения и сжатия. Вопрос о распределении этих напряжений по поперечному сечению решается путем рассмотрения деформаций волокон балки.
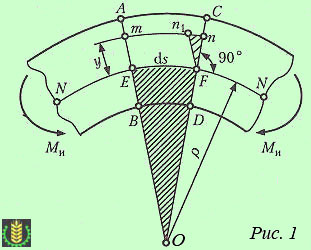
Рассмотрим участок балки, подверженный деформации чистого изгиба. Двумя поперечными сечениями АВ и СD выделим элемент балки бесконечно малой длины ds (рис 1). Радиус кривизны нейтрального слоя балки обозначим ρ.
Рассмотрим слой волокон mn, находящийся на расстоянии y от нейтрального слоя NN. Это волокно в результате деформации изгиба удлинилось на величину nn1. Ввиду малости расстояния ds заштрихованные треугольники будем считать прямолинейными; эти треугольники подобны (n1F || mE):
Δ OEF ~ Δ Fnn1.
Из подобия треугольников запишем равенство:
nn1 / ds = y / ρ.
Так как левая часть этого равенства есть относительное удлинение, т. е. nn1 / ds = ε, то y / ρ = ε.
Применив закон Гука при растяжении и сжатии σ = Еε, получим:
σ = Еy / ρ.
Из этой формулы видно, что нормальные напряжения при изгибе распределены по высоте сечения неравномерно: максимальные напряжения возникают в волокнах, наиболее удаленных от нейтральной оси. По ширине сечения нормальные напряжения не меняются.
Распределение нормальных напряжений изображено на рис. 2.
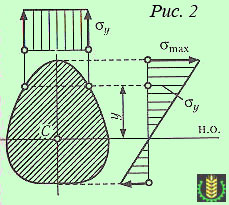
Полученная формула для определения нормальных напряжений неудобна, так как в нее входит радиус кривизны нейтрального слоя.
Для вывода формулы, связывающей нормальные напряжения с изгибающим моментом, применим метод сечений и рассмотрим равновесие части балки, изображенной на рис. 3.
В плоскости поперечного сечения выделим бесконечно малую площадку dA, в пределах которой будем считать нормальные напряжения σ постоянными; тогда нормальная сила dN, действующая на площадку dA, будет равна:
|
|
|
dN = σdA.
Составим уравнения равновесия:
1. Σ Z = 0; ∫ dN = 0, или: ∫ σ dA = ∫ Еy / ρ dA = Е / ρ ∫ y dA = 0.
(ρ для данного сечения, а также модуль упругости Е – величины постоянные, поэтому вынесены за знак интеграла). Поскольку ρ и Е не равны нулю, значит, ∫ y dA = 0. Этот интеграл представляет собой статический момент площади сечения относительно оси x, т. е. нейтральной оси бруса (балки). Равенство нулю статического момента инерции означает, что при изгибе нейтральная ось проходит через центр тяжести площади поперечного сечения;
2. Σ Ми = 0; - m + ∫ y dN = 0.
Так как при чистом изгибе изгибающий момент равен внешнему моменту Ми = m, то
Ми = ∫ y dN = ∫ y dA = ∫ y Еy / ρ dA = Е / ρ ∫ y2 dA,
откуда:
Ми = Е I / ρ,

где: I = ∫ y2 dA – момент инерции поперечного сечения относительно нейтральной оси; ЕI – жесткость сечения при изгибе.
Так как при чистом изгибе балки постоянного сечения Ми = const, то:
ρ = EI / Ми = const.
Следовательно, изогнутая ось такой балки представляет собой дугу окружности. Выражение радиуса кривизны подставим в формулу для определения нормальных напряжений; тогда:
σ = Еy / ρ = Ey / EI / Ми = Ми y / I.
Максимальное значение нормальные напряжения будут иметь у волокон, наиболее удаленных от нейтральной оси:
σmax = Ми ymax / I = Ми / I / ymax = Ми / W,
где W = I / ymax – момент сопротивления изгибу (или осевой момент сопротивления).
Момент сопротивления изгибу есть отношение осевого момента инерции поперечного сечения относительно нейтральной оси к расстоянию от этой оси до наиболее удаленного волокна.
Единица момента сопротивления сечения изгибу [W] = м3.
Итак, наибольшие нормальные напряжения при чистом изгибе вычисляются по формуле
σmax = Ми / W.
Нетрудно заметить, что эта формула по своей структуре аналогична формулам для определения напряжений при растяжении, сжатии, сдвиге и кручении.
|
|
|
***


|
|
|


