 |
Классификация зубчатых передач
|
|
|
|
Зубчатые передачи классифицируются по ряду конструктивных признаков и особенностей.
В зависимости от взаимного расположения осей, на которых размещены зубчатые колеса, различают передачи цилиндрические (при параллельных осях), конические (при пересекающихся осях) и винтовые (при перекрещивающихся осях).
Винтовые зубчатые передачи применяются ограниченно, поскольку имеют низкий КПД из-за повышенного скольжения в зацеплении и низкую нагрузочную способность. Тем не менее, они имеют и некоторые достоинства – высокую плавность хода и возможность выводить концы валов за пределы передачи в обе стороны.
На рисунке 1 представлены наиболее широко применяемые виды зубчатых передач:
1 - цилиндрическая прямозубая передача;
2 - цилиндрическая косозубая передача;
3 - шевронная передача;
4 - реечная передача;
5 - цилиндрическая передача с внутренним зацеплением;
6 - винтовая передача;
7 - коническая прямозубая передача;
8 - коническая косозубая передача;
9 - коническая передача со спиралевидными зубьями;
10 - гипоидная передача.
В зависимости от вида передаваемого движения различают зубчатые передачи, не преобразующие передаваемый вид движения и преобразующие передаваемый вид движения. К последним относятся реечные зубчатые передачи, в которых вращательное движение преобразуется в поступательное или наоборот. В таких передачах рейку можно рассматривать, как зубчатое колесо с бесконечно большим диаметром.
Среди перечисленных видов зубчатых передач наиболее распространены цилиндрические передачи, поскольку они наиболее просты в изготовлении и эксплуатации, надежны и имеют небольшие габариты.
В зависимости от расположения зубьев на ободе колес различают передачи прямозубые, косозубые, шевронные и с круговыми (спиральными) зубьями.
Шевронные зубчатые колеса можно условно сравнивать со спаренными косозубыми колесами, имеющими противоположный угол наклона зубьев. Такая конструкция позволяет избежать осевых усилий на валы и подшипники опор, неизбежно появляющихся в обычных косозубых передачах.
|
|
|
В зависимости от формы профиля зубьев различают эвольвентные зубчатые передачи и передачи с зацеплением Новикова.
Эвольвентное зацепление в зубчатых передачах, предложенное еще в 1760 году российским ученым Леонардом Эйлером, имеет наиболее широкое распространение.
В 1954 году в России М. Л. Новиков предложил принципиально новый тип зацеплений в зубчатых колесах, при котором профиль зуба очерчен дугами окружностей. Такое зацепление возможно лишь для косых зубьев.
В принципе, возможно изготовление зубчатых передач и с другими формами зубьев – даже квадратными, треугольными или трапецеидальными. Но такие передачи имеют ряд существенных недостатков (непостоянство передаточного отношения, низкий КПД и т. д.), поэтому распространения не получили. В приборах и часовых механизмах иногда встречаются зубчатые передачи с циклоидальным зацеплением.
В зависимости от взаимного положения зубчатых колес передачи бывают с внешним и внутренним зацеплением. Наиболее распространены передачи с внешним зацеплением.
В зависимости от конструктивного исполнения различают закрытые и открытые зубчатые передачи. В закрытых передачах колеса помещены в пыле- и влагонепроницаемые корпуса (картеры) и работают в масляных ваннах (зубчатое колесо погружают в масло до 1/3 радиуса).
В открытых передачах зубья колес работают всухую или при периодическом смазывании консистентной смазкой и не защищены от вредного воздействия внешней среды.
В зависимости от числа ступеней зубчатые передачи бывают одно- и многоступенчатые.
|
|
|
В зависимости от относительного характера движения осей зубчатых колес различают рядовые передачи, у которых оси неподвижны, и планетарные зубчатые передачи, у которых ось сателлита вращается относительно центральных осей.
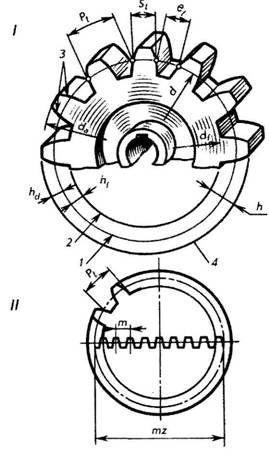
Рис. 178
Основные параметры зубчатых колес:
1. Делительными окружностями пары зубчатых колес называются соприкасающиеся окружности, катящиеся одна по другой без скольжения. Эти окружности, находясь в зацеплении (в передаче), являются сопряженными. На чертежах диаметр делительной окружности обозначают буквой d.
2. Окружной шаг зубьев Рt — расстояние (мм) между одноименными профильными поверхностями соседних зубьев. Шаг зубьев, как нетрудно представить, равен делительной окружности, разделенной на число зубьев z.
3. Длина делительной окружности. Модуль. Длину делительной окружности можно выразить через диаметр и число зубьев: Пd = Pt • r. Отсюда диаметр делительной окружности d = (Рt • z)/П.
Отношение Pt/П называется модулем зубчатого зацепления и обозначается буквой т. Тогда диаметр делительной окружности можно выразить через модуль и число зубьев d = m • z. Отсюда m = d/z.
Значение модулей для всех передач — величина стандартизированная.
Для понимания зависимости между величинами Рt т и d приведена схема на рис. 178, II, где условно показано размещение всех зубьев 2 колеса по диаметру ее делительной окружности в виде зубчатой рейки.
4. Высота делительной головки зуба ha — расстояние между делительной окружностью колеса и окружностью вершин зубьев.
5. Высота делительной ножки зуба hf — расстояние между делительной окружностью колеса и окружностью впадин.
6. Высота зуба h — расстояние между окружностями вершин зубьев и впадин цилиндрического зубчатого колеса h = ha + hf..
7. Диаметр окружности вершин зубьев da — диаметр окружности, ограничивающей вершины головок зубьев.
8. Диаметр окружности впадин зубьев df — диаметр окружности, проходящей через основания впадин зубьев.
При конструировании механизма конструктор рассчитывает величину модуля т для зубчатой передачи и, округлив, подбирает модуль по таблице стандартизированных величин. Затем он определяет величины остальных геометрических элементов зубчатого колеса.
|
|
|
Зубчатыми называют механизмы (передачи), в которых движение между звеньями передается с помощью последовательно зацепляющихся зубьев. Простейший зубчатый механизм (рис. 1.32) состоит из двух звеньев (зубчатые колеса), соединенных со стойкой вращательными парам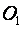и 
и 
(низшими) пятого класса и образующими между собой пару 
(высшую) четвертого класса. Зубчатые механизмы являются наиболее распространенным в машиностроении и приборостроении видом передач благодаря существенным достоинствам: компактности, высокой надежности в широком диапазоне мощностей (до 150 МВт) и скоростей (до 275 м/c), высокому КПД, простоте ухода, обеспечению высокой точности передаточного отношения, сравнительно малым нагрузкам на валы и опоры. Недостатки передач обусловлены высокой трудоёмкостью изготовления колес, относительно высоким требованием к точности изготовления и монтажа, возможностью появления шума при работе на больших скоростях.
Основы теории зацепления
Для обеспечения постоянства передаточного отношения: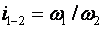 
необходимо, чтобы профили сопряженных зубьев были очерчены такими кривыми, которые удовлетворяли бы требованиям основной теоремы зацепления
Рассмотрим связь между угловыми скоростями двух звеньев (рис. 1.32), образующих высшую пару. Профили П1 и П2, жестко связанные со звеньями 1 и 2, вращаются с угловыми скоростями w1 и w2 относительно неподвижных точек О1 и О2, расположенных друг от друга на расстоянии аw.
Проведем через точку С касания профилей общую к ним нормаль N-N и касательную К-К. Из центров вращения звеньев (точки О1 и О2) опустим на нормаль N-N перпендикуляры О1М1 и О2М2. Векторы 
и 
скоростей точки С, принадлежащей профилям П1 и П2, перпендикулярны отрезкам О1С и О2С и по модулю соответственно равны:
; 
.
Рис. 1.32. Схема передачи вращения двумя звеньями
Спроецируем векторы и на направление нормали N-N и касательной К-К. Учитывая геометрическое подобие треугольников О1М1С и Сu1uN1, а также треугольников О2М2С и Сu2uN2, получим:
|
|
|
; 
.
Если uN1 ¹ uN2, то профиль П1 либо должен проникнуть в профиль П2, либо отстать от него, что исключается. Из равенства этих составляющих:
w1 × О1М1 = w2 О2М2,
следует
.
Из подобия треугольников О1М1W и О2М2W:
.
Окончательно имеем
. (1.82)
Соотношение (1.82) выражает основной закон зацепления: общая нормаль N-N к профилям, проведенная в точке C их касания, делит межосевое расстояние аw на части, обратно пропорциональные угловым скоростям. При постоянном передаточном отношении ( 
= const) и зафиксированных центрах О1 и О2 точка W будет занимать на линии центров неизменное положение. При этом проекции скорости uk1 и uk2 не равны. Их разность указывает на относительное скольжение профилей в направлении касательной К-К, что вызывает их износ. Равенство проекций скоростей 
и 
возможно только в одном положении, когда точка С контакта профилей совпадет с точкой W пересечения нормали N-N и линии центров О1О2. Точка W называется полюсом зацепления, а окружности с диаметрами dw1 и dw2, которые касаются в полюсе зацепления и перекатываются друг по другу без скольжения, называются начальными.
Для обеспечения постоянства передаточного отношения теоретически один из профилей может быть выбран произвольно, но форма профиля сопряженного зуба должна быть строго определенной для выполнения условия (1.82). Наиболее технологичными в изготовлении и эксплуатации являются эвольвентные профили. Существуют и другие виды зацепления: циклоидальное, цевочное, зацепление Новикова, удовлетворяющие данному требованию.
|
|
|
