 |
21 (повышенный уровень, время – 6 мин)
|
|
|
|
21 (повышенный уровень, время – 6 мин)
Тема: Анализ программы с подпрограммами.
Что нужно знать:
· функция – это вспомогательный алгоритм, который возвращает некоторое значение–результат
· в Паскале функция располагается выше основной программы и оформляется следующим образом (вместо многоточия могут быть любые операторы):
function F(x: integer): integer;
begin
...
F: = < результат функции>
end;
· в заголовке функции записывают имя функции, в скобках – список параметров, далее через двоеточие – тип возвращаемого значения; в приведенном примере функция F принимает один целый параметр, к которому внутри функции нужно обращаться по имени x, и возвращает целое число
· результат функции записывается в специальную переменную, имя которой совпадает с именем функции; объявлять эту переменную не нужно
· если параметров несколько, для каждого из них указывают тип:
function F(x: integer; y: integer): integer;
· если несколько соседних параметров имеют одинаковый тип, можно их объединить в список:
function F(x, y: integer): integer;
· следующая программа ищет наименьшее значение функции F(x) на интервале [a, b], просматривая значения от a до b с шагом 1:
M: =a; R: =F(a);
for t: =a to b do
if F(t) < R then begin
R: =F(t); M: =t;
end;
· цикл для поиска наибольшего значения выглядит точно так же, только знак < нужно заменить на знак >
· если функция представляет собой квадратный трехчлен вида 
, то абсцисса, соответствующая точке минимума, вычисляется по формуле
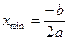
этот результат можно получить (вывести, если забыли), например, так:
§ в критической точке (точке минимума, точке максимума или точке перегиба) производная функции обращается в 0;
|
|
|
§ находим производную 
§ приравниваем ее к нулю: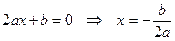 
.
· если квадратный трехчлен задан в виде 
, то абсцисса, соответствующая точке минимума, вычисляется по формуле
Пример задания:
P-17. Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
Var a, b, t, M, R: integer;
Function F(x: integer): integer;
begin
F: = abs( abs(x-5) + abs(x+5) - 3) + 12;
end;
BEGIN
a: =-20; b: =20;
M: =a; R: =F(a);
for t: =a to b do begin
if (F(t)< R)then begin
M: =t;
R: =F(t);
end;
end;
write(M+R);
END.
Решение:
1) заметим, что в программе есть цикл, в котором переменная t принимает последовательно все целые значения в интервале от a до b:
for t: =a to b do begin
...
end;
2) до начала цикла в переменную M записывается значение a, а в переменную R – значение функции в точке a:
M: =a; R: =F(a);
3) внутри цикла есть условный оператор, в котором вычисляется значение функции F(t) и сравнивается со значением переменной R:
if (F(t)< R)then begin
M: =t;
R: =F(t);
end;
если новое значение функции меньше, чем значение R, в R записывается значение функции в точке t, а в переменной M запоминается само значение t (аргумент функции, соответствующий значению в R)
4) в результате анализа пп. 1-3 можно сделать вывод, что цикл ищет минимум функции F(t) на интервале от a до b, и после выполнения цикла в переменной M оказывается значение аргумента t, при котором функция достигает минимума на заданном интервале (здесь это интервал [-20, 20])
5) запишем заданную функцию в привычном «математическом» виде:
f(x) = | | x – 5 | + | x + 5 | – 3 | + 12
чтобы найти минимум этой функции без ручного перебора всех целых значений x, нам нужно представлять, как идёт её график
6) сначала рассмотрим функцию под знаком «большого» модуля g(x) = | x – 5 | + | x + 5 | – 3;
|
|
|
7) находим нули выражений под знаком модуля и отмечаем их на числовой оси:
8) раскрываем модули отдельно для каждого интервала; рассматриваем интервал (–¥; –5), раскрываем модули (оба с обратным знаком):
g(x) = – (x – 5) – (x + 5) – 3 = – 2x – 3
на этом интервале функция убывает
9) 
рассматриваем полуинтервал [–5; 5), раскрываем модули:
g(x) = – (x – 5) + (x + 5) – 3 = 7
это значит, что на полуинтервале [–5; 5) функция принимает постоянное значение
10) рассматриваем полуинтервал [5; ¥ ), раскрываем модули:
g(x) = (x – 5) + (x + 5) – 3 = 2x – 3
на этом интервале функция возрастает
график функции показан на рисунке справа
11) как мы показали, на всей числовой оси функция g(x) принимает положительные значения, так что | g(x) | = g(x), поэтому f(x) = | g(x) | + 12 = g(x) + 12
12) во всех точках на отрезке [-5; 5] функции f(x) равно 7 + 12 = 19, поэтому программа найдёт одну из этих точек как точку минимума
13) осталось понять, какую именно точку она найдёт; посмотрим на программу: запоминание новой точки минимума происходит только тогда, когда только что вычисленное значение F(t) станет строго меньше, чем хранящееся в переменной R:
|
|
|
