 |
var a,b,t,M,R,H :integer;. Function F(H, x: integer):integer;. readln(H);. M := a; R := F(H, a);. for t := a to b do begin
|
|
|
|
var a, b, t, M, R, H: integer;
Function F(H, x: integer): integer;
begin
F: = 11*(x-H)*(x-H)+13;
end;
BEGIN
readln(H);
a: = -10; b: = 30;
M: = a; R: = F(H, a);
for t: = a to b do begin
if (F(H, t) > R) then begin
M: = t;
R: = F(H, t)
end
end;
write(R)
END.
Решение:
1) заметим, величина H в программе не изменяется, то есть фактически выполняет роль константы; она передаётся в функцию и влияет на значение функции
2) что в программе есть цикл, в котором переменная t принимает последовательно все целые значения в интервале от a до b:
for t: =a to b do begin
...
end;
3) до начала цикла в переменную M записывается значение a, а в переменную R – значение функции в точке a:
M: =a; R: =F(H, a);
4) внутри цикла есть условный оператор, в котором вычисляется значение функции F(t) и сравнивается со значением переменной R:
if (F(H, t) > R)then begin
M: =t;
R: =F(H, t)
end;
если новое значение функции больше, чем значение R, в R записывается значение функции в точке t, а в переменной M запоминается само значение t (аргумент функции, соответствующий значению в R)
5) в результате анализа пп. 1-3 можно сделать вывод, что цикл ищет максимум функции F(H, t) на интервале от a до b
6) заметим, что выводится значение R, а величина M не выводится и не влияет на вычисление R, поэтому можно не обращать на неё внимания
7) функция F вычисляет значение
F: =11*(x-H)*(x-H) + 13;
8) график этой эта функции – парабола с ветвями, направленными вверх (коэффициент при x2 = 11 > 0)
9) вершина параболы находится в точке x = H, ветви идут симметрично влево и вправо вверх
10) при изменении H парабола двигается влево или вправо (но не вверх-вниз! )
|
|
|
11) итак, мы ищем максимальное значение квадратичной функции, и хотим, чтобы это значение было наименьшим
12) давайте подвигаем параболу в пределах отрезка [a; b]:
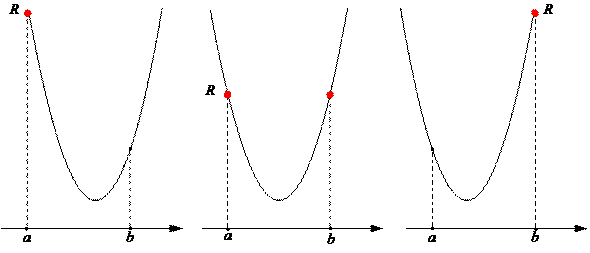
13) видно, что минимальное значение максимума будет тогда, когда вершина параболы будет расположена точно в середине отрезка [a; b]
14) отсюда требуемое значение H равно среднему арифметическому между a = –10 и b = 30:
H = (–10 + 30) / 2 = 10
15) Ответ: 10.
Ещё пример задания (И. Тощенко):
P-08. Напишите в ответе число различных значений входной переменной k, при которых программа выдаёт тот же ответ, что и при входном значении k = 35. Значение k = 35 также включается в подсчёт различных значений k.
var k, i: longint;
function F(x: longint): longint;
begin
F: =2*x*x+3*x+2
end;
begin
i: = 15;
readln(K);
while (i> 0) and (F(i) > K) do
i: =i-1;
writeln(i)
end.
Решение (И. Тощенко):
1) Вычислим значения функции F при i=1, 2, 3…
i=0: f(0)=2
i=1: f(1)=7
i=2: f(2)=16
i=3: f(3)=29
i=4: f(4)=46
2) Заданное значение К попадает в отрезок [29; 45].
3) Следовательно, всего 45-29+1=17 чисел.
4) ответ: 17.
Ещё пример задания:
P-07. Напишите в ответе число различных значений входной переменной k, при которых программа выдаёт тот же ответ, что и при входном значении k = 64. Значение k = 64 также включается в подсчёт различных значений k.
var k, i: longint;
function f(n: longint): longint;
begin
f: = n * n
end;
begin
readln(k);
i: = 12;
while (i> 0) and (f(i)> =k) do
i: = i-1;
writeln(i)
end.
Решение:
1) заметим, что функция F(x) вычисляет квадрат переданного ей числа
2) в теле основной программы выполняется цикл с условием, который заканчивается, когда значение функции станет меньше k
3) на каждом шаге цикла уменьшается значение переменной i, начиная с 12; цикл также заканчивается, когда значение переменной i станет равно 0
|
|
|
4) после окончания цикла программа выводит значение переменной i.
5) итак, функция выводит первое натуральное значение i, квадрат которого меньше, чем введённое с клавиатуры значение переменной k
6) при k = 64 программа выведет значение 7, поскольку это наибольшее натуральное число, квадрат которого меньше, чем 64
7) фактически нужно ответить на вопрос: сколько есть таких чисел k, которые меньше или равны 82 = 64 и больше, чем 72 = 49 (легко проверить, что при k=65 программа выведет значение 8, в при k=49 – значение 6)
8) в диапазоне [50; 64] всего 64-50+1=15 чисел, это и есть правильный ответ.
9) ответ: 15.
Ещё пример задания:
P-06. Определите, количество чисел K, для которых следующая программа выведет такой же результат, что и для K = 24:
var i, k: integer;
function F(x: integer): integer;
begin
F: =x*x*x;
end;
begin
i: = 12;
readln(K);
while (i> 0) and (F(i) > K) do
i: =i-1;
writeln(i);
end.
Решение:
1) заметим, что функция F(x) вычисляет куб переданного ей числа
2) перед началом цикла значение переменной i равно 12, в цикле оно уменьшается
3) цикл while останавливается, когда переменная i становится равна нулю или значение функции F(i) становится меньше или равно K
4) таким образом, в данной фактически требуется найти количество натуральных чисел в диапазоне [1.. 12], куб которых больше, чем K = 24
5) определим, у скольких чисел куб меньше, чем 24; это все числа, меньшие, чем 
, то есть, только числа 1 и 2; поэтому программа выведет 2 – первое число, куб которого меньше или равен 24
6) остаётся определить, когда программа выведет именно 2; это случится при всех K, при которых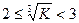 
, то есть при 
; в этот диапазон входит 27-8 = 19 чисел
7) Ответ: 19.
Ещё пример задания:
P-05. Определите, количество чисел K, для которых следующая программа выведет такой же результат, что и для K = 24:
|
|
|
