 |
function f(x: integer): integer;
|
|
|
|
function f(x: integer): integer;
begin
if x mod 2 =1 then
f: = x mod 10 + f(x div 10)
else
f: = 0;
end;
var N: integer;
begin
readln(n);
writeln(f(N));
end.
Решение:
1) В первую очередь необходимо разобраться, как работает описанная в программе функция. Заметим, что функция рекурсивная, (x div 10) – это число х без последней своей цифры, a (x mod 2) – остаток от деления х на 2, то есть признак делимости этого числа (и его младшей цифры) на 2.
2) Если на вход функции подается число, младшая цифра которого четная, то функция возвращает 0, иначе она возвращает сумму этой цифры и значения функции от аргумента без последней цифры. Если, например, подать на вход функции число, содержащее только нечетные цифры, она возвратит сумму эти цифр (при целочисленном делении на 10 старшей цифры получится 0, что завершит рекурсию). Таким образом, функция f возвращает сумму первой непрерывной последовательности нечетных цифр числа х, начиная с младшей.
3) Для входного числа 1133 значение функции равно 8. Это значение можно было получить и при ручном выполнении программы, но это не дало бы понимания работы функции.
4) Найдем в требуемом диапазоне числа, у которых сумма непрерывной последовательности нечетных цифр, начиная с младшей, равна 8. Сумма состоит не более, чем из четырех слагаемых. Покажем, что при разложении числа 8 на нечетные слагаемые могут возникнуть суммы только из двух или четырех цифр: действительно, если сложить три нечетных числа, то и сумма будет нечетной, а единственное нечетное число не может быть равным 8.
5) Сначала найдем разложение числа 8 на сумму четырех нечетных цифр: 8=1+1+3+3. Количество чисел, состоящих из этих цифр, равно 6. Другое разложение: 8=5+1+1+1; количество чисел, составленных из этих цифр, равно 4.
|
|
|
6) Теперь найдем разложения числа 8 на два нечетных слагаемых: 8=5+3 и 8=7+1. Старшая цифра в искомых числах может принимать 9 значений (от 1 до 9), вторая цифра – любое четное значение (5 штук). Таким образом, количество чисел с последовательностью нечетных цифр, начиная с младшей, длиной 2 и суммой 8 есть 9*5*2*2=180.
7) Ответ: 190.
Ещё пример задания:
P-11. Напишите в ответе наименьшее значение входной переменной k, при котором программа выдаёт тот же ответ, что и при входном значении k = 10.
var k, i: longint;
function f(n: longint): longint;
begin
f: = n * n * n;
end;
function g(n: longint): longint;
begin
g: = 2*n + 3;
end;
begin
readln(k);
i: = 1;
while f(i) < g(k) do
i: = i+1;
writeln(i)
end.
Решение:
1) сначала заметим, что функция f возвращает куб переданного ей числа, а функция g – результат вычисления 2*n+3
2) при некотором i работа цикла останавливается: это происходит при нарушении условия
f(i)< g(k), то есть при выполнении обратного условия f(i)³ g(k)
3) в то же время на предыдущем шаге цикла (для i-1) условие его работы выполнялось, то есть
f(i-1)< g(k), откуда получаем
f(i-1)< g(k)£ f(i)
4) вспоминая, что f(i)=i3, делаем вывод, что g(k) должно быть между кубами двух соседних чисел: (i-1)3 < g(k) £ i3
5) для заданного k=10 находим g(10)=2·10+3=23, так что i=3:
(2)3 < g(k)=23 £ 33
6) осталось проверить, при каких k выполняется условие
8 < g(k)=2k+3 £ 27
7) решая двойное неравенство относительно k получаем
2, 5 < k £ 12
8) таким образом, минимальное целое число, соответствующее условию – 3.
9) Ответ: 3.
Ещё пример задания:
P-10. Напишите в ответе число, равное количеству различных значений входной
переменной k, при которых приведённая ниже программа выводит тот же
ответ, что и при входном значении k = 10. Значение k = 10 также включается
|
|
|
в подсчёт различных значений k.
var k, i: longint;
function f(n: longint): longint;
begin
f: = n * n * n;
end;
begin
readln(k);
i: = 1;
while f(i) < k do
i: = i+1;
if f(i)-k < = k-f(i-1) then
writeln(i)
else writeln(i-1);
end.
Решение:
1) сначала заметим, что функция f возвращает куб переданного ей числа
2) после ввода k работает цикл, который увеличивает i до тех пор, пока значение куба f(i) не станет больше или равно k – тогда нарушится условие f(i)< k и цикл завершится
3) построим таблицу значений функции f(i) (кубов чисел):
| i | f(i) | Цикл завершается для … |
| k=1 | ||
| k=2,..., 8 | ||
| k=9,..., 27 |
4) таким образом, при k=10 цикл завершится при i=3
5) главная «новинка» – в условном операторе
if f(i)-k < = k-f(i-1) then
writeln(i)
else writeln(i-1);
6) например, при k=10 и i=3 условие
f(i)-k < = k-f(i-1)
27-10 < = 10-8
17 < = 2
неверно, из-за этого выводится на экран не i, а i-1, то есть 2
7) итак, нам нужно найти, сколько значений k дадут на выходе 2
8) посмотрим внимательно на условие в условном операторе, преобразуем его к виду
f(i)+f(i-1) < = 2k
9) тогда при выполнении обратного условия,
2k < f(i)+f(i-1)
k < (f(i)+f(i-1))/2
выводится число i-1 вместо i
10) составим еще одну таблицу:
| i | (f(i)+f(i-1))/2 | Выводится i-1 для … | Выводится i для … |
| 4, 5 | k=2,..., 4 | k=5,..., 8 | |
| 17, 5 | k=9,..., 17 | k=18,..., 27 |
11) таким образом, в этой задаче нам подходят числа в диапазоне [5; 17], всего их 17-5+1 = 13
12) Ответ: 13.
Решение (вариант 2, Д. Муфаззалов, Уфа):
1) Сначала определим, какое число выводит программа при входном значении k = 10. Для этого определим, чему равно значение переменной i после выхода из цикла. Из принципа работы цикла while получим систему неравенств:

Решим ее в натуральных числах (по программе i увеличивается в цикле на 1, начиная с 1 ):
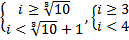 ,
,  =3.
=3.
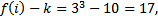

17> 2, логическое выражение в операторе if ложно, поэтому программа выводит на экран число 2.
2) Чтобы программа выводила число 2, после выхода цикла значение переменной i должно быть равно 2 или 3, при этом должны выполняться соответствующие условия из оператора if.
3) Рассмотрим случай, когда после выхода цикла значение переменной i равно 2. Тогда имеет место следующая система неравенств:
|
|
|
 .
.
Решая ее в целых числах (по программе k – целое), получим:
 .
.
Целых чисел, удовлетворяющих этой системе, 4.
4) Рассмотрим случай, когда после выхода цикла значение переменной i равно 3. Тогда имеет место следующая система неравенств:
 .
.
Решая ее в целых числах, получим:
 .
.
Целых чисел, удовлетворяющих этой системе, 9.
5) Так как полученные множества не пересекаются, получаем ответ 4+9=13
6) Ответ: 13.
Ещё пример задания:
P-09. Определите, какое значение H нужно ввести, чтобы число, напечатанное в результате выполнения следующего алгоритма, было наименьшим.
|
|
|


