 |
var k, i : longint;. function f(n: longint) : longint;. readln(k);. while f(i) < k do. if f(i)-k <= k-f(i-1) then. writeln(i)
|
|
|
|
var k, i: longint;
function f(n: longint): longint;
begin
f: = n * n * n;
end;
begin
readln(k);
i: = 1;
while f(i) < k do
i: = i+1;
if f(i)-k < = k-f(i-1) then
writeln(i)
else writeln(i-1)
end.
Решение (И. Щеголяева):
1) Определяем, что будет напечатано при 
.
| i | ||||
| f(i) | ||||
| f(i) < k | + | + | – | |
| f(i) – k £ k – f(i-1) | 27-25 £ 25-8, верно | |||
| Вывод на экран |
2) Следовательно, последнее значение переменной i может быть равно 3, если условие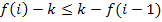 
истинно или может быть равно 4, если условие ложно. Т. е. при i=3 должно выполняться условие 
при i = 4 должно выполняться условие 
3) Найдем левую границу. Преобразуем первое выражение:
Поскольку значение k должно быть целым, то k ³ 18.
4) Найдем правую границу. Преобразуем второе выражение:
Поскольку значение k должно быть целым, то k £ 45.
5) Таким образом, 
, т. е всего 28 различный значений.
6) Ответ: 28.
Ещё пример задания (Д. Муфаззалов, Белград):
P-14. Напишите в ответе количество различных значений входной переменной a из интервала от 1 до 100 (включая границы), при которых программа выдаёт тот же ответ, что и при входном значении a = 20. Значение a = 20 также включается в подсчёт различных значений a.
var i, k, a: integer;
function f(x: integer): integer;
begin
if x > 1 then
f: = x mod 2 * f(x div 2)
else
f: = x;
end;
begin
k: = 0;
readln(a);
for i: = 1 to a do
if f(i) =1 then k: =k+1;
writeln(k);
end.
Решение:
1) Рассмотрим, как работает функция, приведенная в программе. Заметим, что (x mod 2) – младшая цифра двоичного представления числа х в двоичной системе счисления, (x div 2) – число х без младшей своей цифры в двоичном представлении.
|
|
|
2) Таким образом, функция находит произведение цифр числа в двоичном представлении. Программа в целом находит количество чисел, произведение цифр в двоичной записи которых равно 1, то есть таких чисел, двоичная запись которых не содержит нулей.
3) В общем виде такие числа можно представить, как 2n-1, где n – натуральное число. В диапазоне от 1 до 20 таких чисел 4: 1, 3, 7, 15. А в диапазоне от 1 до 100 – 6: 1, 3, 7, 15, 31, 63.
4) Таким образом, искомые числа – это числа от 15 до 30.
5) Ответ: 16.
Ещё пример задания (Д. Муфаззалов, Белград):
P-13. Какое число будет напечатано в результате выполнения программы?
var i, k: integer;
function f(x: integer): integer;
begin
if x > 0 then
f: = x mod 2 + f(x div 2)
else
f: = 0;
end;
begin
k: = 0;
for i: = 0 to 1023 do
if f(i mod 32) = 1 then
if f(i div 32) = f(i mod 32) then k: = k + 1;
writeln(k);
end.
Решение:
1) Рассмотрим, как работает функция, приведенная в программе. Заметим, что (x mod 2) – младшая цифра двоичного представления числа х в двоичной системе счисления, (x div 2) – число х без младшей своей цифры в двоичном представлении, (i mod 32) - число, составленное из пяти младших битов двоичной записи числа i, (i div 32) – число, составленное из пяти старших битов двоичной записи числа i. Таким образом, функция считает сумму цифр двоичной записи аргумента.
2) В основной части программы рассматриваются числа от 1 до 1023, счетчик увеличивается на 1, если сумма цифр в младших пяти разрядах двоичного представления числа равна 1, и сумма цифр в старших пяти разрядах двоичного представления числа тоже равна 1.
3) Таким образом, необходимо найти количество чисел, в двоичной записи которых в младших пяти разрядах и в старших пяти разрядах находится ровно по одной единице.
|
|
|
4) Дополняя двоичное представление чисел до 10 битов, получим, что старшая единица может располагаться на 5 позициях; в каждом таком случае младшая единица может тоже располагаться на пяти позициях. Тогда количество таких чисел равно 5*5=25.
5) Ответ: 25.
Ещё пример задания (Д. Муфаззалов, Белград):
P-12. Сколько существует таких четырехзначных натуральных чисел, что при вводе их программа выведет такое же число, что и при вводе числа 1133. Значение 1133 также включается в подсчёт.
|
|
|
