Количественные методы принятия финансовых решений

Расчет суммы простого процента в процессе наращения стоимости (компаундинг):

,(1)

где I – сумма процента за обусловленный период времени в целом;

PV – первоначальная сумма (стоимость) денежных средств;

n – количество интервалов, по которым осуществляется расчет

процентных платежей, в общем обусловленном периоде времени;

i – используемая процентная ставка, выраженная десятичной

дробью.

В этом случае будущая стоимость вклада (FV) с учетом начисленной суммы процента определится по формуле

. (2)

Множитель называется множителем (или коэффициентом) наращения суммы простых процентов. Его значение всегда должно быть больше 1.

Расчет суммы простого процента в процессе дисконтирования стоимости (т.е. суммы дисконта) используется следующая формула:

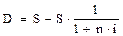,(3)

где D – сумма дисконта (рассчитанная по простым процентам)

за обусловленный период времени в целом;

S – стоимость денежных средств;

n – количество интервалов, по которым осуществляется расчет

процентных платежей, в общем обусловленном периоде времени;

i – используемая дисконтная ставка, выраженная десятичной

дробью.

Вэтом случае настоящая стоимость денежных средств (РV) с учетом рассчитанной суммы дисконта определится по следующей формуле:

. (4)

Используемый множитель 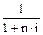называется дисконтным множителем (коэффициентом) суммы простых процентов, значение которого всегда должно быть меньше 1.

Расчет будущей стоимости вклада (стоимости денежных средств) в процессе его наращения по сложным процентам используется следующая формула:

, (5)

где S_c – будущая стоимость вклада (денежных средств) при его

наращении по сложным процентам;

PV – первоначальная сумма вклада;

i – используемая процентная ставка, выраженная десятичной

дробью;

n – количество интервалов, по которым осуществляется каждый

процентный платеж, в общем обусловленном периоде времени.

Расчет настоящей стоимости денежных средств в процессе дисконтирования по сложным процентам производится:

,(6)

где Р_с – первоначальная сумма вклада;

S – будущая стоимость вклада при его наращении, обусловленная

условиями инвестирования;

i – используемая дисконтная ставка, выраженная десятичной

дробью;

n – количество интервалов, по которым осуществляется каждый

процентный платеж, в общем обусловленном периоде времени.

Расчет будущей стоимости аннуитета на условиях предварительных платежей (пренумерандо) используется следующая формула:

, (7)

где S_Apre – будущая стоимость аннуитета, осуществляемого

на условиях предварительных платежей (пренумерандо);

R – характеризует размер отдельного платежа;

i – используемая процентная ставка, выраженная десятичной

дробью;

n – количество интервалов, по которым осуществляется каждый

процентный платеж, в общем обусловленном периоде времени.

Расчет будущей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо) используется формула

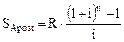, (8)

где S_Apost – будущая стоимость аннуитета, осуществляемого

на условиях последующих платежей (постнумерандо);

R – характеризует размер отдельного платежа;

i – используемая процентная ставка, выраженная десятичной

дробью;

n – количество интервалов, по которым осуществляется каждый

процентный платеж, в общем обусловленном периоде времени.

Расчет настоящей стоимости аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо) используется следующая формула:

,(9)

где Р_Apre – настоящая стоимость аннуитета, осуществляемого

на условиях предварительных платежей (пренумерандо);

R – характеризует размер отдельного платежа;

i – используемая процентная (дисконтная) ставка, выраженная

десятичной дробью;

n – количество интервалов, по которым осуществляется каждый

процентный платеж, в общем обусловленном периоде времени.

Расчет настоящей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо):

,(10)

где Р_Apost – настоящая стоимость аннуитета, осуществляемого

на условиях последующих платежей (постнумерандо);

R – характеризует размер отдельного платежа;

i – используемая процентная (дисконтная) ставка, выраженная

десятичной дробью;

n – количество интервалов, по которым осуществляется каждый

процентный платеж, в общем обусловленном периоде времени.

При оценке будущей стоимости денежных средств с учетом фактора инфляции используется следующая формула:

,(11)

где S_н – номинальная будущая стоимость вклада (денежных

средств), учитывающая фактор инфляции;

РV – первоначальная сумма вклада;

I_p – реальная процентная ставка, выраженная десятичной

дробью;

ТИ – прогнозируемый темп инфляции, выраженный десятичной

дробью;

n – количество интервалов, по которым осуществляется каждый

процентный платеж, в общем обусловленном периоде времени.

При оценке будущей стоимости денежных средств с учетом фактора инфляции используется следующая формула:

,(12)

где S_н – номинальная будущая стоимость вклада (денежных средств),

учитывающая фактор инфляции;

РV – первоначальная сумма вклада;

I_p – реальная процентная ставка, выраженная десятичной дробью;

ТИ – прогнозируемый темп инфляции, выраженный десятичной

дробью;

n – количество интервалов, по которым осуществляется каждый

процентный платеж, в общем обусловленном периоде времени.

При оценке настоящей стоимости денежных средств с учетом фактора инфляции используется формула

,(13)

где Р_р – реальная настоящая сумма вклада (денежных средств),

учитывающая фактор инфляции;

S_н – ожидаемая номинальная будущая стоимость вклада

(денежных средств);

I_p – реальная процентная ставка, используемая в процессе

дисконтирования стоимости, выраженная десятичной дробью;

ТИ – прогнозируемый темп инфляции, выраженный десятичной

дробью;

n – количество интервалов, по которым осуществляется каждый

процентный платеж, в общем обусловленном периоде времени.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: