Определение достоверности различий по t-критерию Стьюдента

/-Критерий Стьюдента относится к параметрическим, следо­вательно, его использование возможно только в том случае, ког­да результаты эксперимента представлены в виде измерений по двум последним шкалам — интервальной и отношений [5, 6, 7]. Проиллюстрируем возможности критерия Стьюдента на конкрет­ном примере.

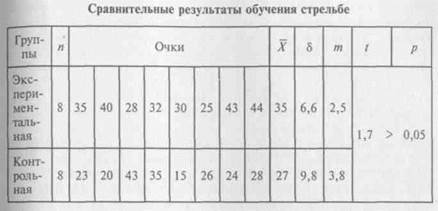
Предположим, вам необходимо выяснить эффективность обу­чения стрельбе по определенной методике. С этой целью прово­дится сравнительный педагогический эксперимент, где одна группа (экспериментальная), состоящая из 8 человек, занимается по предлагаемой экспериментальной методике, а другая (контроль­ная) — по традиционной, общепринятой. Рабочая гипотеза зак­лючается в том, что новая, предлагаемая вами методика окажется более эффективной. Итогом эксперимента является контрольная стрельба из пяти выстрелов, по результатам которых (табл. 6) нужно рассчитать достоверность различий и проверить правильность выд­винутой гипотезы.

Таблица 6

Что же необходимо сделать для расчета достоверности разли­чий по /-критерию Стьюдента?

1. Вычислить средние арифметические величины X для каждой
группы в отдельности по следующей формуле:

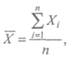
где X_t — значение отдельного измерения; я — общее число изме­рений в группе.

Проставив в формулу фактические значения из табл. 6, получим:

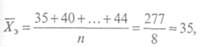
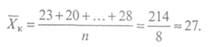
Сопоставление среднеарифметических величин доказывает, что в экспериментально^ группе данная величина (X, = 35) выше, чем в контрольной (Х_к = 27). Однако для окончательного утверж­дения того, что занимающиеся экспериментальной группы на­учились стрелять лучше, следует убедиться в статистической дос­товерности различий (/) между рассчитанными среднеарифмети­ческими значениями.

2. В обеих группах вычислить стандартное отклонение (5) по
следующей формуле:

:де X_imax — наибольший показатель; X_imm — наименьший показа­тель; К — табличный коэффициент. Порядок вычисления стандартного отклонения (5): — определить X_itrax в обеих группах; — определить X_imia в этих группах; — определить число измерений в каждой группе (л); — найти по специальной таблице (приложение 12) значение коэффициента К, который соответствует числу измерений в группе (8). Для этого в левом крайнем столбце под индексом (и) находим цифру 0, так как количество измерений в нашем примере меньше 10, а в верхней строке — цифру 8; на пересечении этих строк — 2,85, что соответствует значению коэффициента.АГпри 8 испыту-— подставить полученные значения в формулу и произвести необходимые вычисления:

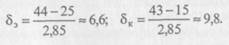
3. Вычислить стандартную ошибку среднего арифметического
значения (т) по формуле:

Для нашего примера подходит первая формула, так как п < 30. Вычислим для каждой группы значения:

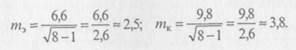
4. Вычислить среднюю ошибку разности по формуле:

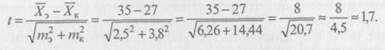
т

5. По специальной таблице (приложение 13) определить досто­
верность различий. Для этого полученное значение (t) сравнивает­
ся с граничным при 5 %-ном уровне значимости (t_0fi5) ^ПР^И числе
степеней свободы/= п_э + п_к - 2, где п_эк п_к~ общее число инди­
видуальных результатов соответственно в экспериментальной и
контрольной группах. Если окажется, что полученное в экспери­
менте t больше граничного значения (/₀₎о5)> ^т0 различия между
средними арифметическими двух групп считаются достоверными
при 50 %-ном уровне значимости, и наоборот, в случае когда
полученное t меньше граничного значения t_0<05, считается, что раз­
личия недостоверны и разница в среднеарифметических показате­
лях групп имеет случайный характер. Граничное значение при 5 %-
ном уровне значимости (Г_0>05) определяется следующим образом:

— вычислить число степеней свободы/= 8 + 8 - 2 = 14;

— найти по таблице (приложение 13) граничное значение t_ofi5 при/= 14.

В нашем примере табличное значение t_Q<05 = 2,15, сравним его с вычисленным Г, которое равно 1,7, т.е. меньше граничного значения (2,15). Следовательно, различия между полученными в эксперименте средними арифметическими значениями считаются недостоверными, а значит, недостаточно оснований для того, чтобы говорить о том, что одна методика обучения стрельбе ока­залась эффективнее другой. В этом случае можно записать: / = 1,7 при/» > 0,05, это означает, что в случае проведения 100 аналогич-

ньгх экспериментов вероятность (р) получения подобных резуль­татов, когда средние арифметические величины эксперименталь­ных групп окажутся выше контрольных, больше 5 %-ного уров­ня значимости или меньше 95 случаев из 100. Итоговое оформле­ние таблицы с учетом полученных расчетов и с приведением соответствующих параметров может выглядеть следующим обра­зом (табл. 7).

Таблица 7

При сравнительно больших числах измерений условно приня­то считать, что если разница между средними арифметическими показателями равна или больше трех своих ошибок, различия счи­таются достоверными. В этом случае достоверность различий опре­деляется по следующему уравнению:

Как уже говорилось в начале этого раздела, /-критерий Стью-дента может применяться только в тех случаях, когда измерения сделаны по шкале интервалов и отношений. Однако в педагоги­ческих исследованиях нередко возникает потребность определять Достоверность различий между результатами, полученными по Шкале наименований или порядка. В таких случаях используются непараметрические критерии. В отличие от параметрических не­параметрические критерии не требуют вычисления определен­ных параметров полученных результатов (среднего арифметичес­кого, стандартного отклонения и т.п.), чем в основном и связа­ны их названия. Рассмотрим сейчас два непараметрических крите­рия для определения достоверности различий между независимы­ми результатами, полученными по шкале порядка и наименова­ний.

 

 

 

 

выбора критериев при зависимых (сопряженных, связанных) и независимых результатах можно воспользоваться таблицей (при­ложение 11).

Наряду с относительно простыми способами сравнения одной выборки с другой в исследовательской работе встречаются и бо­лее сложные задачи, когда приходится сравнивать одновременно несколько выборок, объединяемых в единый статистический ком­плекс. В этих случаях используется дисперсионный анализ.

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: