 |
Решение игры в чистых стратегиях
|
|
|
|
Пусть дана матрица игры (игра в нормальной записи):
где A и B – участники игры. Участник A выбирает стратегию.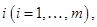 
а участник B выбирает стратегию 
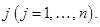Стратегии выбираются участниками независимо друг от друга. Выбору соответствует исход 
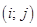с платежом 
. Он равен сумме выигрыша, который получает участника A и сумме проигрыша, который платит частник B. Естественным образом возникает вопрос: как найти лучшую стратегию для игрока A и для игрока B?
Понятие наилучшего (оптимального) решения является сложным понятием. Для того, чтобы утверждать, что какое-то решение является оптимальным, нужно знать, что именно мы понимаем под словом «оптимальный». Например, фирма, при выборе своих управленческих решений, может руководствоваться следующими соображениями:
§ максимизация прибыли;
§ минимизация издержек;
§ завоевать место на рынке;
§ стремиться к минимизации хозяйственных рисков;
§ и др.
Каждое из этих соображений приводит к определенному критерию оптимальности. Решения, которые оптимальны с точки зрения одного критерия, могут быть неоптимальными с точки зрения другого. Например, если фирма выбрала в качестве критерия оптимальности принцип достижения наибольшей прибыли, то может оказаться, что решение, которое обеспечивает наибольшую прибыль, приводит к появлению высоких хозяйственных рисков.
Одним из критериев оптимальности является критерий гарантированного результата. Этот критерий заключается в том, что наилучшим решением (оптимальной стратегией) будет такое решение, которое даёт игроку определённый (гарантированный) выигрыш (или проигрыш) независимо от действий других участников игры.
В соответствии с критерием гарантированного результата игрок A для каждой своей стратегии 
находит наихудший для себя, а значит наилучший для соперника исход, т.е. игрок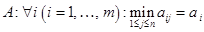 
. Следовательно 
– столбец самых плохих результатов. Далее игрок A выбирает такое значение i, которое соответствует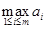 
. Иными словами, игрок A решает задачу 
или задачу максимина.
|
|
|
Игрок B для каждой стратегии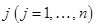 
находит наихудший результат, т.е. находит 
Следовательно получает строку 
Далее игрок B решает задачу нахождения минимума 
. Другими словами, игрок B решает задачу нахождения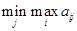 
или задачу минимакса.
Значение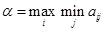 
называется нижним значением игры (нижняя цена игры); значение 
называется верхним значением игры (верхняя цена игры).
Теорема 1. Для любой матричной игры выполняется неравенство
(1.2)
То есть нижняя цена игры не больше чем верхняя цена игры.
Доказательство.
Зафиксируем значение i=1,2…,m и найдем наименьший элемент строки {ai1, ai2, …, ain}, который обозначим ail(i). Таким образом
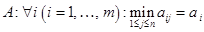l(i) (1.3)
Обозначим akl(k) наибольшее из чисел {a1l(1), a2l(2),…, aml(m)}, тогда
akl(k)= (1.4)
Зафиксируем значение j=1,2…,n и найдем наибольший элемент столбца {a1j, a2j, …, amj}, который обозначим ap(j)j. Таким образом
ap(j)j = (1.5)
Обозначим ap(q)q наименьшее из чисел { ap(1)1, ap(2)2,…, ap(n)n }, тогда
ap(q)q = 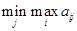(1.6)
Из (1.3) следует неравенство ail(i)≤aij, верное для всех i=1.2….,m и j=1.2…,n. Подставляя в него i=k, получим неравенство
α=akl(k)≤akj (1.7)
Из (1.5) следует неравенство ap(j)j≥aij, верное для всех i=1.2….,m и j=1.2…,n. Подставляя в него i=k, получим неравенство ap(j)j≥akj. Итак получаем
α=akl(k)≤akj≤ ap(j)j≤ ap(q)q=β, что и требовалось доказать.
Если первый игрок стремится получить гарантированный результат, то он выбирает из своего множества стратегий стратегию k, для которой наименьшее значение выигрыша равно нижнему значению игры α. Тогда при любом выборе вторым игроком стратегии j будет верно неравенство aij≥ α, то есть α является гарантированным выигрышем первого игрока.
|
|
|
Аналогично, если второй игрок стремится получит гарантированный результат, то он выберет стратегию q, для которой наибольшее значение проигрыша будет равно верхнему значению игры β. Тогда при любом выборе первым игроком стратегии i будет верно неравенство aij≤β, то есть β является гарантированным верхним значением проигрыша второго игрока.
Будет ли исход игры, реализующийся при стратегиях k и q, равновесным зависит от того, равны или нет числа α и β.
Если верхняя цена равна нижней цены игры, т.е. выполняется равенство:
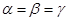(1.8)
то число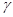 
называется чистой ценой игры.
Пусть платёжная матрица удовлетворяет уравнению (1.8). Это значит, что существует её элемент alk, для которого верно равенство
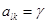(1.9)
Исход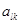 
достигается, когда игрок A выбирает стратегию l, а игрок B – стратегию k. В этом случае стратегия k называется оптимальной минимаксной стратегией игрока B, а элемент 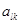называется седловой точкой (седлом) платёжной матрицы. Совокупность 
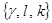(цена игры оптимальной стратегии) называется решением игры в чистых стратегиях.
Теорема 2. Если один участник игры выбирает свою оптимальную (максиминную/минимаксную) стратегию, то лучшим выбором для другого участника будет своя (минимаксная/максиминная) стратегия.
Доказательство. Пусть игрок A выбрал свою оптимальную стратегию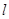 
, тогда для любых стратегий 
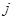игрока B будет справедливо неравенство 
. Для оптимальной стратегии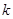 
игрока B будет выполняться неравенство 
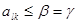, следовательно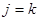 для 
, а для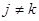 
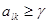. Из этого следует, что наилучшей стратегией для игрока B будет стратегия 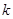. Аналогично доказывается обратная зависимость.
Итак, если платёжная матрица имеет седловую точку, то ни одному участнику игры не выгодно в одностороннем порядке отказываться от своей оптимальной (максиминной/минимаксной) стратегии. Другими словами в cедловой точке наблюдается баланс интересов, поэтому эту точку называют точкой равновесия.
Если платёжная матрица имеет седловую точку, то:
1) Игрок A имеет оптимальную максиминную стратегию;
2) Игрок B имеет минимаксную стратегию;
3) Применение оптимальных стратегий даёт ситуацию равновесия, которая оказывается равновесием в чистых стратегиях.
4) Игра имеет решени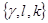е 
, где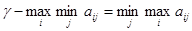 
. 
- оптимальные стратегии. .
|
|
|
Пример. Найти решение игры.
| B | ||||||||
| A | -22 | -7 | -8 | -22 | ||||
| -9 | -13 | -13 | ||||||
| -5 | -3 | -5 | ||||||
Решение. Игрок A руководствуясь принципом гарантированного результата. Для этого он в каждой строке ищет минимальный элемент, затем максимальное значение в полученном столбце минимумов
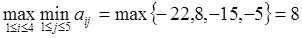
Игрок B:
.
- решение в чистых стратегиях предопределяющее исход игры для различных игроков.
Если верхняя и нижняя цены игры принимают различные значения, то согласно теореме 1 справедливо строгое неравенство α<β. В этом случае применение первым игроком максиминной стратегии дает возможность второму игроку сделать свой проигрыш меньшим, чем число β, если он откажется от минимаксной стратегии. И наоборот, применение вторым игроком минимаксной стратегии дает возможность первому игроку сделать выигрыш большим, чем число α, если он откажется от максиминной стратегии. Тогда исход, который реализуется при максиминной и минимаксной стратегиях, не будет равновесным. Других равновесных исходов также не существует, следовательно игра без седловой точки не имеет решения в чистых стратегиях.
Пример. Найти решение игры.
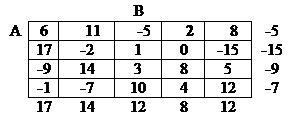
Решение. 
Чистой цены не существует. Равновесия в чистых стратегиях нет.
Пример. В платёжной матрице найти точку равновесия.
Точкой равновесия будет являться точка 6.
Пример. Посёлок Паново состоит из одной улицы. Два предпринимателя решили разместить свои киоски с продовольственными товарами. Других продовольственных магазинов в посёлке нет. Будем считать, что:
1. Оба киоска продают один и тот же ассортимент товаров по одним и тем же ценам;
2. Плотность жителей равномерно распределена по длине улицы.
Найти положение киосков, исходя из того, что каждый предприниматель стремится к наибольшей выручке.
Решение. Возьмём длину улицы за 1, тогда весь посёлок расположится на отрезке 
(Рис.1)
Рисунок 1
|
|
|
Обозначим x – координата первого киоска; y – координата второго киоска. Очевидно, что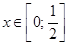 
Найдём выручку X первого киоска. Цену товара возьмём за 1.
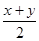– середина расстояния между x и y.
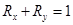
Первый предприниматель решает задачу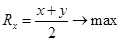 
,
а второй соответственно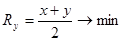 
.
Таким образом, получаем игру с постоянной суммой, равной 1.
Применим принцип гарантированного результата. Первый предприниматель ожидает, что второй будет выбирать такое значение y, чтобы выручка первого была минимальной, то есть он исходит из пессимистических ожиданий: 
1-й выбирает такой x, чтобы: 
2-й выбирает такой y, чтобы: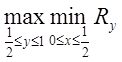 
Найдём оптимальные стратегии:
Аналогично
Таким образом, лучшими стратегиями будет размещение киосков на середине улицы спиной друг к другу. Это равновесие не выгодно жителям посёлка, но обеспечивает равновесие между предпринимателями.
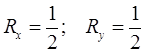
В примере два конкурента фактически борются за долю, превышающую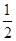 
, т.е. за выигрыш
,
где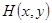 
– функция платежа,
если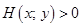 
– выигрыш x 
– выигрыш y.
Равновесие: 
.
Смешанное расширение игры
Пусть матричная игра представлена платежной матрицей с элементами aij, где i=1,2,…,m – стратегии первого игрока, j=1,2,…,n – стратегии второго игрока. Данные стратегии игроков будем называть чистыми стратегиями.
В предыдущем параграфе мы доказали, что решение матричной игры в чистых стратегиях (т.е. при выборе каждым игроком одной и только одной стратегии из заданного множества его стратегий) существует тогда и только тогда, когда платежная матрица имеет седловую точку. Рассмотрим выбор стратегий в игре без седловой точки. Если игрок может предвидеть, какую из чистых стратегий изберёт противник, он может найти наилучший ответ на ход противника. Таким образом, каждый игрок заинтересован в том, чтобы его ходы были непредсказуемы. Для этого необходимо ввести в выбор стратегий элемент случайности. Однако отсутствие логики при выборе стратегий ухудшит положение каждого из игроков. Компромисс заключается в том, что игроки чередуют (смешивают) свои стратегии случайным образом, но по определённой разумной схеме. Этой схеме должна соответствовать комбинация чистых стратегий.
Введем следующие изменения правил игры: каждый игрок наряду с отдельными стратегиями из своего множества стратегий может применять их комбинации, в которых стратегии представлены в определенных пропорциях.
Рассмотрим матричную игру, представленную Таблицей 5.
Таблица 5
| 2-й игрок | |
 
| |
| 1-й игрок |
где 
– частота (вероятность) с которой первый игрок собирается использовать свою стратегию 1;
– частота (вероятность) с которой первый игрок собирается использовать свою стратегию 2;
|
|
|
– частота (вероятность) с которой первый игрок собирается использовать свою стратегию m.
Вектор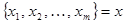 
называют смешанной стратегией первого игрока. Из определения вероятности:
.
Аналогично второй игрок чередует (смешивает) свои стратегии так, чтобы:
Стратегия 1 имела частоту (вероятность)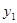 
;
Стратегия 2 имела частоту (вероятность) 
;
Стратегия n имела частоту (вероятность) 
.
Вектор 
называется смешанной стратегией второго игрока. Очевидно, что
.
Возможность применять наряду со стратегиям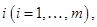и и 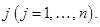, которые мы будем называть чистыми стратегиями 1-го и 2-го игроков соответственно, смешанных стратегий x и y, изменяет условия игры, расширяет их. Поэтому переход от чистых стратегий к смешанным стратегиям называют смешанным расширением игры.
Множества смешанных стратегий 1-го и 2-го игроков представляют собой соответственно:
– множество m -мерных векторов, координаты которых удовлетворяют условиям:
;
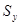– множество n -мерных векторов, координаты которых удовлетворяют условиям:
.
Очевидно, что чистые стратегии игроков входят как элементы в множество их смешанных стратегий.
Пусть первый игрок выбрал некоторую смешанную стратегию x, а второй – y. Тогда каждый исход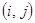 
из платёжной матрицы становится случайным событием. Найдём вероятность этого события. Для того, чтобы осуществился исход 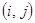, первый игрок выбирает стратегию i с вероятностью 
, а второй игрок выбирает стратегию j с вероятностью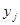 
. В силу независимости выбора вероятность исхода 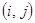равна вероятности совместных наступлений двух независимых событий, т.е. произведению их вероятностей .
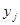Для каждой пары смешанных стратегий x€X и y€Y можно найти среднее значение выигрыша, которое мы обозначим 
. Это среднее значение будет равно математическому ожиданию платежа. Поскольку платёж 
осуществляется с вероятностью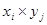 
, то математическое ожидание определяется по формуле
Легко проверить, что функция H(x,y) двух векторных переменных x и y будет непрерывна на компактном множестве Sx х Sy.
Очевидно, что первый игрок заинтересован в том, чтобы платёж 
был как можно больше, а второй в том, чтобы платёж был как можно меньше. В соответствии с принципом гарантированного результата 1-й игрок для каждой смешанной стратегии x из множества Sx определяет наименьшее по y значение функции H(x,y) на множестве Sy. Наименьшее значение, которое мы обозначим H (x,y(x)) существует и достигается при y=y(x) в силу непрерывности функции H(x,y) на компактном ограниченном множестве Sy. Так же можно доказать, что функция y=y(x) является непрерывной по x на компактном множестве Sx. Затем 1-й игрок находит значение векторного аргумента x*, для которого функция H(x,y(x)) достигает максимума на множестве Sx. В силу непрерывности функции H(x,y(x)) на компактном ограниченном множестве Sx, она достигает там своего наибольшего значения
Число 
называется нижним значением игры в смешанных стратегиях. Число 
называется верхним значением игры в смешанных стратегиях.
Теорема 3. Нижнее значение игры в смешанных стратегиях меньше или равно верхнему значению игры в смешанных стратегиях, т.е. справедливо неравенство
.
Доказательство
Зафиксируем смешанную стратегию x из множества Sx и обозначим H(x,y(x)) наименьшее значение функции H(x,y) на компактном ограниченном множестве Sy. Тогда для всех x из Sx и y из Sy выполняется неравенство
H(x,y(x))≤ H(x,y) (1.11)
В соответствии с определением нижнее значение игры будет равно
=maxx H(x,y(x))= H(x*,y(x*)), (1.12)
где x* - максиминная стратегия 1-го игрока.
Подставляя в неравенство (1.11) x=x*, получим H(x*,y(x*))≤H(x*,y), и с учетом (1.12), получим неравенство
≤ H(x*,y) для всех y из Sy. (1.13)
Зафиксируем смешанную стратегию y из множества Sy и обозначим H(x(y),y) наибольшее значение функции H(x,y) на компактном ограниченном множестве Sx. Тогда для всех x из Sx и y из Sy выполняется неравенство
H(x(y),y)≥ H(x,y) (1.14)
В соответствии с определением нижнее значение игры будет равно
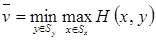=miny H(x(y),y)= H(x(y*),y*) (1.15)
где y* - минимаксная стратегия 2-го игрока.
Подставляя в неравенство (1.14) y= y*, получим H(x(y*),y*)≥H(x,y*), с учетом (1.15), получим неравенство
≥ H(x,y*), (1.16)
верное для всех x из Sx.
Подставляя в неравенство (1.13) y= y*, и в неравенство (1.16) x=x*, получим неравенства
≤ H(x*,y*) и 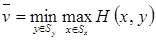≥ H(x*,y*),
откуда следует
≤ H(x*,y*)≤ 
(1.17)
Теорема доказана.
В соответствии с принципом гарантированного результата первый игрок ищет максиминную стратегию 
, при которой его выигрыш будет не меньше, чем нижнее значение игры, т.е. для любых 
выполняется неравенство (1.18)
Аналогично, второй игрок ищет минимаксную стратегию 
, при которой его проигрыш будет не больше, чем верхнее значение игры, т.е. для любых 
выполняется неравенство (1.19)
Для того, чтобы применение стратегий , давало игрокам гарантированные результаты, необходимо, чтобы выполнялись неравенства
(1.20)
т.е., чтобы исход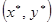 
был равновесным. Как доказано в теореме 3, для этого необходимо и достаточно, чтобы выполнялись равенства
(1.21)
то есть необходимо и достаточно, чтобы нижнее значение игры было равно верхнему значению игры 
(1.22)
Примем без доказательства теорему 4.
Теорема 4.
В любой матричной игре нижнее значение игры в смешанных стратегиях равно верхнему значению игры в смешанных стратегиях, т.е. 
.
Теорема (4) доказывает существование решения матричной игры в смешанных стратегиях. Число v называется значением игры в смешанных стратегиях.
Равновесные стратегии и называют оптимальными стратегиями, имея в виду, что критерием оптимальности служит принцип гарантированного результата.
Совокупность v (значение игры) и 
(оптимальные стратегии) называют решением игры в смешанных стратегиях.
Решение игры обладает следующими свойствами:
Свойство 1. Пусть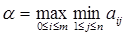 
– нижнее значение игры в чистых стратегиях, а 
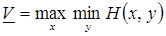– нижнее значение игры в смешанных стратегиях. Тогда
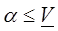
Доказательство.
По определению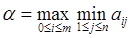 
. Пусть максимум по i достигается при i=i~, тогда для всех j=1.2…,n верно неравенство
α≤ai~j (1.23)
Возьмем произвольную смешанную стратегию y={ y1, y2,…, yn} из Sy. тогда справедливо 
. Умножим обе части неравенства (1.23) на yj≥0 и просуммируем по индексу j от 1 до n, получим неравенство
α≤∑ai~j yj (1.24)
Введем вектор x~={x~1, x~2,…, x~m}, где x~i=1, если i= i~ и x~i=0, если i ≠ i~. Вектор x~ удовлетворяет свойствам смешанной стратегии, поэтому положим, что x~ принадлежит множеству Sx. Преобразуем правую часть неравенства (1):
∑ai~j yj=∑∑ai~j x~i yj =Η(x~,y)
Тогда из неравенства (1.24) следует, что для любой смешанной стратегии y из Sy справедливо неравенство
α≤ Η(x~,y) (1.25)
По определению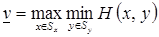 
. Обозначим H(x,y(x)) наименьшее значение функции H(x,y) на множестве Sy, тогда для всех x из Sx будет верно неравенство
≥ H(x,y(x)), подставляя в последнее неравенство x=x~, получим
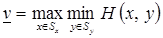≥ H(x~,y(x~)) (1.26)
В неравенство (1.25) подставим y= y(x~), получим
α≤ Η(x~, y(x~) (1.27)
Из неравенств (1.26) и (1.27) следует 
., что и требовалось доказать
Свойство 2. Пусть 
– верхнее значение игры в чистых стратегиях, а 
– верхнее значение игры в смешанных стратегиях. Тогда
Доказывается аналогично свойству 1.
Свойство 3. Нижняя чистая цена игры и верхняя чистая цена игры ограничивают значение сверху и снизу значение игры в смешанных стратегиях: 
.
Доказательство следует из теоремы (4) и свойств (1) и (2).
Свойство 4. Если матричная игра имеет равновесие в чистых стратегиях, то чистое значение игры 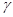равно значению игры в смешанных стратегиях, то есть при 
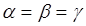будет справедливо
Доказательство следует из свойства (3).
В случае, когда матричная игра имеет седловую точку, оптимальная смешанная стратегия первого игрока будет иметь вид
.
И оптимальная смешанная стратегия 2-го игрока будет иметь вид
.
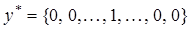Таким образом, равновесия в чистых стратегиях является частным случаем равновесия в смешанных стратегиях.
5. Теорема об активных стратегиях.
Стратегия i первого игрока называется его активной стратегией, если в оптимальной стратегии вероятность 
. Аналогично стратегия j игрока 2 называется его активной стратегией, если в оптимальной стратегии 
вероятность 
.
Теорема 5. Если один из участников игры применяет свою оптимальную стратегию, то ожидаемый выигрыш останется неизменным и равным v независимо от характера действий другого участника игры в пределах его активных стратегий.
Доказательство. Обозначим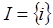 
для каждых 
, где 
– множество оптимальных стратегий первого игрока; 
для каждых 
, где 
– множество оптимальных стратегий второго игрока. Пусть второй игрок выбрал чистую стратегию 
тогда величина среднего выигрыша будет равна 
. Данный средний выигрыш достигается в том случае, когда первый игрок выбирает свою оптимальную стратегию 
а второй игрок реализует чистую стратегию из числа активных. Очевидно, что
.
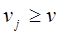С другой стороны, по определению значение игры будет равно
Таким образом, получаем систему
Это условие может выполняться только в случае, когда
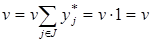
Теорема доказана.
|
|
|
