 |
Повторяющиеся игры. Применение к микроэкономике.
|
|
|
|
Пусть одни и те же условия игры с теми же игроками воспроизводятся многократно. В таком случае мы имеем расширение игры, которое называют повторяющейся игрой. Нетрудно заметить, что в повторяющейся игре смешанные стратегии могут применяться как частоты использования чистых стратегий. Возможность использования смешанных стратегий не является единственным преимуществом повторяющейся игры.
При повторении одной и той же игровой ситуации (при многократном разыгрывании игры) изменяются мотивы рационального поведения участников игры: во-первых, каждый из участников получает представление о предпочтениях другого участника; во-вторых, каждый участник, выбирая свою стратегию на некотором n -м шаге, даёт ответ на выбор другого участника на 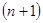 шаге. В игре возникают коммуникации между участниками. Подавая сигнал в виде выбранной на очередном шаге стратегии, этого, участник может влиять на выбор стратегии партнером на следующем шаге. Таким образом, в повторяющейся игре возникают предпосылки к совместному выбору стратегий, т.е. кооперации. Однако, существование этих предпосылок совсем не гарантирует того, что участники игры смогут кооперироваться.
шаге. В игре возникают коммуникации между участниками. Подавая сигнал в виде выбранной на очередном шаге стратегии, этого, участник может влиять на выбор стратегии партнером на следующем шаге. Таким образом, в повторяющейся игре возникают предпосылки к совместному выбору стратегий, т.е. кооперации. Однако, существование этих предпосылок совсем не гарантирует того, что участники игры смогут кооперироваться.
Эти обстоятельства имеют большое значение при анализе рынков с олигополистической конкуренцией (дуополия). Рассмотрим пример.
Пример. «Назначение цены». Две фирмы, выпускающие однотипный продукт, конкурируют друг с другом, устанавливая различные цены на свою продукцию. Выпуски фирм считаем заданными и неизменными. Такая конкуренция двух дуополистов называется ценовой конкуренцией или конкуренцию по Бертрану [3].
Для простоты будем считать, что каждая фирма выбирает одну из двух стратегий: низкая цена, высокая цена. Будем также считать, что фирмы назначают цену в начале каждого месяца независимо друг от друга. Так как продукт фирм однотипен, то потребитель будет осуществлять выбор, исходя только из цены. Та фирма, которая назначит более высокую цену, понесет убытки. С другой стороны, более высокая цена даст большую прибыль при условии, что на продукцию фирмы будет спрос. Прибыли фирм для каждого из возможных исходов приведем в таблице 9.
|
|
|
Таблица 9
| фирма 1 | |||||||
| низкая цена | высокая цена | ||||||
| фирма 2 | низкая цена | 10; 10 | 100; -50 | ||||
| высокая цена | -50; 100 | 50; 50 | |||||
Решение. Выпишем матрицу игры и найдём равновесие по Нэшу.
Таблица 10
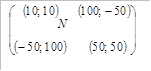
Равновесным по Нэшу исходом будет (10;10), а равновесными стратегиями – назначение низкой цены. Таким образом, дуополия Бертрана дает тот же эффект, что и совершенная конкуренция – снижение цены до уровня предельных издержек. Что мешает фирмам принять наиболее эффективную для них стратегию высоких цен с выигрышами? Исход (50;50) не является равновесным по Нэшу, поэтому, даже если фирмы договорятся об установлении высокой цены, каждой фирме в отдельности будет выгодно снижать цену. Ценовый сговор запрещён антимонопольным законодательством, но дуополия Бертрана показывает, что препятствием для сговора служит конкуренция. «Сговор разрушается зубилом конкуренции»э
Известны, однако, практические примеры, что олигополии воздерживаются от снижения цены в течение длительного времени. Следовательно, у фирм в условиях олигополии есть возможность координации действий. Как осуществляется эта координация, и может ли возникать исход, равновесный по Нэшу и эффективный по Парето?
Р. Аксельрод дал ответ на этот вопрос, предложив в повторяющейся игре стратегию «Зуб за зуб». Рассмотрим эту стратегию на примере «Дилемма заключенных» (таблица 333), предполагая, что данная ситуация разыгрывается бесконечное число раз.
|
|
|
Таблица 11
| стратегии второго заключенного | ||||
| стратегии первого заключенного | 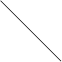 2 2
| сознаться | не сознаться | |
| сознаться | -4; -4 | -1; -7 | ||
| не сознаться | -7; -1 | -2; -2 | ||
Обозначим t=0,1,2… очередной шаг игры, Hit – выигрыш игрока i (i=1,2) на шаге t, Hit принимает значения из таблицы 333 в зависимости от стратегий игроков на шаге t. Эти стратегии будем обозначать Sit (i=1,2). Выигрыш каждого игрока i (обозначим Hi) будет складываться из его выигрышей на всех шагах игры Hit, однако, с учетом дисконтирования (снижения цены) выигрыша на каждом последующем шаге. Дисконтированные суммы часто применяются в экономических расчетах и основаны на соображении, что будущие прибыли значат для их получателя меньше, чем прибыли в настоящий момент, то же касается и убытков. Потому будем считать, что выигрыш игрока i на шаге t будет им оцениваться в момент (t-1), как величина d·Hit, где 0<d<1. Величина d называется коэффициентом дисконтирования. Дисконтированная сумма выигрыша игрока i от всей игры будет определяться по формуле
Hi= Hi0+ d·Hi1+ d2·Hi2 +…+ dt·Hit+… (2.13)
Стратегия «Зуб за зуб» состоит в следующем выборе стратегий Sit (i=1,2) на каждом шаге t:
Если на шаге (t-1) хотя бы один из игроков применил стратегию «сознаваться», то стратегия Sit будет «сознаваться»;
Если на шаге (t-1) оба игрока применили стратегию «не сознаваться», то стратегия Sit будет «не сознаваться».
Очевидно, что результат всей игры будет зависеть от стратегий, выбранных игроками на начальном шаге t=0.
Если S1,0= «сознаваться» и S2,0= «сознаваться», то все последующие стратегии будут «сознаваться», тогда
H1= H2= -4 - d·4 - d2·4-…- dt·4-…=-4/(1- d), (2.14)
по формуле суммы геометрической прогрессии.
Если S1,0= «не сознаваться» и S2,0= «не сознаваться», то все последующие стратегии будут «не сознаваться», тогда
H1= H2= -2 - d·2 - d2·2-…- dt·2-…=-2/(1- d). (2.15)
Если S1,0= «сознаваться» а S2,0= «не сознаваться», то все последующие стратегии будут «сознаваться», тогда
H1= -1 - d·4 - d2·4-…- dt·4-…=-1-4d /(1- d), H2=-7-4d /(1- d). (2.16)
Если S1,0= «не сознаваться» а S2,0= «сознаваться», то все последующие стратегии будут «сознаваться», тогда
H2= -1 - d·4 - d2·4-…- dt·4-…=-1-4d /(1- d), H1=-7-4d /(1- d). (2.17)
|
|
|
Таким образом, в зависимости от начальных стратегий игроков возможны 4 исхода, представленные в таблице 12.
Таблица 12
| стратегии второго заключенного | ||||
| стратегии первого заключенного |  2 2
| сознаться | не сознаться | |
| сознаться | -4/(1- d); ----4/(1- d) | -1-4d /(1- d); -7-4d /(1- d) | ||
| не сознаться | -7-4d /(1- d); -1-4d /(1- d) | -2/(1- d); -2/(1- d) | ||
Исход (-2/(1- d);-2/(1- d)) является оптимальным по Парето, этот исход будет равновесным по Нэшу тогда и только тогда, когда справедливо неравенство -2/(1- d)≥-1 -4d/(1- d), что верно при d≥1/3.
Итак, при достаточно большом коэффициенте дисконтирования стратегия «Зуб за зуб» делает наиболее благоприятный для всех игроков исход равновесным по Нэшу: если один заключенный не сознается, то другому также выгодно не сознаваться.
Применительно к примеру «Назначение цены» стратегия «Зуб за зуб» имеет следующий смысл. Если игра «Назначение цены» разыгрывается бесконечное число раз, то один из предпринимателей начинает с высокой цены и удерживает её до тех пор, пока второй предприниматель тоже придерживается высокой цены. Если второй назначит низкую цену, то первый тоже понизит свою цену. На практике существует возможность, что если второй предприниматель осознает свою ошибку и вернётся к высокой цене, то первый поступит также.
Стратегия «Зуб за зуб» позволяет достигать эффективного по Парето исхода, если игра повторяется бесконечное число раз. В реальности ни один процесс в экономике не длится бесконечно долго, поэтому предположение о бесконечном числе разыгрывания не реалистично.
Предположим, что игра «Назначение цены» разыгрывается конечное число раз, например 5 лет (60 месяцев). Как изменится рациональные соображения участников при конечном числе разыгрывания? Каждый участник игры выбирает стратегию «Зуб за зуб», потому что, отклонившись от неё в n -м периоде, он будет наказан в 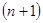 периоде. Однако в данном случае 60-й период является последним. Воспроизведём логику рассуждений первого участника игры: «Если я буду сохранять высокую цену 59 периодов, а в 60-м назначу низкую цену, то я получу дополнительный выигрыш, а другие участники не успеют меня наказать за отклонение от общей стратегии». Далее первый участник может предполагать, что другие игроки рассуждают аналогично, следовательно, есть смысл первому нарушить негласный договор. Тогда первый участник склонен отклониться от общей стратегии уже в 59-м, а не в 60-м периоде, и т.д. Таким образом, стратегия «Зуб за зуб» теряет устойчивость на протяжении всего разыгрывания.
периоде. Однако в данном случае 60-й период является последним. Воспроизведём логику рассуждений первого участника игры: «Если я буду сохранять высокую цену 59 периодов, а в 60-м назначу низкую цену, то я получу дополнительный выигрыш, а другие участники не успеют меня наказать за отклонение от общей стратегии». Далее первый участник может предполагать, что другие игроки рассуждают аналогично, следовательно, есть смысл первому нарушить негласный договор. Тогда первый участник склонен отклониться от общей стратегии уже в 59-м, а не в 60-м периоде, и т.д. Таким образом, стратегия «Зуб за зуб» теряет устойчивость на протяжении всего разыгрывания.
|
|
|
Существуют, однако, предпосылки для того, чтобы стратегия «Зуб за зуб» применялась на олигополистическом рынке. Предположим, что фирма 1 имеет хотя бы небольшие сомнения в том, что ее конкурент абсолютно рационален, т.е. в том, что он просчитал всю логическую цепочку. Тогда фирма 1 будет сомневаться, в том, что конкурент назначит низкую цену в последнем периоде, тогда фирме 1 нет смысла отказываться от высокой цены в предпоследнем периоде и т.д. Имеются практические примеры, как устойчивости, так и неустойчивости стратегии «Зуб за зуб».
Пример относительной устойчивости: «Рынок водомерных счётчиков» [4]
Производителями на рынке водомеров в США на протяжении более чем 30 лет были 4 фирмы, одна из которых имела долю на рынке примерно в 35%, остальные три вместе – от 50 до 55%. Особенность рынка водомеров в том, что спрос (его представляли коммунальные службы муниципалитетов) был неэластичен и стабилен. Так же стабильными были издержки производителей. Продукция однотипная, так что рынок водомеров можно рассматривать как пример однородной олигополии. При таких условиях четыре фирмы могли бы получать высокую монопольную прибыль. Общая ценовая стратегия фирм – назначение высокой цены – наблюдалась в течение шести лет. Прямой сговор не мог реализоваться в силу действия антимонопольного закона, но фирмы могли довольно долго следовать стратегии «Зуб за зуб».
Пример неудачи при выработке общей ценовой стратегии: «Рынок авиаперевозок» [5].
В 1983 году президент компании «American Airlines» предложил другим авиакомпаниям использовать единую схему образования тарифов в зависимости только от расстояния между аэропортами. Цель состояла в ограничении ценовой конкуренции и достижении неявного сговора в ценообразовании. Большая часть авиакомпаний отнеслась доброжелательно к предложенному плану. Однако, в итоге план был сорван, т.к. компания «Pan Am», недовольная своей долей рынка начала снижать цены, вводя различные скидки, и вскоре ей последовали другие компании. Разыгралась «Дилемма заключенных, или, как выразился один из экономистов, сговор был нарушен зубилом конкуренции.
|
|
|
При ограниченном количестве розыгрышей стратегия «Зуб за зуб» теряет устойчивость. Всё же в отдельных случаях она может оказаться эффективной. Предпосылки стратегии «Зуб за зуб»:
1. Малое число компаний и удовлетворённость каждой из них совей долей рынка;
2. Стабильный спрос и издержки;
- Участники игры сомневаются в том, их конкуренты способны всё рационально подсчитать. Например, первый участник, сомневаясь в том, что второй участник абсолютно рационален, думает: «Может быть, он не сообразит снижать цену в 60-м периоде, тогда мне выгоднее придерживаться стратегии «Зуб за зуб» на протяжении 59 периодов».
Последовательные игры
До сих пор мы предполагали, что участники игры делают свои ходы одновременно, т.е. одновременно выбирают свои стратегии. Однако, во многих случаях, дело обстоит так, что игроки делают ходы поочерёдно. Такие игры называются последовательными играми. Для их описания больше всего подходит развёрнутая форма игры, т.е. ее представление в виде дерева игры.
Рассмотрим в качестве примера последовательную игру двух участников. Пусть первый ход принадлежит первому игроку, который имеет две стратегии; второй участник ходит вторым и имеет три стратегии. Дерево этой игры изображено на рис. 1:
Рисунок 1
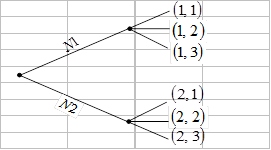
В данной игре первый игрок может оптимизировать свой выигрыш, проводя следующие вычисления. Сравниваются три исхода (1,1), (1,2) и (1,3). Пусть наибольшее значение выигрыша второго игрока достигается при исходе (1,2). Аналогично сравниваются три исхода (2,1), (2,2) и (2,3). Пусть наибольшее значение выигрыша второго игрока достигается при исходе (2,3). Тогда второй игрок, действуя рационально, в ответ на первую стратегию первого игрока выберет стратегию, при которой реализуется исход (1,2) а в ответ на вторую стратегию первого игрока выберет стратегию, при которой реализуется исход (2,3). Таким образом, первый игрок приходит к выводу, что если он выберет первую стратеги, то его выигрыш составит  , а если он выберет вторую стратегию, то выигрыш будет равен
, а если он выберет вторую стратегию, то выигрыш будет равен 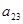 . Если
. Если 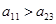 , то первому игроку выгоднее придерживаться первой стратегии, а если
, то первому игроку выгоднее придерживаться первой стратегии, а если  , то первому игроку выгоднее придерживаться второй стратегии.
, то первому игроку выгоднее придерживаться второй стратегии.
Данный тип оптимальности называется оптимальностью по Штакельбергу.
Исход игры 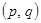 называется равновесием по Штакельбергу, а стратегии
называется равновесием по Штакельбергу, а стратегии 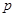 и
и 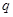 первого и второго игроков соответственно называются оптимальными по Штакельбергу, если
первого и второго игроков соответственно называются оптимальными по Штакельбергу, если 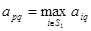 , где
, где 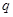 определяется из уравнения
определяется из уравнения 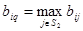
Пояснение. Уравнение 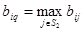 означает, что стратегия
означает, что стратегия 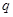 является лучшим ответом второго участника на стратегию
является лучшим ответом второго участника на стратегию 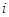 первого участника, т.е.
первого участника, т.е.
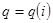 .
.
Уравнение 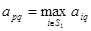 означает, что первый участник выбирает стратегию таким образом, что в случае рационального выбора второго участника, первый участник получит свой наибольший выигрыш. Здесь мы предполагаем, что право первого хода принадлежит первому участнику. Аналогично можно сформулировать определение оптимальной стратегии по Штакельбергу в случае, если первый ход принадлежит второму участнику. В некоторых играх право первого хода даёт преимущество тому участнику, который им обладает.
означает, что первый участник выбирает стратегию таким образом, что в случае рационального выбора второго участника, первый участник получит свой наибольший выигрыш. Здесь мы предполагаем, что право первого хода принадлежит первому участнику. Аналогично можно сформулировать определение оптимальной стратегии по Штакельбергу в случае, если первый ход принадлежит второму участнику. В некоторых играх право первого хода даёт преимущество тому участнику, который им обладает.
Пример. «Игра на опережение».
Ситуация дуополии на рынке фирм-производителей сухих завтраков. Обе фирмы выпускают одинаковую продукцию: сырки и хлопья. Первая фирма доминирует на рынке и первой приступает к выпуску продукта. Прибыли обеих фирм приведены в таблице 13:
Таблица 13
| Вторая фирма | |||||||
| сырки | хлопья | ||||||
| первая фирма | сырки | 5; 5 | 10; 30 N2 | ||||
| хлопья | 30; 10 N1 | 5; 5 | |||||
Найти равновесие по Штакельбергу.
Решение. В игре существует два равновесия по Нэшу  . Если бы фирмы выбирали продукты одновременно, то равновесием в игре было бы равновесие по Нэшу. Вспомним, что первая фирма обладает правом первого хода и запишем развёрнутую форму игры (рис. 2)
. Если бы фирмы выбирали продукты одновременно, то равновесием в игре было бы равновесие по Нэшу. Вспомним, что первая фирма обладает правом первого хода и запишем развёрнутую форму игры (рис. 2)
Рисунок 2

Двигаясь по дереву игры от конца к началу, мы приходим к выводу, что оптимальной стратегией по Штакельбергу для первой фирмы будет выбор сырков, а для второй - хлопьев. Таким образом, равновесие по Штакельбергу достигается в исходе  .
.
Легко проверить, что равновесие по Нэшу всегда является равновесием по Штакельбергу (иллюстрацией служит пример «Игра на опережение»), но обратное не всегда верно.
Также преимущества первого хода проявляется в конкуренции по Курно[6] между двумя фирмами. Дуополия по Курно представляет собой модель, в которой два конкурирующих производителя однородной продукции выбирают свой выпуск, исходя из заданной функции совокупного спроса и из предположения, что конкурент максимизирует свою прибыль, принимая выпуск другой фирмы является постоянным. Таким образом, фирмы начинают с монопольной цены, а затем последовательно снижают цены до равновесного значения. Рассмотрим пример.
Пример. «Дуополия Курно»
Рынок поделён между двумя фирмами, каждая из которых выбирает свой объём выпуска: 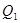 – выпуск первой фирмы;
– выпуск первой фирмы; 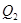 – выпуск второй фирмы. Совокупный выпуск (предложение) будет равен
– выпуск второй фирмы. Совокупный выпуск (предложение) будет равен
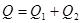 (2.18)
(2.18)
Уравнение кривой спроса на данном рынке задано и имеет вид:
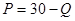 (2.19)
(2.19)
Требуется определить равновесную цену, если право первого хода принадлежит первой выпуск.
Решение. По формуле 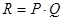 найдём выручку первой фирмы
найдём выручку первой фирмы

 (2.20)
(2.20)
Аналогично, выручка второй фирмы будет равна:
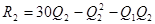 (2.21)
(2.21)
По формуле вычисления прибыли 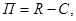 находим прибыль каждой из фирм:
находим прибыль каждой из фирм:
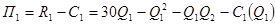 ,
,
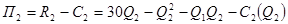 .
.
Предположим сначала, что каждая фирма является монополистом, следовательно, может выбирать выпуск, максимизирующий ее прибыль при постоянном выпуске конкурента. Оптимум (максимум прибыли) достигается в точке, где предельная выручка равна предельным издержкам 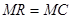 , т.е.:
, т.е.:
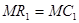

Для упрощения будем считать, что
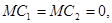
тогда первая фирма выбирает выпуск 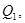 при котором
при котором  . Вторая фирма выбирает выпуск
. Вторая фирма выбирает выпуск 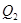 , при котором
, при котором 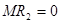 .
.
Предельная выручка фирм определяется как частная производная от выручки по объёму выпуска. Таким образом:
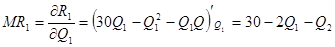
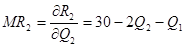
Найдём значение оптимальные значения 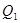 и
и 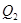
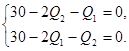 (2.22)
(2.22)

Система (2.22) получается в предположении, что каждая фирма максимизирует свою выручку и предполагает, что её конкурент сделает то же самое.
Находим значение 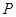 и выручки обеих фирм:
и выручки обеих фирм:
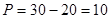
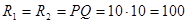
Если бы фирмы могли договориться между собой, то они бы выбрали такой выпуск  , который максимизировал бы их общую выручку
, который максимизировал бы их общую выручку
 .
.
При этом 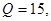 а выпуск каждой из фирм, при справедливом дележе, был бы равен
а выпуск каждой из фирм, при справедливом дележе, был бы равен  . Однако реализации этого исхода препятствует очередность ходов, которая дает преимущества фирме, обладающей правом первого хода.
. Однако реализации этого исхода препятствует очередность ходов, которая дает преимущества фирме, обладающей правом первого хода.
Для простоты, будем считать, что каждая фирма выбирает один из трёх объёмов выпуска: 7,5; 10 и 15. В таблице 14 приведены выручки каждой из фирм для всех всевозможных исходов:
Таблица 14
| вторая фирма | |||||||||
| 7,5 | |||||||||
| первая фирма | 7,5 | 12,5; 12,5 | 97,75; 125 | 65,25; 112,5 | |||||
| 125; 93,75 | 100; 100 | 50; 75 | |||||||
| 112,5; 56,25 | 75; 50 | 0; 0 | |||||||
Равновесным по Нэшу является исход с результатами (). Теперь предположим, что первая фирма обладает правом первого хода, т.е. она выбирает объём выпуска и сообщает об этом второй фирме, которая, в свою очередь, выбирает объем выпуска, максимизирующий прибыль при заданном объеме выпуска конкурента. Таким образом, получаем следующие исходы:
§ первая фирма – 7,5; тогда вторая фирма – 10, результат (93,75; 125);
§ первая фирма – 10; тогда вторая фирма – 10, результат (100; 100);
§ первая фирма – 15; тогда вторая фирма – 7,5, результат (112,5; 56,25).
Сравнивая полученные исходы по прибыли первой фирмы, находим равновесие по Штакельбергу, находящееся в исходе с результатами 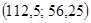 , выпуски фирм при этом
, выпуски фирм при этом 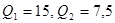 . Первая фирма выигрывает за счёт права первого хода, вторая фирма при этом теряет часть прибыли по сравнению с равновесием по Нэшу..
. Первая фирма выигрывает за счёт права первого хода, вторая фирма при этом теряет часть прибыли по сравнению с равновесием по Нэшу..
В реальности первая фирма, выбрав объём производства 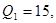 должна убедить вторую фирму в том, что она не намерена отступать от этой стратегии. Для этого она может проводить рекламную компанию, вкладывать деньги и т.д. такие действия называются стратегическим ходом.
должна убедить вторую фирму в том, что она не намерена отступать от этой стратегии. Для этого она может проводить рекламную компанию, вкладывать деньги и т.д. такие действия называются стратегическим ходом.
Стратегическим называется ход, который влияет на выбор другого игрока в благоприятном направлении для игрока, делающего стратегический ход.
Влияние заключается в том, что стратегический ход воздействует на ожидание второго игрока относительно поведения первого. Таким образом, стратегический ход ограничивает выбор партнёра, предварительно ограничив собственное поведение. Делая стратегический ход, участник игры связывает себя обещаниями, вкладывает средства в действия, которые вынуждают партнёра выбирать благоприятные для первого участника стратегии. Но может оказаться, что второй участник не поверит стратегическому ходу первого игрока и сочтёт его действия пустой угрозой.
Пример. «Пустые угрозы при наличии доминирующих стратегий»
На рынке действуют две фирмы. Первая фирма производит многофункциональные мобильные телефоны, а вторая – простые. Если вторая фирма назначит низкую цену, то часть покупателей первой фирмы перейдёт на потребление продукции второй фирмы. Если же первая назначит низкую цену, то у второй фирмы останется лишь один выход – назначить более низкую, чем у первой фирмы цену. Прибыли фирм в зависимости от выбранных стратегий приведены в таблице 15.
Таблица 15
| Вторая фирма | |||||||
| высокая цена | низкая цена | ||||||
| первая фирма | высокая цена | 100; 80 | 80; 100 | ||||
| низкая цена | 20; 0 | 10; 20 | |||||
Имеет ли первая фирма возможность добиться выигрыш 100 с помощью стратегического хода?
Решение.
Для решения следует ответить на следующие вопросы:
1. Имеет ли вторая фирма доминирующие стратегии?
Вторая фирма имеет одну доминирующую стратегию – низкая цена.
2. Что является следствием из этого?
Какие бы действия не предпринимала первая фирма, вторая фирма будет назначать низкую цену.
3. Какая из фирм доминирует на рынке?
Доминирующей на рынке является первая фирма, т.к. её продукция является более разнообразной.
4. Как будут восприняты второй фирмой действия первой, которые она может предпринять для того, чтобы убедить вторую фирму назначить высокие цену?
Как пустые угрозы.
5. Почему второй фирме не стоит воспринимать угрозы первой всерьёз?
Что бы ни делала первая фирма, вторая фирма знает, что первой фирме, при снижении цены на свою продукцию, будет только хуже.
6. Что изменится, если вторая фирма знает, что у первой фирмы репутация рискованного иррационального игрока?
В этом случае вторая фирма может поверить угрозам первой фирмы.
В данном случае реализации наиболее выгодного для первой фирмы равновесия по Штакельбергу мешает наличие доминирующих стратегий у второй фирмы.
Пустые угрозы могут быть также следствием равновесия по подыграм (Sub games Equilibrium), что демонстрирует пример «Заложник – террорист»
Пример: Пустые угрозы в игре “заложник-террорист”. Информированные агенты.
Террорист захватил заложника и требует от него выкуп, условный размер которого возьмем за 1. Террорист угрожает взорвать заложника вместе с собой, если выкуп не будет выплачен. Оба участника знают потери друг друга при неблагоприятном исходе игры, т.е. при взрыве. Какое решение должен принять заложник?
Решение. Изобразим дерево решений (рис. 3), и разобьем игру на подыгры.
Рисунок 3
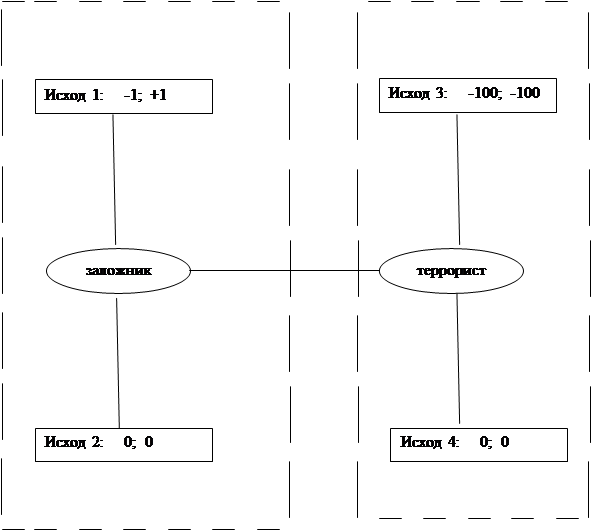
Subgame2 Subgame1
1 платить выкуп 3 взрывать
2 не платить выкуп 4 не взрывать
В подыгре 1 (Subgame1) террорист имеет доминирующую стратегию «не взрывать».
В подыгре 2 (Subgame2) заложник имеет доминирующую стратегию «не платить».
|
|
|


