Решение игры в смешанных стратегиях

Пусть задана матричная антагонистическая игра. Требуется найти решение игры в смешанных стратегиях, т.е. требуется найти значение игры v, оптимальную стратегию первого игрока оптимальную стратегию второго игрока .

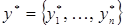Решение. Запишем матрицу игры

 

	смеш. стр. второго игрока
смеш. стр. первого игрока

 

Из теоремы об активных стратегиях (теорема 5) следует, в частности, что применение одним из игроков своей оптимальной стратегии против любой чистой стратегии противника даёт результат не хуже, чем значение игры V. Результат для первого игрока должен быть , а результат для второго . Тогда первый игрок решает задачу нахождения решения , удовлетворяющего условиям:

 

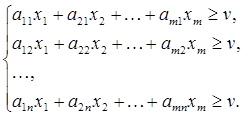(1.28)

Второй игрок решает задачу нахождения решения , удовлетворяющего условиям:

(1.29)

Задачи первого и второго игроков вместе образуют двойственную задачу линейного программирования. Такие задачи решаются с помощью двойственного симплекс-метода. В частности, можно доказать, что сформулированная выше двойственная задача линейного программирования имеет решение для любых платёжных матриц.

Из этого следует, что любая матрица антагонистической игры имеет решение в смешанных стратегиях. Для частного случая, когда матрица игры имеет размеры , смешанные стратегии можно найти графическим методом. Действительно, пусть матричная игра задана Таблицей 6.

Таблица 6

	смеш. стр. второго игрока
смеш. стр. первого игрока

 

Сформулируем задачу для первого и второго игроков

(1.30) (1.31)

Решим задачу для первого игрока. Обозначим тогда

Решим полученную задачу линейного программирования графически в осях v и X (Рис.2):

Рисунок 2

Свойства игры в смешанных стратегиях.

1. Решение игры не изменится при вычёркивании доминируемых стратегий.

2. Решение игры не изменится при добавлении доминируемых стратегий.

3. Решение игры не изменится при перестановке местами строк (столбцов) платёжной матрицы. Т.е. игроки могут нумеровать свои стратегии в любом порядке. Смысл игры и её решение от этого не изменится.

Игра против природы

Смысл игры против природы состоит не в том, что игрок вредит окружающей среде, и не в том, что природа враждебна игроку, а в том, что игрок выбирает своё решение, не зная состояния внешней среды, от которых зависит его выигрыш, т.е. в условиях неопределённости. Эта неопределённость вызвана внешними случайными факторами – природными, социальными, техническими, политическими, экономическими. Всю совокупность перечисленных случайных факторов принято называть природой (Nature).

Предположим, что экономический субъект выбирает свои стратегии из некоторого множества 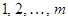. Он знает, что внешний мир (природа), независимо от его действий, может находиться в одном из состояний . Эти состояния можно условно считать стратегиями природы. Каждое из состояний природы в сочетании со стратегией экономического субъекта (игрока) приводит к определённым исходам. Каждый исход оценивается игроком в зависимости от полезности для него этого исхода. Таким образом, множество исходов и заданная на них функция полезности экономического субъекта задают платёжную матрицу с элементами – выигрыш (полезность) экономического субъекта при выборе им стратегии iи состоянии природы j.

Следовательно, игра против природы является частным случаем матричной игры. Её особенность состоит в том, что второй игрок (природа) не преследует собственные цели, то есть является безразличным игроком. Стратегии природы являются ее возможными состояниями, определяемыми объективными законами, а также случайными, неизвестными игроку факторами. То, что у природы нет собственных интересов, отнюдь не облегчает задачу принятия решений, потому что в игре против природы нельзя предусмотреть ее стратегии, исходя из ее «интересов». Модели выбора решения в игре против природы делятся на два типа. Во-первых, это модели выбора при определенном критерии оптимальности, применяемые в тех случаях, когда смысл задачи не дает возможности игроку использовать смешанные стратегии. Во-вторых, это модели с использованием смешанных стратегий.

§2.1.7.Критерии оптимальности решения в условиях неопределённости

Рассмотрим задачу принятия решения, когда на стадии принятия решения ЛПР знает:

а) возможные состояния среды: у₁, у₂,.. у_n Є Y – множество состояний окружающей среды.

б) результат, к которому приведёт выбор альтернативы х Є Х для каждого возможного состояния среды: у₁, у₂,.. у_n,т. е. знает функцию выигрыша (проигрыша): f(х,y) для всех х Є Х, у = Y.

Х – множество альтернатив

Y – множество состояний среды

При этом ЛПР не располагает информацией о том, как распределены вероятности состояний среды и даже не знает, какие из этих состояний более вероятны. Такая ситуация принятия решений определяется как структурная неопределённость.

Задача выбора «наилучшего» решения требует определить критерий оптимальности. Очевидно, что широкое разнообразие жизненных и экономических ситуаций не может быть описано с помощью единственного критерия оптимальности, в математических моделях принятия решения предложены и исследованы несколько критериев оптимальности.

Сформулируем определение – что из себя должен представлять критерий оптимальности?

Для этого определения выделим следующие моменты:

1. Любой критерий оптимальности основан на определённых предположениях (гипотезах) о поведении окружающей среды.

2. Критерий оптимальности представляет собой правило выбора «наилучшего» решения.

Таким образом, критерий оптимальности – это правило выбора «наилучшего» решения в условиях неопределённости, основанное на определённых предположениях относительно поведения окружающей среды и предпочтений ЛПР.

При этом желательно, чтобы критерий оптимальности обладал свойствами, согласующимися со здравым смыслом и рациональностью. Чтобы пояснить, в чем состоит в данном случае рациональный подход, вспомним понятие доминируемости.

Пусть задача принятия решения характеризуется n-состояниями среды: у₁, у₂, ..у_n и предусматривает выбор из m-альтернатив: х₁, х₂, ..х_m. Причём для каждой пары (х_i, y_j) определено значение функции f(х_i, y_j).

Тогда задачу принятия решения можно описать с помощью платёжной матрицы (Таблица 7):

 

 

Таблица 7

Состояния среды Альтернативы	y1	y2	…	yj	…	yn
x1	f(x1,y1)	f(x1,y2)	…	f(x1,yj)	…	f(x1,yn)
x2	f(x2,y1)	f(x2,y2)	…	f(x2,yj)	…	f(x2,yn)
…	…	…	…	…	…	…
xi	f(xi,y1)	f(xi,y2)	…	f(xi,yj)	…	f(xi,yn)
…	…	…	…	…	…	…
xm	f(xm,y1)	f(xm,y2)	…	f(xm,yj)	…	f(xm,yn)

 

 

Предположим, что для некоторых целых чисел i и k Є [1,m] выполняется условие: для любого j f(x_i,y_j) ≥ f(x_k,y_j).

В строке i результаты больше, чем в строке k. Следовательно, стратегия x_i доминирует стратегию x_k, x_k – доминируемая стратегия.

Очевидно, что доминируемые стратегии (или альтернативы) заведомо хуже других, а доминирующие заведомо лучше. Отсюда следует, что первый принцип, которому должен удовлетворять критерий оптимальности, это принцип доминирования.

a) Принцип доминирования:

- если существует доминирующая стратегия, то критерий оптимальности должен обеспечивать выбор именно этой стратегии;

- если существуют доминируемые стратегии, то их удаление и введение не должно влиять на выбор наилучшей стратегии.

Так же очевиден смысл двух других принципов:

b) Перенумерация альтернатив (нумерация строк) и/или состояний среды (нумерация столбцов) не должна влиять на выбор наилучшей стратегии.

c) Предположим, что ко всем значениям функции выигрыша добавлено число а: f(x_i,y_j) + a. Очевидно, что критерий оптимальности должен обеспечивать выбор наилучшей стратегии, которая не зависит от прибавления аддитивной постоянной к функции выигрыша.

Рассмотрим наиболее часто применяемые критерии оптимальности.

§ 2.1.8 Критерий Лапласа

Критерий Лапласа основан на гипотезе, согласно которой все состояния среды реализуются с одинаковыми вероятностями.

Если возможна реализация 2-х состояний А и В и нет никакой информации об их вероятностях, то естественно предполагать, что:

Р(А) = Р(В) = ½.

Если среда может принимать состояния у₁, у₂,..у_n и нет информации о вероятностях этих значений, то естественно предполагать:

Р( у₁ ) = Р( у₂ ) =...= Р( у_n ) = 1/n.

Пусть для задачи принятия решения, заданной Таблицей 1, принята гипотеза равной возможности. Для каждой стратегии x_i определим значение функции L (x_i):

L (x_i) = 1/n*∑ f(x_i,y_j) (1.32)

Получим L(x₁), L(x₂),.. L(x_n) – среднеарифметические выигрыши для каждой стратегии.

Выбираемая стратегия x_i: L(x_l) ≥ L(x_i) (1.33)

Пример: Найти наилучшую стратегию по критерию Лапласа для задачи принятия решения, заданной платёжной матрицей Таблица 8:

Таблица 8

Легко показать, что критерий Лапласа удовлетворяет всем 3-м условиям, определённым в пункте 2.1.1.

Тем не менее, у критерия Лапласа есть недостаток: по критерию Лапласа может быть выбрана рискованная стратегия.

Маленькие значения выигрыша при нахождении среднего перекрываются большими – эффект компенсации.

 

§ 2.1.9. Критерий Вальда (максиминный критерий)

Выбор критерия Вальда основан на гипотезе, согласно которой ЛПР стремится получить гарантированный результат при любом состоянии среды.

Пример: Найти наилучшую стратегию по критерию Вальда для задачи принятия решения, заданной платёжной матрицей Таблица 9:

Таблица 9

Решение. Найдём выбор по принципу максимина: для любого i min f(x_i,y_j) = a_i – худший результат при выборе i.

maxmin f(x_i,y_j) = max a_i = K.

Легко показать, что критерий Вальда удовлетворяет всем 3-м условиям, определённым в пункте 2.1.1.

Недостаток этого критерия: критерий Вальда отвергает хорошие гипотезы из-за своего крайнего пессимизма.

 

§2 .1.10. Критерий Гурвица

(критерий взвешенного оптимизма /пессимизма)

В основе этого критерия лежит гипотеза о том, что уровень пессимизма ЛПР принимает некоторое значение α: 0 ≤ α ≤ 1. Чем больше α, тем пессимистичнее настроен ЛПР. Для каждой строки x_i определяется:

- число а_i = min f((x_i,y_j);

- число b_i = max f((x_i,y_j).

Затем для каждого значения x_i и α рассчитывается число:

H(x_i, α) = α* а_i + (1- α)* b_i

и выбирается max H(x_i, α) = h(α).

Пример 3: Для Примера 2 найти наилучшую стратегию по критерию Гурвица, при значении α = ½ Таблица 10.

Таблица 10

 

Очевидно, что если α = 1, то критерий Гурвица превращается в критерий Вальда.

Докажем, что критерий Гурвица удовлетворяет принципу доминирования.

Доказательство. Пусть стратегия x_i является доминирующей. Это значит, что для всех j, 1 ≤ j ≤ n и для всех k, 1 ≤ k ≤ m, k ≠ j, выполняется неравенство:

f(x_i,y_j) ≥ f(x_k,y_j). (1.34)

Из этого следует, что:

max f(x_i,y_j) ≥ max f(x_k,y_j). (*)

Докажем выполнение неравенства (*) подробнее:

max f(x_i,y_j) = f(x_i,y_p)

max f(x_k,y_j) = f(x_k,y_q)

f(x_i,y_j) ≤ f(x_i,y_p)

f(x_k,y_j) ≤ f(x_k,y_q)

 

Из (1.34) следует, что f(x_k,y_q) ≤ f(x_i,y_q) ≤ f(x_i,y_p).

Таким образом, получается b_k ≤ b_i.

Введём обозначения: min f(x_i,y_j) = а_i = f(x_i,y_l),

min f(x_k,y_j) = a_k = f(x_k,y_r)

Из неравенства доминирования (d) следует, что f(x_k,y_p) ≤ f(x_i,y_r)

а_i = f(x_i,y_l) ≥ f(x_k,y_l) ≥ min f(x_k,y_l) = a_k

а_i ≥ a_k

Так как α ≥ 0, 1- α ≥ 0, то:

α * а_i ≥ α * а_k

(1- α)* b_i ≥ (1- α)* b_k

Выполнение условий перестановки и аддитивной постоянной достаточно очевидно.

Недостаток критерия Гурвица: недостаточная обоснованность выбора параметра α (его значение основано на оценке отношения ЛПР к риску).

§ 2.1.11. Критерий Сэвиджа (критерий наименьших сожалений)

Критерий основан на гипотезе, что ЛПР предпочитает такое решение, при реализации которого у него возникают наименьшие сожаления.

Рассмотрим матричные игры, заданные Таблицей 1.

Если ЛПР думает, что среда примет какое-то определенное состояние y_j, он выберет стратегию, максимизирующую его выигрыш при данном состоянии среды y_j, Обозначим соответствующую стратегию x_l, тогда очевидно, что для всех стратегий x_i справедливо неравенство

f(x_l,y_j) ≥ f(x_i,y_j),

другими словами f(x_l,y_j) – наибольший элемент в столбце j.

Следовательно, для любого столбца j и любой строки i разность

r_ij= f(x_l,y_j)- f(x_i,y_j)

является неотрицательным числом и показывает потерю выигрыша ЛПР, если он выберет стратегию x_i, а среда примет состояние y_j.

Итак, критерий Сэвиджа даёт следующий алгоритм выбора наилучшего решения:

1) для всех y_j находят наилучшее решение для данного состояния:

с_j = max f(x_i,y_j)

2) для каждого исхода x_i для всех y_j находят значение потерь или сожалений:

r_ij = с_j - f(x_i,y_j)

3) получают матрицу потерь:

R = || r_ij ||

4) для каждой альтернативы находят наибольшее сожаление:

S_i = max r_ij

5) решаем задачу нахождения х_k:

S_k ≤ S_i

minmax r_ij

Пример: Найти решение оптимальное по критерию Сэвиджа для матрицы Таблица 11:

Таблица 11

	у1	У2	у3	у4	у5
х1
х2
maxi

1-1 6-3 8-2 7-4 9-5

c_ij =

1-0 6-6 8-8 7-7 9-9

 

 

0 3 6 3 4 6

c_ij =

1 0 0 0 0 1

 

max c_ij = 6 – наибольшее сожаление.

Можно показать, что критерий Сэвиджа удовлетворяет принципу доминирования, инвариантности при перестановке, инвариантности при добавлении аддитивной постоянной.

Критерий Сэвиджа отличается от критерия Вальда тем, что для критерия Сэвиджа реализуется принцип minmax для матрицы потерь, а для критерия Вальда - maxmin для матрицы выигрышей.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: