Эффективность обмена. Ящик Эджворта

Рассмотрим экономику, в которой имеется два участника, которые могут обмениваться двумя благами. Суммарное количество первого блага обозначим a, суммарное количество второго блага – b. Пусть первоначально первый участник имел набор благ , а второй – . Могут ли при этом участники улучшить своё нынешнее положение, обмениваясь между собой благами, т.е. вступать в коалиции? Будем считать, что заданы функции полезности: – для первого участника и 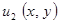– для второго. Будем также считать, что издержки на получение информации, заключение контрактов и поиск партнёров (трансакционные издержки) равны нулю.

Для ответа на этот вопрос Эджворт предложил свою модель – Ящик Эджворта.

 

 

Рисунок 1

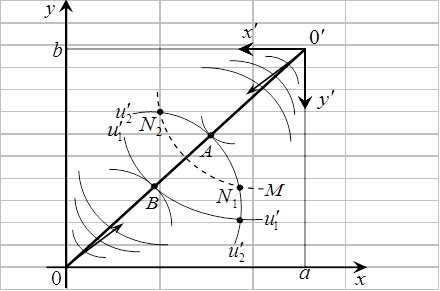
Изобразим карту кривых безразличия для каждого из участников (см. рис. 1). Можно ли улучшить положение первого участника, не ухудшая при этом положение второго.

В пределе мы получим точку A на кривой безразличия , в которой эта кривая касается кривой безразличия первого участника. Рассуждая аналогично, можно улучшить положение второго участника, не ухудшая при этом положение первого. Лучшее решение будет находиться в точке B, где кривая касается кривой . Таким образом, мы получим множество точек, в которых кривая безразличия первого участника касается кривой безразличия второго участника. Это множество точек лежит на кривой , которая называется контрактной кривой.

Рассмотрим контрактную кривую с точки зрения эффективности по Парето. На рис. 1., при переходе от точки M к точке A, первый участник улучшает своё положение, а положение второго остаётся неизменным; при переходе от точки M к точке B, положение второго участника улучшается, а положение первого остаётся неизменным. Таким образом, получается, что положение A предпочтительнее положения B, а положение B, в свою очередь, предпочтительнее положения M.

При переходе от A к B полезность одного из участников увеличивается, а полезность другого уменьшается. Такие решения называются Парето-несопоставимыми.

Множество решений, которые являются Парето-предпочтительными по сравнению с решениями, не входящими в данное множество, называют множеством Парето-эффективных решений. Таким образом, контрактная кривая является множеством решений, эффективных по Парето.

Пример. Вернёмся к вопросу об улучшении условий каждого участника при обмене.

Рисунок 2

Очевидно, что первый участник согласится на обмен, при котором его кривая безразличия сдвинется вверх и вправо (Рис.2), а второй участник, согласится на обмен, при котором его кривая безразличия сдвинется вниз и влево. Таким образом, множество эффективных обменов будет лежать на контрактной кривой между точками и . Этот участок объединяет множество решений, которые могут принимать участники в ходе переговоров (торга). Именно поэтому, это множество называется переговорным.

Найдём условие, которым удовлетворяют элементы переговорного множества. Условие Парето-эффективности означает, что игроки решают одну из двух задач. Либо первый игрок максимизирует свою полезность, при условии, что полезность второго игрока сохраняет своё стационарное значение, т.е. (задача 1), либо второй игрок максимизирует свою полезность при условии, что .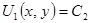

Какая именно из двух задач будет решаться, зависит от того, кто из игроков обладает большей властью или, другими словами, имеет преимущество в переговорной силе. Если такое преимущество имеет первый игрок, то будет решаться задача 1, если таким преимуществом обладает второй игрок, то решаться будет соответственно задача 2. Очевидно, что

Решим задачу 1, т.е.

Имеем задачу нахождения условного экстремума для функции . Для её решения используем функцию Лагранжа.

Найдём частные производные и приравняем их к нулю.

.

Отсюда получаем условие первого порядка (необходимое условие экстремума, касающиеся первых производных)

Исключая параметр получим уравнение:

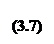
В уравнении (3.7) предельные полезности продуктов обмена для первого игрока

Предельная норма замещения продукта x продуктом y для первого игрока будет в этом случае равна:

.

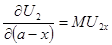
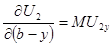
Таким образом, из условия первого порядка следует уравнение:

Следовательно, все точки на контрактной кривой удовлетворяют уравнению (3.8). К уравнению (3.8) нужно добавить условия индивидуальной рациональности:

Решение задачи максимизации полезности вторым игроком (задача 2) будет аналогичным.

Если оба продукта x и y являются нормальными товарами, то можно показать, что в некоторой точке переговорного множества будет выполняться и условие второго порядка. Следовательно, контрактная кривая описывается уравнением (3.8). Переговорное множество удовлетворяет уравнению (3.8) и системе неравенств (3.9).

Пример. Два туземных племени живут охотой и рыболовством. Для того, чтобы природные ресурсы не истощались, правительство установило общие квоты на отлов рыбы и отстрел дичи: рыбы – не более 100 тонн в год; дичи – не более 400 тонн в год.

Первоначально первое племя добывало 60 тонн рыбы и 20 тонн дичи, а второе племя добывало 40 тонн рыбы и 20 тонн дичи.

Предположим, что каждое из племён имеет собственную функцию полезности:

§ где – количество рыбы, а 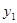– количество дичи;

§ где – количество рыбы, а – количество дичи.

Вожди обоих племён собрались и решили заключить соглашение об охоте и рыболовстве, выполнение которого должно увеличить полезность каждого племени. Требуется найти множество контрактов, улучшающих положение каждого племени, т.е. необходимо найти контрактную кривую.

Решение. Изобразим ящик Эджворта (см. рис.3.)

 

 

Рисунок 3

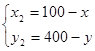
Найдём уравнение контрактной кривой, для чего обратимся к функции (3.8). Найдём предельные нормы замещения:

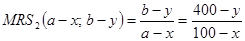
Подставляя в уравнение (3.8), получим

Уравнение (_***) – уравнение контрактной кривой.

Для того, чтобы на контрактной кривой определить переговорное множество, нужно найти полезности каждого племени в точке угрозы:

Найдём полезность каждого племени в точках на контрактной кривой:

.

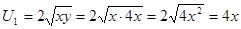
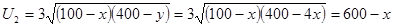Получаем условия индивидуальной рациональности.

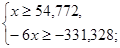
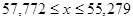
Арбитражное решение

Рассмотрим ящик Эджворта и построим в нём переговорное множество (см. рис. 4).

Рисунок 4

Построим контрактную кривую . Точка T, находящаяся на пересечении двух кривых и , является точкой угрозы. Отрезок на кривой контрактов между точками и представляет собой переговорное множество.

Каждой точке на кривой контрактов соответствует определённые значения полезностей каждого из участников и . Таким образом, каждой точке на кривой контрактов соответствует пара чисел и Всей кривой контрактов соответствует геометрическое множество точек на координатной плоскости (см. рис. 5.).

Рисунок 5

На рис.5. в точке 0 а 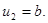На рис. 3.5. этой точке соответствует точка с координатами . В точке на рис. 3.4. а На рис.5 ей соответствует точка с координатами .

Двигаясь из точки в точку , мы будем увеличивать полезность первого игрока и уменьшать полезность второго. Получим кривую AB. Она называется кривой Парето-эффективных решений для данной игры (иногда эту кривую называют множеством Парето-оптимальных решений). Изобразим на рис. 5. точку T₀ , где и – полезности участников в точке угрозы. Условием заключения контракта будут условия индивидуальной рациональности . На рис.5 этим условиям будет соответствовать дуга .

Дуга представляет собой переговорное множество, которое, в свою очередь, является подмножеством множества Парето-эффективных решений, для которого выполняются условия индивидуальной рациональности.

Любая точка на кривой для каждого из участников лучше, чем точка T₀. Переход из любой точки кривой в другую точку этой кривой улучшает положение одного из участников, ухудшая при этом положение другого. Возникает вопрос о существовании какого-либо оптимального компромиссного решение?

Д. Нэш доказал, что существует (при том единственное) решение задачи с торгом, удовлетворяющее следующим критериям:

1. Решение является эффективным (оптимальным) по Парето.

2. Полезность каждого участника при этом решении не меньше, чем в точке угрозы.

3. Решение не изменится, если сумма общего выигрыша будет преобразована по линейному закону где 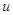– первоначальная сумма общего выигрыша; и 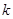– Это свойство называется инвариантностью относительно линейного преобразования.

4. Решение не изменится, если перенумеровать участников игры (свойство симметрии).

5. Независимость от альтернатив, не имеющих отношения к делу. Это значит, что все возможные альтернативы, которые рациональные игроки не будут использовать, можно исключить из рассмотрения.

Нэш доказал, что решением, которое удовлетворяет всем вышеперечисленным критериям, является решение, для которого функция достигает своего максимума на множестве точек переговорного множества[7]. Решение справедливо для любого конечного числа игроков. Если имеются два игрока, то решение Нэша принимает вид:

,

при условии, что .

В чём смысл каждого из пяти критериев решение Нэша?

Первый. Рассмотрим игру с двумя участниками, полезности которых равны и соответственно (см. рис. 6.)

Рисунок 6

 

 

При переходе от A к B полезности обоих участников возрастают. Таким образом, B – Парето-эффективнее, чем A, и C – Парето-эффективнее, чем A. Сравнивая B и C, мы находим, что C – выгоднее, чем B для первого участника, но не выгодно для второго. Это обстоятельство говорит о том, что решения B и C являются несопоставимыми по Парето.

Если альтернативными для участников являются решения A, B и C, то рациональные участники отбросят решение A как Парето-неэффективное и оставят B и C. Очевидно, что оптимальным решением будет либо решение C, либо решение B.

Этот критерий означает, что игроки рассматривают только эффективные по Парето решения.

Второй. Этот критерий соответствует условиям индивидуальной рациональности.

Третий. Предположим, что общую сумму выигрышей двух участников увеличили вдвое. Очевидно, что вдвое увеличится полезность каждого из участников. Требуется ли при этом искать новые решения для этой комбинации? Если пользоваться решением Нэша, то этого делать не нужно. В частности, третий критерий означает, что переход от одной единицы измерения к другой не изменяет решения Нэша. Такие решения Нэша не изменятся, если каждой полезности добавить некоторую константу.

Четвёртый. Решение, найденное для одной нумерации, не изменится при другой нумерации.

Пятый. Если для случая, описанного на рис. 6, ввести четвёртую альтернативу D, то решение не изменится, потому что альтернатива D не будет рассматриваться отдельными игроками.

Решение Нэша называют также арбитражным решением. Это объясняется тем, что, если бы участники игры обратились к независимому арбитру для решения их торгового спора (т.е. для выбоора точки в переговорном множестве), то решение арбитра совпало бы с решением Нэша.

Пример. Пусть вожди племён (см. выше рассмотренный пример) обратились к старейшине (арбитру) для решения их спора. Требуется найти решение, которое примет старейшина.

Решение. Найдём на плоскости множество Парето-оптимальных решений (см. рис.7). Для этого найдём функциональную зависимость между полезностями племён и . Ранее было получено, что на контрактной кривой имеет место система уравнений

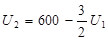
Рисунок 7

 

Арбитражное решение – это такое решение, при котором достигает своего максимума произведение

,

где .

Рассматривая кривую, на которой

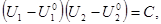где получаем, что 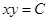– уравнение гиперболы.

Максимизируя произведение (3.10), будем смещать гиперболу вверх и вправо до тех пор, пока она не окажется не границе допустимой области. В этом положении гипербола будет касаться кривой .

Уравнение (3.10) равносильно задаче об отыскании условного экстремума

 

 

Решим эту задачу с помощью функции Лагранжа:

 

 

Решая эту систему, находим решение (единственное). Очевидно, что найденное решение и будет координатами точки касания гиперболы и торгового множества.

Множество решений кооперативной игры называется множеством Парето-оптимальных решений, если:

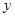1. Для всех решений найдётся такое решение что для первого участника решение будет лучше чем и не хуже чем 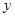для всех остальных участников.

2. Для всех двух решений переход от к улучшает положение хотя бы одного участника и ухудшает положение хотя бы одного другого. Т.е. и являются решениями несравнимыми по Парето.

На рис. 8. изображена область Парето-эффективных решений.

 

Рисунок 8

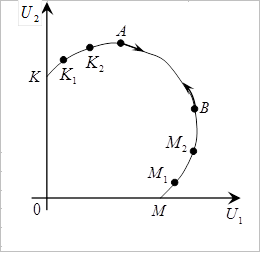
Все ли решения на кривой KM являются Парето-оптимальными? Т.к. а то получается, что область – область Парето-оптимальных решений. Дуга Парето-оптиальных решений всегда имеет отрицательный наклон. Вопрос о её выпуклости и вогнутости не имеет однозначного ответа.

Пример. Если два участника игры решают заключить контракт, т.е. решают предпринимать кооперативные действия, то их обмены будут располагаться на контрактной кривой. Пусть на контрактной кривой полезности участников связаны уравнением .

Решение. Найдём на плоскости множество Парето-оптимальных решений (см. рис.9).

Рисунок 9

 

Пусть при прежних условиях

.

На рис.10 изобразим множество Парето-эффективых решений.

,

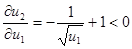
т.е. кривая имеет отрицательный наклон и является вогнутой.

Рисунок 10

 

Для случая, когда в обмене участвуют товары, на которые распространяется закон Госсена (убывание предельной нормы замещения), характерна выпуклая форма Парето-оптимального множества. Эта форма используется в большинстве задач.

ПРАКТИКУМ

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: