 |
Cтатистика предприятий отрасли 3 глава
|
|
|
|
Масштаб статистического графика – это мера перевода числовой величины в графическую.
Масштабная шкала – это линия, отдельные точки которой могут быть прочитаны как числа.
Интервалы между числами могут равными, шкала называется равномерной, и различной величины – неравномерной.
Масштабом равномерной шкалы служит длина отрезка принятого за единицу.
Из неравномерных шкал наиболее широко используются логарифмические.
1.4.5. Классификация видов графиков
Классификация графиков основана на ряде признаков:
а) способ построения графического образа;
б) геометрические знаки, отображающие статистические показатели и их соотношения;
в) задачи, решаемые с помощью графиков.
Выделяют следующие виды классификации
Таблица 1.5.5.1
Классификация статистических графиков по форме графического образа
| Статистические графики по форме графического образа | ||
| линейные | полосовые | объемные |
| статистические кривые | столбиковые полосовые квадратные круговые секторные фигурные точечные фоновые | поверхностные распределения |
Таблица 1.4.5.2
Классификация статистических графиков по способу построения и задачам изображения
| Статистические графики по способу построения и задачам изображения | ||||
| диаграммы | статистические карты | |||
| сравнения | структурные | динамики | картограммы | картодиаграммы |
1.4.6. Статистические диаграммы
Статистические диаграммы подразделяются на: сравнения, структурные и динамики.
Диаграммы сравнения (сопоставления) дают наглядную сравнительную характеристику статистических совокупностей по одному варьирующему признаку.
Диаграммы сравнения:
|
|
|
а) Столбиковые – представляет статистические показатели в виде вертикальных прямоугольников (треугольников, цилиндров, конусов, пирамид …). Каждый столбик выражает величину отдельного уровня ряда.
При построении столбика необходимо начертить систему координат, в которой располагаются столбики. На горизонтальной оси располагаются основания столбика, величина основания произвольная, но одинаковая для всех столбиков.
Шкала, определяющая масштаб столбика по высоте, расположена по вертикальной оси. Таким образом переменной величиной является только одно измерение.
б) Полосовые – разновидность столбиковых (ленточных) диаграмм. Их отличие заключается в том, что масштабная ось расположена горизонтально.
в) Столбиковые и полосовые диаграммы взаимозаменяемые. Их разновидностью являются двусторонне направленные диаграммы.
г) Если в диаграмме сравниваемые величины изображаются в виде правильных геометрических фигур (квадратов, кругов, прямоугольников), площади которых соотносятся между собой как количества, то они называются по форме используемой фигуры. При построении этих диаграмм необходимо из величины признака извлечь квадратный корень (площадь квадрата – сторона в квадрате, площадь круга – радиус в квадрате). Фигуры необходимо располагать на равном расстоянии друг от друга или внутри друг друга с указанием в каждой фигуре числового значения.
Графики Варзара строятся в то случае, если на графике изображаются три взаимосвязанных признака. График представляет собой прямоугольник, каждое измерение которого экономическая величина (длина, ширина и площадь).
д) Фигурные диаграммы являются наиболее наглядными и изображают статистические данные при помощи фигур-знаков, воспроизводящих образ анализируемых предметов.
При построении этих графиков выбирают одну фигуру за масштаб, а величину признака изображают необходимым количеством фигур или их частей.
|
|
|
Структурные диаграммы представляют статистическую совокупность соотношением ее частей в абсолютном и относительном выражении. По внешнему виду подразделяются на прямоугольные, секторные, объемные.
Диаграммы динамики строятся для анализа развития явления во времени. Для графического изображения рядов динамики используют: столбиковые, ленточные, круговые, линейные, радиальные ….
Линейные диаграммы строятся на системе прямоугольных координат. По оси абсцисс – откладывают время, по оси ординат – размеры явлений (размеры признаков). На оси ординат наносят масштабы (равномерные, полулогарифмические). На оси абсцисс промежутки между одинаковыми датами должны быть равны.
Радиальные диаграммы сроятся в полярных координатах. Она разделяются на замкнутые и спиральные и характеризуют циклически развивающиеся явления. В качестве центра отсчета выбирается центр круга или окружность
1.4.7. Статистические карты
Статистические карты представляют собой вид графических изображении статистических данных на схеме географической карты. Они характеризуют степень распространения явления на определенной территории.
Картограмма – это географическая карта, на которой штриховкой, точками или окраской разной насыщенности показывается интенсивность данного показателя на определенной территории.
Картограмма фоновая – вид картограммы, при которой признак обозначается различной интенсивности штриховкой или различной насыщенностью цвета.
Картограмма точечная – вид картограммы, при которой уровень признака изображается величиной тчек, по заранее выбранному масштабу.
Картодиаграмма – это сочетание диаграмм с географической картой.
1.5 АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ
Вопросы
1.5.1. Формы выражения и виды статистических показателей
1.5.2. Абсолютные показатели
1.5.3. Относительные показатели
1.5.1. Формы выражения и виды статистических
показателей
Статистическое исследование обычно заканчивается расчетом показателя или системы показателей. Показатели подразделяются на следующие виды:
Конкретный статистический показатель характеризует величину признака в конкретное время и данном месте.
|
|
|
Показатель-категория характеризует сущность явления без привязки его к месту и времени.
Индивидуальные показатели характеризуют отдельные единицы явления.
Сводные показатели характеризуют часть совокупности или группу единиц.
Расчетные показатели определяются путем вычислений по формулам.
Показатели определенные на конкретную дату называются моментным и, за промежуток времени интервальными.
В зависимости от принадлежности к одному или нескольким объектам, показатели называются одно объектные и меж объектные.
В зависимости от территории, для которой показатели определяются, они подразделяются на обще территориальные, региональные и местные.
1.5.2. Абсолютные показатели
Абсолютные показатели являются первичной формой статистических показателей. Они подразделяются на индивидуальные и общие.
Индивидуальные абсолютн ые показатели получаются в результате статистического наблюдения путем подсчета, измерения.
Общие (сводные) объемные показатели получают в результате сводки и группировки статистических данных и представляют собой общую величину всего объекта или его части.
Абсолютные показатели являются именованными величинами. Они измеряются в следующих единицах измерения:
1. Натуральные единицы измерения – выражают признак в физических мерах (кг., тонны, метры).
2. Условно-натуральные единицы применяются в том случае, если необходимо свести в единый итог разнородную продукцию, имеющую одинаковые потребительные свойства.
Для перевода в условно-натуральные единицы используется коэффициент пересчета
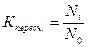 ,
,
где  – технический параметр каждого изделия;
– технический параметр каждого изделия;
 – технический параметр изделия принятого за базу сравнения.
– технический параметр изделия принятого за базу сравнения.
3. Стоимостные абсолютные показатели – дают денежную оценку явлению:
а) абсолютные показатели в расчетных билетах –
РБНЦБ РБ; РБЦБ РФ.
б) абсолютные показатели в валюте (евро, доллар).
4. Трудовые единицы измерения абсолютных величин позволяют учитывать как трудоемкость отдельных видов продукции так и трудоемкость объема всего выпуска продукции.
|
|
|
5. Комбинированные абсолютные показатели – содержат в единицах измерения несколько наименований абсолютных величин (кВт-час; человеко-час)
1.5.3. Относительные показатели
Относительные величины определяются соотношением двух абсолютных величин.
Измеряются относительные величины в локальных единицах (без размерных), в процентах, промилле, про промилле и так далее.
Статистика выделяет следующие виды относительных величин:
планового задания (ОВПЗ);
выполнения плана (ОВВП);
динамики (ОВД);
структуры (ОВСтр;
координации (ОВК);
сравнения (ОВСр);
интенсивности развития (ОВИР).
Рассмотрим определение относительных величин на примере.
Относительная величина планового задания (ОВПЗ ) определяется отношением плановой величины признака в отчетном периоде к его фактической величине в базисном периоде
 .
.
Относительная величина выполнения плана (ОВВП) определяется отношением фактической величины признака к его плановой величине в анализируемом периоде
 .
.
Относительная величина динамики (ОВД) определяется отношением фактического (планового) уровня данного периода к фактическому (плановому) уровню базисного периода.
 .
.
Между этими тремя показателями существует взаимосвязь
ОВД = ОВПЗ ∙ ОВВП.
Относительная величина структуры (ОВСтр ) определяется отношением частей целого к общему итогу
 .
.
Относительная величина координации (ОВК)определяется соотношением между частями единого целого.
Относительная величина сравнения (ОВСр) определяется соотношением
1. двух одинаковых признаков,
2. принадлежащих к разным объектам
3. в одном периоде времени.
Относительная величина интенсивности развития (ОВИР) определяется соотношением
1. различных признаков,
2. принадлежащих одному объекту
3. в одном периоде времени.
Она показывает степень распространения одного признака в другом. Единицы измерения ОВИР состоят из единиц измерения тех абсолютных величин, которые используются в определении относительной величины.
1.6 РЯДЫ РАСПРЕДЕЛЕНИЯ И ИХ ПОКАЗАТЕЛИ
Вопросы
1.6.1. Графическое изображение рядов распределения.
1.6.2. Плотность распределения.
1.6.3. Виды средних величин
1.6.4. Средняя арифметическая величина и ее основные свойства
1.6.5. Показатели колеблемости (вариации) признаков.
1.6.6. Дисперсия и ее свойства.
1.6.7. Правило сложения дисперсий.
1.6.1.Графическое изображение рядов распределения.
К рядам распределения относятся ряды, у которых признак выражен числом. Ряды распределения подразделяются на дискретные и интервальные.
|
|
|
Дискретные ряды распределения могут изображаться при помощи перпендикуляров, кумуляты, полигона частот.
При помощи перпендикуляров – перпендикуляр строится на оси «х» по частоте признака. Частота признака является высотой перпендикуляра, построенного из значения признака на оси «х».
По кумулятивным частотам – построение происходит между признаком «х» горизонтальной оси и кумулятивной частотой вертикальной оси.
Полигон частот – строится как точка пересечения признака «х» на горизонтальной оси и частоты признака на вертикальной оси.
Интервальные ряды динамики могут изображаться при помощи гистограммы, кумуляты, полигонов частот.
При помощи гистограммы
При помощи кумулятивных частот – точка пересечения признака «х» по верхней границе в группировке и накопленной частоте
Полигон частот – точка пересечения признака «х» по середине интервала и частоте признака
1.6.2. Плотность распределения
Плотность распределения определяется для интервальных рядов распределения и подразделяется на абсолютную и относительную.
Абсолютная плотность распределения определяется отношением частоты признака к величине интервала

Относительная плотность распределения определяется отношением частости к величине интервала

1.6.3. Виды средних величин
Один из самых эффективных способов оценить сложившуюся ситуацию заключается в обобщении, то есть использование одного или нескольких отобранных или рассчитанных значений для характеристики набора данных. Подобное изучение каждого отдельного случая не является статистической деятельностью, но обнаружение и идентификация особенностей, которые в целом характерны для рассматриваемых случаев, представляют собой статистическую деятельность, так как вся информация при этом рассматривается в едином целом.
Одна из целей статистики состоит в том, чтобы свести набор данных к одному числу (или нескольким числам), которое выражает фундаментальные свойства данных рядов.
Методы, наиболее подходящие для анализа совокупности, включают определение следующих групп показателей:
1) простые средние;
2) степенные средние.
К простым средним относятся: мода, медиана и средняя хронологическая.
а) Мода – это варианта с наибольшей частотой.
Для дискретных рядов мода определяется визуально
Если в ряду несколько признаков имеют одинаковые наибольшие частоты, то ряд называется би – модальным.
В интервальных рядах распределения мода определяется по формуле
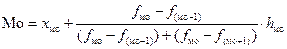 ,
,
где  – частота модального интервала, т. е. интервала содержащего наибольшее число вариант (наибольшую частоту);
– частота модального интервала, т. е. интервала содержащего наибольшее число вариант (наибольшую частоту);
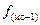 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;
 – частота интервала, следующего за модальным;
– частота интервала, следующего за модальным;
 – длина модального интервала;
– длина модального интервала;
 – нижняя граница модального интервала.
– нижняя граница модального интервала.
Модальным интервалом является интервал «10 – 15», так как его частота 22 самая большая в ряду.

Мода определяется графически по гистограмме. Для этого выбирается самый высокий прямоугольник, его вершины крест на крест соединяются с вершинами соседних прямоугольников. Из точки пересечения опускается перпендикуляр на ось «х». Точка пересечения перпендикуляра и оси показывает значение моды.
б) Медиана – соответствует варианте, стоящей в середине ранжированного (упорядоченного) ряда.
Для дискретных рядов.
Положение медианы определяется ее номером:
 ,
,
где n – объем ряда.
Определяем значение медианы по примеру
Для определения медианы в интервальном ряду воспользуемся формулой
 ,
,
где  – кумулятивная (накопленная) частота интервала, предшествующего медианному;
– кумулятивная (накопленная) частота интервала, предшествующего медианному;
 – нижняя граница медианного интервала;
– нижняя граница медианного интервала;
 – частота медианного интервала;
– частота медианного интервала;
 – длина медианного интервала.
– длина медианного интервала.
Медианный интервал – первый интервал, накопленная частота которого превышает половину суммы частот.
Медиана может определятся графически по кумуляте.
На графике кумуляты проводится горизонтальная линия с координатами  ; х – каждое значение признака. Из точки пересечения данной линии с графиком кумуляты опускается перпендикуляр на ось «х». В точке пересечения перпендикуляра и оси будет медиана.
; х – каждое значение признака. Из точки пересечения данной линии с графиком кумуляты опускается перпендикуляр на ось «х». В точке пересечения перпендикуляра и оси будет медиана.
г) Средняя хронологическая величина определяется по формуле
 .
.
Средняя применяется в том случае, если признаки отстоят друг от друга по времени на равные даты.

2 ) Степенные средние определяются по формуле
 ,
,
где m – показатель степени.
В зависимости от показателя степени «m» образуются различные виды степенных средних:
при m = 1, получаем среднюю арифметическую

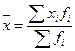 ;
;
при m = 2, получаем среднюю квадратическую
 ;
;
при m = 3, получаем среднюю кубическую
 ;
;
при m = 0, получаем среднюю геометрическую
 ;
;
при m = –1, получаем среднюю хронологическую
 .
.
1.6.4. Средняя арифметическая и ее основные
свойства
Наиболее широко из средних величин в экономике используется средняя арифметическая величина.
Определение средних величин для дискретных и интервальных рядов имеет особенность. В дискретных рядах признак берётся сам по себе а в интервальных – заменяется серединой интервала.
Для не сгруппированных данных средняя арифметическая определяется по формуле
 ,
,
где n – число элементов в совокупности;
хi – непосредственно сами данные (варианты).
Для сгруппированных данных средняя арифметическая определяется по формуле
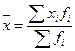 ,
,
где fi – частота интервала.
Средняя арифметическая обладает рядом свойст.
1) Произведение средней арифметической на сумму частот равно сумме произведений вариантов на соответствующие им частоты
 .
.
2) Сумма отклонений индивидуальных значений признака от средней арифметической равно нулю
 .
.
3) Если каждую варианту уменьшить или увеличить на постоянное число «А», то средняя арифметическая уменьшится или увеличится на это число

4) Если каждую варианту уменьшить или увеличить в постоянное число «С» раз, то средняя арифметическая уменьшится или увеличится в это число раз

 .
.
5) Если все частоты уменьшить или увеличить в «К» раз, то средняя арифметическая не изменится
 .
.
Метод определения средней арифметической с использованием свойств, называется методом моментов.
1.6.5. Показатели вариации признаков.
Для характеристики надежности средней арифметической определяются показатели вариации.
К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
Размах вариации признака определяется по формуле
R = х макс– х мин,
где х макс – максимальное значение признака;
х мин – минимальное значение признака.
Среднее линейное отклонение признака от средней арифметической определяется по формуле
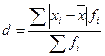 .
.
Дисперсия количественного признака определяется по формуле
 , или
, или  .
.
Дисперсия качественного признака определяется по формуле

где w – удельный вес признака.
Среднеквадратическое отклонение признака определяется по формуле
 .
.
К относительным показателям вариации относят коэффициент осцилляции, относительное линейное отклонение и коэффициент вариации. Все они вычисляются как отношение абсолютных показателей вариации к средней арифметической и используются для сравнения различных признаков одной и той же совокупности, или же при сравнении колеблемости одного и того же признака в различных совокупностей.
Коэффициент осцилляции определяется по формуле

Коэффициент вариации по линейному отклонению (относительное линейное отклонение) определяется по формуле

Коэффициент вариации по среднему квадратическому отклонению определяется по формуле
 .
.
Если значение этого показателя меньше 34%, то ряд распределения равномерен.
1.6.6. Дисперсия и ее свойства.
Дисперсия определяется по формулам
 ;
;  .
.
Она обладает рядом свойств:
1 Дисперсия постоянной величины равна нулю.
2 Если уменьшить или увеличить все значения признака на постоянное число «А», то дисперсия не изменится

 .
.
3 Если уменьшить или увеличить все значения признака в постоянное число «С», то дисперсия уменьшится или увеличится в квадрат этого числа раз
 ;
;  .
.
4 Дисперсия от любой величины «В» всегда будет больше дисперсии от средней арифметической.
 >
>  .
.
Среднее квадратическое отклонение – это корень квадратный из дисперсии
 .
.
В условиях нормального распределения существует зависимость между его величиной и числом наблюдений:
в пределах  – находится 68,3 % количества наблюдений;
– находится 68,3 % количества наблюдений;
в пределах  – находится 95,4 % количества наблюдений;
– находится 95,4 % количества наблюдений;
в пределах  – находится 99,7 % количества наблюдений.
– находится 99,7 % количества наблюдений.
На практике, обычно, отклонения не превышают  . Это положение называют правилом трех сигм.
. Это положение называют правилом трех сигм.
1.6.7. Правило сложения дисперсий.
Если необходимо определить дисперсию для нескольких рядов, то можно воспользоваться формулой сложения дисперсий

где  – межгрупповая дисперсия определяется по формуле
– межгрупповая дисперсия определяется по формуле
 ,
,
где 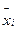 – средняя арифметическая в каждой группе;
– средняя арифметическая в каждой группе;
n – количество признаков в группе;
 – общая средняя определяется по формуле
– общая средняя определяется по формуле
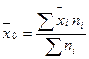 ;
;
 – средняя из внутри групповых дисперсий определяется по формуле
– средняя из внутри групповых дисперсий определяется по формуле
 ;
;
 –внутригрупповая дисперсия определяется по формуле
–внутригрупповая дисперсия определяется по формуле
 .
.
1.7ХАРАКТЕРИСТИКА ФОРМЫ РАСПРЕДЕЛЕНИЯ
Вопросы
1.7.1. Начальные и центральные моменты распределения.
1.7.2. Показатели асимметрии и эксцесса.
1.7.3. Построение кривой нормального распределения.
1.7.1. Начальные и центральные моменты
распределения.
Средняя арифметическая и дисперсия являются частными случаями более широкого понятия о моментах распределения. Различают начальные и центральные эмпирические моменты распределения.
Начальным эмпирическим моментом «q» порядка называется средняя арифметическая взвешенная «q» степеней признака

Начальный эмпирический момент
|
|
|


