 |
Задание на лабораторную работу
|
|
|
|
На основании данных вариантов табл. 3.3, 3.4, определить все возможные относительные величины для каждого предприятия.
Результаты представить в таблице.
Порядок выполнения отчета
1. Для начала работы необходимо открыть лабораторную работу в папке «Статистика предприятия» под названием «Лаб. № 3 Относительные величины».
2. Скопируйте данные варианта с листа «Исх. данные» на лист «Свой вариант».
3. В соответствии с вариантом табл. 3.3 составить таблицу исходных данных табл. 3.4.
4. Определить все возможные относительные величины.
5. Представить результаты в таблице.
6. Сделать выводы.
Содержание отчета
Титульный лист.
Название и цель работы.
Таблица исходных данных.
Таблица с расчетами относительных величин.
Выводы по работе.
Контрольные вопросы
1. Назовите виды относительных величин.
2. По каким формулам определяются относительные величины?
3. В каких единицах измерения определяются относительные величины всех видов?
Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 4
ПОКАЗАТЕЛИ ВАРИАЦИИ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ ВЕЛИЧИНЫ
Цель лабораторной работы: изучить виды средних величин, приобрести опыт определения показателей вариации.
Теоретические положения
Одним из самых эффективных способов оценить сложившуюся ситуацию заключается в обобщении, то есть использовании одного или нескольких отобранных или рассчитанных значений для характеристики набора данных. Подобное изучение каждого отдельного случая не является статистической деятельностью, но обнаружение и идентификация особенностей, которые в целом характерны для рассматриваемых случаев, представляют собой статистическую деятельность, так как вся информация при этом рассматривается в едином целом.
|
|
|
Одна из целей статистики состоит в том, чтобы свести набор данных к одному числу (или нескольким числам), которое выражает фундаментальные свойства данных. Методы наиболее подходящие для анализа совокупности включают определение следующих показателей.
Среднее, медиана, мода – это различные способы выбора единственного числа, которое лучше всего описывает исследуемую совокупность.
Определение средних величин для дискретных и интервальных рядов имеет особенности. В дискретных рядах признак берётся сам по себе, в интервальных – заменяется серединой интервала.
Пример. Определить среднюю арифметическую, моду, медиану, показатели вариации средней арифметической величины на основании данных табл. 4.1 для дискретных рядов, табл. 4.2 для интервальных рядов.
Решение для дискретных рядов.
Таблица 4.1
Группы по разряду работ
| Величина разряда, хi | Частота, fi | Частость, Wi % | Накопленные частости, S % | хi fi |
| 6,7 | 6,7 | |||
| 13,3 | 20,0 | |||
| 20,0 | 40,0 | |||
| 33,3 | 73,3 | |||
| 16,7 | 90,0 | |||
| 10,0 | 100,0 | |||
| ∑ | 100,0 | – |
Среднее значение признака, рассчитывается по формуле средней арифметической «
».
Для несгруппированных данных средняя определяется
,
где n – число элементов в совокупности;
хi – непосредственно сами данные (варианты).
Для сгруппированных данных средняя
,
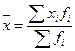где fi – частота интервала.
Так как данные признака в примере сгруппированны, то расчет средней арифметической осуществляется по формуле средней арифметической взвешанной:
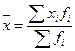
(разряд).
Медиана соответствует варианте, стоящей в середине ранжированного (упорядоченного) ряда. Положение медианы определяется ее номером:
.
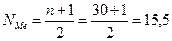Так как данная совокупность содержит четное число элементов, то значение медианы определяют по формуле
|
|
|
,
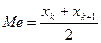где хк и хк+1 –варианты, находящиеся в центре совокупности (в примере варианты под номером 15 и 16).
(разряд).
Мода – это варианта с наибольшей частотой (f макс = 10)
Мо = 4 (разряд).
Решение для интервальных рядов.
Так как данные признака в примере сгруппированны, то расчет средней арифметической осуществляется по формуле
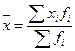
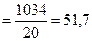млн руб.
Таблица 4.2
Распределение предприятий по уровню затрат
| № п/п | Группы предприятий по величине затрат, млн руб. | Число Предприятий, fi | Накопленная частота,
| Середина интервала, хi |
| 30–38 | ||||
| 38–46 | ||||
| 46–54 | ||||
| 54–62 | ||||
| 62–70 | ||||
| ∑ | – | – | – |
В интервальных рядах распределения мода определяется по формуле
,
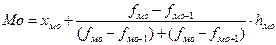где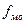 
– частота модального интервала, т. е. интервала содержащего наибольшее число вариант;
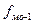– частота интервала, предшествующего модальному;
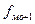– частота интервала, следующего за модальным;
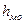– длина модального интервала;
– нижняя граница модального интервала.
млн руб.
Для определения медианы в интервальном ряду воспользуемся формулой
,
где 
– кумулятивная (накопленная) частота интервала, предшествующего медианному;
– нижняя граница медианного интервала;
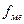– частота медианного интервала;
– длина медианного интервала.
Медианный интервал – первый интервал, накопленная частота которого превышает половину суммы частот.
В данном примере всего предприятий 20, следовательно, половина частот 20 / 2 = 10 и первый интервал, накопленная частота которого больше 10 это 54–62 (см. табл. 3.2, в четвертом интервале накопленная частота ровна 17, что больше 10).
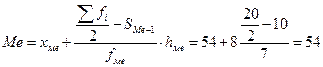млн руб.
К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
Размах вариации признака определяется по формуле
R = х макс– х мин,
где х макс – максимальное значение признака;
х мин – минимальное значение признака.
R = 70 – 30 = 40 млн руб.
или
R = 64 – 34 = 30 млн руб.
Для расчета показателей ряда распределения удобно воспользоваться табл. 4.3.
|
|
|
Таблица 4.3
Расчет показателей вариации
| № п/п | Середина интервала | Число предприятий | x f | │ х – │ f
| 
|
| 53,10 | 939,87 | ||||
| 19,40 | 188,18 | ||||
| 8,50 | 14,45 | ||||
| 44,10 | 277,83 | ||||
| 36,92 | 453,87 | ||||
| ∑ | – | 162,00 | 1874,20 |
Среднее линейное отклонение признака от средней арифметической определяется по формуле
, 
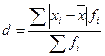млн руб.
Дисперсия признака определяется по формуле
σ2 х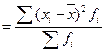 
, σ2 х 
.
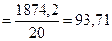Среднее квадратическое отклонение признака определяется по формуле
σ х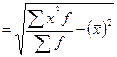 
млн руб.
К относительным показателям вариации относят коэффициент осцилляции, относительное линейное отклонение и коэффициент вариации. Все они вычисляются как отношение абсолютных показателей вариации к средней арифметической и используются для сравнения различных признаков одной и той же совокупности или же при сравнении колеблемости одного и того же признака в различных совокупностей.
Коэффициент осцилляции определяется по формуле
К(R) = R / ∙ 100 % = 40 / 51,7 ∙ 100 % = 77,4 %.
Коэффициент вариации по линейному отклонению (относительное линейное отклонение определяется по формуле
К(d) = d / ∙ 100 % = 8,1 / 51,7 ∙ 100 % = 15,7 %.
Коэффициент вариации по среднему квадратическому отклонению определяется по формуле
V = σ х / ∙ 100 % = 8,1 / 51,7 ∙ 100 % = 18,72 %.
Значение коэффициента вариации меньше 33 %, что свидетельствует об однородности совокупности.
Величина затрат по предприятиям отличается от среднего уровня 51,7 млн руб. на 18,72 %.
|
|
|
