 |
Задание на лабораторную работу
|
|
|
|
Провести анализ рядов распределения по признакам «х» и «у» на основании данных лабораторной работы № 2 «Группировка статистических данных табл. 2.2, 2.3.
Порядок выполнения работы
1. Найдите лабораторную работу в папке «Статистика предприятия» под названием «Лаб. № 4 Показатели вариации средней арифметической величины».
2. На основании группировок по признакам «х» и «у» лабораторной работы № 2 построить графики рядов распределения: перпендикуляры, гистограммы, полигоны, кумуляты.
3. Определить средние уровни рядов: средние арифметические, моды, медианы; аналитическим и графическим путем.
4. Определить показатели вариации рядов распределения: размах вариации, среднее квадратическое отклонение, среднее линейное отклонение, коэффициенты осцилляции, вариации по среднему линейному отклонению; по среднему квадратическому отклонению.
5. Сделать выводы.
Содержание отчета
Титульный лист.
Название и цель работы.
Таблицы исходных данных.
Расчет показателей аналитическим и графическим путем.
Выводы по работе.
Контрольные вопросы
1. Виды средних величин.
2. Формулы определения простых средних.
3. Методы определения степенной средней.
4. Показатели вариации средней арифметической.
Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 5
ХАРАКТЕРИСТИКА ФОРМЫ РАСПРЕДЕЛЕНИЯ
Цель лабораторной работы: приобрести практический опыт анализа кривой нормального распределения.
Теоретические положения
Наиболее распространенными для анализа кривой нормального распределения являются показатели асимметрии и эксцесса.
Асимметрия характеризует симметричность кривой нормального распределения относительно средней арифметической и рассчитывается по формуле
|
|
|
,
где µ 
– центральный момент третьего порядка, который определяется по формуле
.
Показатель эксцесса отражает форму вершины кривой нормального распределения и рассчитывается по формуле
где µ 
– центральный момент четвертого порядка, который определяется по формуле
.
Для расчета асимметрии и эксцесса удобно воспользоваться расчетной табл. 5.1.
Таблица 5.1
Расчет асимметрии и эксцесса
| f | 
| 
| 
| 
| 
|
| –3 | –9 | –34,172 | 76,887 | |||
| –2 | –4 | –3,910 | 4,883 | |||
| –5 | –5 | –0,078 | 0,0195 | |||
| 2,953 | 2,215 | |||||
| +1 | 16,078 | 28,137 | ||||
| ∑ | – | –15 | –19,128 | 112,1415 |
Центральные моменты определяем для простаты расчета по условным значениям признака «х».
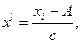
где A = 58, так как у признака 
самая большая частота;
с = 8, так как c = h = 8.
– 0,75.
Средняя арифметическая действительная определяется по формуле момента
– 0,75 ∙ 8 + 58 = 52 млн руб.
Среднее квадратическое отклонение условное определяется по формуле
;
.
Действительное значение среднего квадратического отклонения определяется умножением условного на «с».
σ х = σ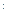 
х ∙ с= 1,26 ∙ 8 = 10, 08 млн руб.;
– 0,478.
Т.к. асимметрия < 0, то кривая имеет левостороннюю асимметрию по отношению к средней арифметической.
Оценка существенности асимметрии проводится с помощью средней квадратической ошибки.
σ Аs 
,
где n – число наблюдений.
σ Аs 
= 0,4858.
Так как отношение коэффициента асимметрии по модулю к средней квадратической ошибке меньше 3, то асимметрия не существенна, и ее наличие обусловливается влиянием случайных факторов (0,478 / 0,4858 = 0,986 < 3).
;
0,775.
Так как 
– 0,775 < 0, то вершина плотности распределения является плоской.
|
|
|
Строим график эмпирических частот и проверяем гипотезу об их соответствии кривой нормального распределения.
Для проверки гипотезы необходимо определить теоретические частоты по формуле плотности нормального распределения
.
Для удобства расчета теоретических частот обозначим:
через коэффициент доверия – 
;
через функцию – 
.
Расчет теоретических частот удобно проводить в табл. 5.2.
Таблица 5.2
Расчет теоретических частот
|
|
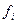
| t | φ | f теор | 
|
| –1,785714 | 0,081213 | 0,50 | |||
| –0,992063 | 0,244538 | 1,00 | |||
| –0,198413 | 0,0392203 | 0,17 | |||
| 0,595238 | 0,335060 | 0,17 | |||
| 1,388889 | 0,152469 | 0,50 | |||
| – | – | 2,34 |
Теоретические частотыисходя из функции плотности распределения определяются по формуле
,
где 
– постоянная часть.
= 
.
Если суммы теоретических и эмпирических частот равны, то расчеты выполнены верно. Наносим теоретические частоты на график эмпирических частот.
Для характеристики состоятельности гипотезы о принадлежности кривой типу кривых нормального распределения определяем критерий ХИ – квадрат «
» по формуле
Расчетное значение критерия сравнивается с табличным, если оно меньше или равно табличному значению, значит, гипотеза о принадлежности кривой нормальному распределению верна.
Вывод. 
= 2,34, следовательно гипотеза о кривой нормального распределения с вероятностью 0,99 верна, так как табличное значение (табл. 5.3) 
= 7,63.
Таблица 5.3
Табличное значение ХИ – квадрат для 20 пар признаков
| Р | 0,99 | 0,98 | 0,90 | 0,80 | 0,70 | 0,50 | 0,30 | 0,20 | 0,1 |
|
| 7,63 | 8,57 | 10,1 | 11,7 | 13,7 | 15,4 | 18,3 | 21,7 |
Примечание: Р –вероятность в коэффициентах, с которой определяют табличное значение.
|
|
|
