 |
Задание на лабораторную работу
|
|
|
|
Проверить соответствие кривых типу кривых нормального распределения, определив их асимметрии и эксцесс.
Порядок выполнения работы
1. Для начала работы необходимо открыть лабораторную работу в папке «Статистика предприятия» под названием «Лаб. № 5 Характеристика формы распределения».
2. Определить коэффициенты асимметрии и эксцесса по признакам «х» и «у» лабораторной работы № 2 табл. 2.2, 2.3.
3. Рассчитать теоретические частоты.
4. Построить график эмпирических и теоретических частот.
5. Рассчитать критерий ХИ – квадрат.
6. Сделать выводы на основании коэффициентов асимметрии, эксцесса и критерия ХИ – квадрата.
Содержание отчета
Титульный лист.
Название и цель лабораторной работы.
Табл. 2.2, 2.3 исходных данных по признакам «х» и «у» из лабораторной работы № 2.
Таблицы для расчетов коэффициентов асимметрии и эксцесса.
Таблица расчета теоретических частот (см. табл. 5.2).
Графики теоретических и эмпирических частот.
Выводы по работе.
Контрольные вопросы
1. Виды форм распределения.
2. Симметричное и асимметричное распределение.
3. Показатель формы вершины кривой нормального распределения и его характеристики.
4. Формула определения теоретических частот.
5. Критерий ХИ – квадрат и его анализ.
Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 6
ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ МЕЖДУ ЯВЛЕНИЯМИ
Цель лабораторной работы: получить практические навыки в изучении взаимосвязи между двумя признаками.
Теоретические положения
Исследование объективно существующих взаимосвязей между явления – важнейшая задача общей теории статистики. В процессе изучения взаимосвязей вскрываются причинно-следственные отношения между явлениями, что позволяет выявить факторы, оказывающие наибольшее влияние на вариации изучаемых явлений и процессов. Регрессионный анализ позволяет осуществлять прогнозирование будущих результатов.
|
|
|
Пример. На основании приведенных данных в табл. 6.1 провести исследование взаимосвязи между признаками, «у» – результативный признак, «х» – факторный. Определить аналитическое выражение связи и проверить его на достоверность.
Таблица 6.1
Исходные данные для изучения зависимости
| х | 5,3 | 7,3 | 8,2 | 13,8 | 14,4 | 18,7 | 24,9 | 25,3 | 25,7 | |
| у | 67,6 | 66,6 | 63,5 | 60,4 | 59,4 | 56,9 | 53,6 | 52,5 |
Решение. Первичная информация проверяется на однородность признака по коэффициенту вариации.
V = σ х / 
∙ 100 % = 7,81 / 17,5 ∙ 100 % = 44,6 %.
Так как коэффициент вариации больше 34 %, то признаки не однородны в своих рядах.
Для измерения тесноты связи при прямолинейной зависимости используется коэффициент корреляции ( 
), значения параметров для его расчета определены в табл. 6.2.
.
Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы. (–1 ≤ r ≤ +1). Минус показывает на наличие обратной связи между признаками. Если коэффициент равен единице по модулю, то связь функциональная, если по модулю больше 0,5, то связь сильная. Следовательно, связь между признаками сильная (тесная), обратная, так как коэффициент корреляции по модулю близок к единице и отрицательный.
; 
; 
;
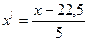= – 1,6 ∙ 5 + 25,5 = 17,5;
σ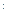 
х 
;
σ х = 5 ∙ 1,56 = 7,81;
; 
;
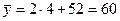σ 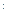х 
; σ х = 4 × 1,61 = 4,45;
;
; 
;
b = – 0,984; а = 0,426; 
;
; 
.
Для оценки тесноты связи при криволинейной зависимости применяется корреляционное отношение (η)
η = 
,
где 
.
Корреляционное отношение изменяется в тех же пределах, что и коэффициент корреляции. Следовательно криволинейная зависимость между признаками отсутствует, так как корреляционное отношение меньше 0,5.
|
|
|
Таблица 6.2
Вспомогательная таблица для расчета
| у | 50–54 | 54–58 | 58–62 | 62–66 | 66–70 | 
| 
| 
| 
| ||
| х | 
| ||||||||||
| 
| ||||||||||
| 3–8 | 5,5 | –4 | –8 | –32 | |||||||
| 8–13 | 10,5 | –3 | –3 | –12 | |||||||
| 13–18 | 15,5 | –2 | –4 | –10 | |||||||
| 18–23 | 20,5 | –1 | –1 | –2 | |||||||
| 23–28 | 25,5 | ||||||||||
| –16 | –56 | |||||||||
| |||||||||||
|
Задание на лабораторную работу
Провести корреляционный анализ ряда распределения и выявить наличие связи между признаками «х» и «у».
Порядок выполнения работы
1. Для начала работы необходимо открыть лабораторную работу в папке «Статистика предприятия» под названием «Лаб. № 6 Изучение взаимосвязи между явлениями».
2. На основании корреляционной табл. 2.4 лаб. № 2 провести исследование взаимосвязи между признаками, «y» – результативный признак, «x» – факторный признак, предложив два вида корреляционной зависимости.
3. Найти аналитическое выражение связи и проверить на достоверность.
4. Построить графики теоретических и эмпирических значений признаков.
5. Сделать выводы.
Содержание отчета
Титульный лист.
Корреляционная таблица с исходными данными.
График эмпирических и теоретических частот.
Таблицы с расчетами параметров уравнений.
Расчеты тесноты связи между признаками.
Выводы по работе.
Контрольные вопросы
1. Виды корреляционных зависимостей.
2. Выбор вида зависимости.
3. Показатели тесноты связи.
Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 7
РЯДЫ ДИНАМИКИ
Цель лабораторной работ: приобретение навыков в определение показателей ряда динамики.
Теоретические положения
Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, т.е. их динамика. Эта задача решается при помощи анализа рядов динамики (или временных рядов).
|
|
|
Ряд динамики представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени.
Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития общественного явления во времени. Эти закономерности не проявляются четко на каждом конкретном уровне, а лишь в тенденции, в длительной динамике.
Пример. По данным табл. 7.1 рассчитайте базисные и цепные: абсолютные приросты; темп роста и темп прироста; абсолютное значение одного процента прироста; средний уровень ряда; средний абсолютный прирост; средний темп роста; средний темп прироста.
Таблица 7.1
Выпуск продукции
| Месяц | Выпуск в млн руб. | Месяц | Выпуск в млн руб. |
| Январь | 7,3 | Март | 12,8 |
| Февраль | 9,5 | Апрель | 12,0 |
Решение. Абсолютный прирост (Dy) характеризует увеличение или уменьшение уровня ряда за определенный промежуток времени и рассчитывается цепным или базисным способом.
Абсолютный прирост цепной рассчитывается как разница между последующими и предыдущими значениями
D y ц = yi – yi-1,
где yi – уровень сравниваемого периода;
yi-1 – уровень предшествующего периода.
D y цфевр/янв = 9,5 – 7,3 = + 2,2 млн руб;
D y цмарт/февр = 12,8 – 9,5 = + 3,3 млн руб;
D y цапр/март = 12,0 – 12,8 = – 0,8 млн руб.
Абсолютный прирост базисный рассчитывается как разница между текущим значением ряда и базисным значением
D y б = yi – y0,
где y0 – уровень базисного периода.
D y бфевр/янв = 9,5 – 7,3 = +2,2 млн руб;
D y бмарт/янв = 12,8 – 7,3 = +5,5 млн руб;
D y бапр/янв = 12,0 – 7,3 = + 4,7 млн руб.
Для оценки относительного изменения уровня ряда динамики за определенный период времени вычисляют темпы роста и прироста, как цепным, так и базисным способом.
Темп роста цепной рассчитывается как отношение последующего значения к предыдущему
100 %;
Т цр.февр/ янв = 9,5 / 7,3 ∙ 100 % = 130,14 %;
Т цр.март/февр = 12,8 / 9,5 ∙ 100 % = 134,74 %;
Т цр.апр/март = 12,0 / 12,8 ∙ 100 % = 93,75 %.
|
|
|
Темп роста базисный рассчитывается как отношение каждого значения ряда к базисному
∙ 100 %;
Т бр.февр/ янв = 9,5 / 7,3 ∙ 100 % = 130,14 %;
Т бр.март/янв = 12,8 / 7,3 ∙ 100 % = 175,34 %.
Темп прироста цепной определяется как отношение абсолютного прироста цепного к уровню предшествующего периода
∙ 100 %;
Т цпр.февр/ янв = 2 2 / 7,3 ∙ 100 % = 30,14 %;
Т цпр.март/февр = 3,3 / 9,5 ∙ 100 % = 34,74 %.
Темп прироста базисный определяется как отношение абсолютного базисного прироста к уровню ряда, принятого за базу сравнения для данного ряда
∙ 100 %;
Т бпр.февр/ янв = 2,2 / 7,3 ∙ 100 % = 30,14 %;
Т бпр.март/янв = 5,5 / 7,3 ∙ 100 % = 75,34 %.
Абсолютное значение одного процента прироста (А) рассчитывается как отношение абсолютного прироста цепного к темпу прироста цепному, выраженному в процентах
.
Результаты расчета показателей ряда динамики необходимо представить в табл. 7.2.
Для определения среднего уровня ряда динамики определяется вид ряда. В данном случае ряд интервальный с равными периодами времени и средний уровень рассчитывается по формуле
,
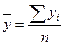где n – число периодов.
млн руб.
Таблица 7.2
Расчет показателей динамики
| Месяц | Выпуск продукции в млн руб. | Абсолютный прирост, млн руб. | Темп роста, % | Темп прироста, % | А | |||
| базис | цепной | базис | цепной | базис | цепной | |||
| я | 7,3 | – | – | – | – | |||
| ф | 9,5 | +2,2 | +2,2 | 130,14 | +30 | +30,14 | 0,073 | |
| м | 12,8 | +5,5 | +3,3 | 134,75 | +75 | +34,75 | 0,095 | |
| а | 12,0 | +4,7 | –0,8 | 93,75 | +64 | –6,25 | 0,128 | |
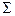
| 41,6 | 12,4 | 4,7 | – | – | – | – | – |
Средний абсолютный прирост цепной рассчитывается по формуле средней арифметической
;
млн руб.
Средний абсолютный прирост базисный рассчитывается по формуле средней арифметической
;
млн руб.
Средние темпы роста и прироста определяется по формулам средней геометрической.
Средний цепной темп роста определяется по формуле средней геометрической величины
;
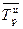
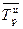
1,18 = 118 %;
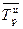
1,18 = 118 %.
Средний ц епной темп прироста
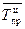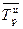= ∙ 100 % – 100 %; 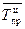= 118 % – 100 % = 18 %;
За рассматриваемый период средний темп роста составил 118 %, то есть выпуск продукции повышался в среднем на 18 %, что в абсолютном выражении составляет 1,57 млн руб.
Средний базисный темп роста определяется по формуле
; 
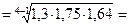1,55 = 155 %.
Средний базисный темп прироста определяется аналогично цепному темпу прироста
155 % – 100 % = 55 %.
По сравнению с январем средний темп роста составил 155 %, то есть среднее повышение выпуска продукции по отношению к январю составило 55 %.
|
|
|
