Распределение, отклонение и среднее распределение доходов среди жильцов подъезда № 2

 

Номер квартиры	2-й подъезд	х-х	\х-х\
		-1050
		-1050
		-850
		-150
		-50
Среднее		Е(х-х)=0

Таким образом, уравнение для среднего отклонения выглядит следующим образом:

(3)

где | ] — символ абсолютной величины (модуля).

Если мы берем каждую отметку и вычитаем из нее среднее мы вычисля­ем ту величину, на которую каждая из отметок (вторая колонка) отличается от среднего (нижняя ячейка второй колонки). Сумма этих отклонений все­гда равна нулю — важное математическое свойство среднего (проверьте это сами, сложив числа в третьей колонке). Поскольку мы интересуемся только

величиной отклонения, а не направле­нием или знаком его, то находим абсо­лютные значения отклонения (четвертая колонка). Затем мы берем их сумму и делим на число отметок, чтобы найти среднее отклонение отметок от среднего; получаем MD = 630 Чем больше среднее отклонение, тем сильнее разброс отметок вокруг среднего

Хотя среднее отклонение и выявляет разброс, чаще для его измерения используются дисперсия и среднеквадратическое отклонение.

Дисперсия (о²) представляет собой сумму квадратов отклонений от сред­него, разделенную на число отметок:

Среднеквадратическое отклонение представляет собою корень квадратный издисперсии:

Чем больше разброс данных вокруг среднего, тем выше значения с² и S. Это означает, что если все данные одинаковы, то а² и Нравны нулю.

Пример расчета дисперсии и среднеквадратического отклонения. В оп­росе, проведенном в конце декабря 1998 г., нижегородцев просили оценить некоторые личностные качества недавно избранного мэра, используя для это­го так называемый семантический дифференциал¹⁷. Этот метод заключается в следующем: респонденту предлагается выразить свое отношение к интере­сующему исследователя качеству по совокупности биполярных шкал (в на­шем случае девятибалльных). Одно из предложенных для оценки качеств мэра — доступность — было выражено с помощью такой шкалы:

Результаты в исследовании распределились следующим образом:

О технике использования этого метода см., например: Родионова Н.В. Семантический диффе­ренциал (обзор литературы)//Социология 4М: методология, методы, математические модели. 1996. № 7. С. 175-200.

Таблица 14 Распределение оценок качества «доступность»

 

Оценочный балл	Частота
Нет ответа
Всего

Отбросив нули (табл. 14), т.е. варианты «нет ответа» (после чего Остано­вится равным 368), мы подсчитываем, что среднее значение оценки (по фор­муле средневзвешенного) составляет:

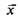= 5,42.

Обратим внимание: если бы мы не отбросили значение «нет ответа», т.е. приняли бы эту позицию за нуль как математическую величину, то получи­ли бы среднее значение:

= 4,67,

т.е. заметно меньшее, нежели рассчитанное нами. Оно более точно в мате­матическом смысле, но искажает социологический смысл, поскольку ведь те, кто не дали ответа, вовсе не выставляли оценку «0», они просто не выстави­ли никакой оценки.

Рассчитаем отклонение от среднего и квадрат отклонения от среднего по каждому баллу (см. табл. 2.11).

Таблица 15 Образец расчета

 

X/ (оценочный балл)
	-4,4	135,52
	-3,4	127,16
	-2,4	230,4
	-1,4	90,16
	-0,4	17,28
	0,6	18,36
	1,6	140,8
	2,6	162,24
	3,6	336,96

Сложив числа крайней правой колонки, мы получим:

= 1258,88; 126

дисперсия: среднеквадратическое отклонение:

Что дает для анализа данных знание дисперсии? Напомним, что «диспер­сия» {dispersion) по-английски означает «разбрасывание, рассеивание»; в дан­ном случае это рассеяние реально полученных эмпирических данных вокруг среднего значения. В зависимости от того, насколько велика (точнее, мала) дисперсия или среднеквадратичное отклонение, мы можем судить, насколь­ко единодушны были в своих оценках респонденты (при меньшем значении дисперсии), или наоборот — насколько сильно они расходятся в своих мне­ниях (при большем значении дисперсии)¹⁸. Сравним, к примеру, разброс оце­нок (по пятибалльной шкале: от 5 — очень важное, до 1 — затрудняюсь отве­тить), которую, в ходе исследования особенностей сексуального поведения, дали респонденты степени влияния на их «сексуальное образование» различ­ных источников информации (табл. 16):

Таблица 16 Оценка степени влияния различных источников на информированность о сфере интимных отношений (в средних знамениях по 5-балльной шкале)

 

Источник	Среднее	S
Сексуальный партнер	3,55	1,36
Супруг(а)	3,12	1,58
Друзья	3,07	1,14
Эротические фильмы	3,02	1,09
Популярные издания	2,93	1,20
Научная литература	2,81	1,15
Эротическая литература	2,81	1,14
Родители	2,36	0,92
Педагоги	2,13	0,82
Другие источники	2,38	1,25

Источник: Данные пилотажного опроса, декабрь 1998 г.

Из этой таблицы помимо сведений о том, что максимальное влияние \м информированность о наиболее интимных сторонах жизни оказывает сек­суальный партнер, а наименьшее — педагоги, мы узнаем также, что с наи­большим единодушием респонденты оценили низкую степень влияния тако­го источника, как педагоги, о чем говорит минимальное значение средне-

¹⁸ Поэтому индексы, основанные на дисперсии, полезно иногда применять при изучении групповси сплоченности.

квадратического отклонения, а наибольшее расхождение в оценках вызвал такой источник, как супруг/супруга, — максимальное значение S (что, воз­можно, связано с большими различиями в индивидуальном опыте).

⇐ Предыдущая25262728293031323334Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: