 |
Задания для самостоятельного решения
|
|
|
|
По имеющимся в следующей таблице данным по группе из 20 студентов заочного отделения необходимо:
1) построить интервальный ряд распределения признака и его график;
2) рассчитать модальное, медианное и среднее значение, установить его типичность с помощью коэффициентов вариации;
| № п/п | Вариант | |||||||||
| Рост, см | Вес, кг | Доход, у.е./мес. | Численн. | Тет-радь, листов | Воз-раст, лет | Соот-ношение «рост/вес» | Стаж работы, мес. | Кол-во друзей, чел. | Время К-ной час. | |
| 3,533 | 8,5 | |||||||||
| 2,623 | 6,2 | |||||||||
| 2,875 | 6,8 | |||||||||
| 3,375 | 12,0 | |||||||||
| 3,000 | 7,5 | |||||||||
| 2,828 | 10,0 | |||||||||
| 3,255 | 7,2 | |||||||||
| 2,726 | 4,2 | |||||||||
| 2,429 | 3,5 | |||||||||
| 2,361 | 9,5 | |||||||||
| 2,342 | 7,8 | |||||||||
| 2,672 | 8,0 | |||||||||
| 2,356 | 6,0 | |||||||||
| 2,559 | 4,8 | |||||||||
| 2,173 | 8,6 | |||||||||
| 2,095 | 10,0 | |||||||||
| 2,342 | 4,5 | |||||||||
| 2,011 | 12,5 | |||||||||
| 2,691 | 10,5 | |||||||||
| 2,021 | 6,5 |
Тема 6. Ряды динамики Практическое занятие № 7:Решение задач на анализ взаимосвязи показателей динамического ряда
Практическое занятие № 8:Решение задач на аналитическое выравнивание показателей динамического ряда.
|
|
|
Цели занятия:
- обобщение и систематизация материала по теме «Ряды динамики»
- сформировать умения: собрать и регистрировать статистическую информацию;
· развитие общих компетенций по ОК 3. Организовывать свою собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
· ОК 4. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.
- ОК 5. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития
· воспитание ответственности за результаты работы.
Форма организации занятия –групповая
Студент должен
- знать:
Основные способы сбора, обработки, анализа и наглядного представления информации - Общие основы статистической науки
- Основные формы и виды действующей статистической отчетности
- Технику расчета статистических показателей, характеризующих социально-экономические явления
- уметь:
Собрать и регистрировать статистическую информацию - Проводить первичную обработку и контроль материалов наблюдения.
- Выполнять расчеты статистических показателей и формулировать основные выводы
Вопросы для проверки готовности студентов к практическому занятию
1.Определение ряда динамики. Практическое использование
2.Виды рядов динамики. Примеры, особенности расчета.
3.Показатели ряда динамики. Характеристика абсолютных показателей ряда.
4. Относительные показатели. Формулы расчета.
5.Средние показатели РД, Методы обработки динамических рядов
Форма отчетности по занятию: письменное решение задач в тетради для практических работ
Задание для практического занятия
и инструктаж по его выполнению
Смертность от болезней системы кровообращения в России за период гг. характеризуется следующим рядом динамики.
|
|
|
| Год | ||||||||||
| Умершие, тыс. чел. | 1163,5 | 1113,7 | 1100,3 | 1094,1 | 1187,8 | 1231,4 | 1253,1 | 1308,1 | 1330,5 | 1287,7 |
Вычислить: абсолютные, относительные, средние изменения и их темпы базисным и цепным способами. Проверить ряд на наличие в нем линейного тренда, на основе которого рассчитать интервальный прогноз на год с вероятностью 95%.
Решение. Любое изменение уровней ряда динамики определяется базисным (сравнение с первым уровнем) и цепным (сравнение с предыдущим уровнем) способами. Оно может быть абсолютным (разность уровней ряда) и относительным (соотношение уровней).
Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда (47), а цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда (48).
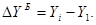(47) 
(48)
По знаку абсолютного изменения делается вывод о характере развития явления: при 
> 0 — рост, при < 0 — спад, при = 0 — стабильность.
В нашей задаче эти изменения определены в 3-м и 4-м столбцах таблицы 5. Для проверки правильности расчетов применяется правило, согласно которому сумма цепных абсолютных изменений равняется последнему базисному. В нашей задаче это правило выполняется: 
= 124,2 и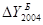 
= 124,2.
Базисное относительное изменение представляет собой соотношение конкретного и первого уровней ряда (49), а цепное относительное изменение представляет собой соотношение конкретного и предыдущего уровней ряда (50).
(49) 
(50)
Относительные изменения уровней — это по существу индексы динамики, критериальным значением которых служит 1. Если они больше ее, имеет место рост явления, меньше ее — спад, а при равенстве единице наблюдается стабильность явления.
В нашей задаче эти изменения определены в 5-м и 6-м столбцах таблицы 5.
Вычитая единицу из относительных изменений, получают темп изменения уровней, критериальным значением которого служит 0. При положительном темпе изменения имеет место рост явления, при отрицательном — спад, а при нулевом темпе изменения наблюдается стабильность явления. В нашей задаче темпы изменения определены в 7-м и 9-м столбцах таблицы 5, а в 8-м и 10-м сделан вывод о характере развития изучаемого явления. Для проверки правильности расчетов применяется правило, согласно которому произведение цепных относительных изменений равняется последнему базисному. В нашей задаче это правило выполняется: 
=1,107 и 
=1,107.
|
|
|
Таблица 5. Вспомогательные расчеты для решения задачи
|
|
|
