 |
Тема 7. Выборочный метод Практическое занятие № 9: Решение задач на расчет показателей выборочного исследования.
|
|
|
|
Практическое занятие № 10: Решение задач на расчет показателей выборочного исследования
Цели занятия:
- обобщение и систематизация материала по теме «Выборочный метод»
- сформировать умения: собрать и регистрировать статистическую информацию;
· развитие общих компетенций по ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.
· ОК 7. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
· ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
· воспитание ответственности за результаты работы.
Форма организации занятия –групповая
Студент должен
- знать:
Основные способы сбора, обработки, анализа и наглядного представления информации - Основные формы и виды действующей статистической отчетности
- Технику расчета статистических показателей, характеризующих социально-экономические явления
- уметь:
Собрать и регистрировать статистическую информацию - Проводить первичную обработку и контроль материалов наблюдения.
- Выполнять расчеты статистических показателей и формулировать основные выводы
Вопросы для проверки готовности студентов к практическому занятию
1.Понятия выборки и практическое применение
2.Виды выборки. Примеры практического использования.
3.Показатели выборки. Формулы расчета.
4.Значение выборочного метода.
5.Ошибки выборки.
Форма отчетности по занятию: письменное решение задач в тетради для практических работ
|
|
|
Задание для практического занятия
и инструктаж по его выполнению
На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за месяц:
| Доход, у.е. | до 300 | 300-500 | 500-700 | 700-1000 | более 1000 |
| Число рабочих |
С вероятностью 0,950 определить:
1) среднемесячный размер дохода работников данного предприятия;
2) долю рабочих предприятия, имеющих месячный доход более 700 у.е.;
3) необходимую численность выборки при определении среднемесячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е.;
4) необходимую численность выборки при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.
Решение. Выборочный метод (выборка) используется, когда применение сплошного наблюдения физически невозможно из-за огромного массива данных или экономической нецелесообразности. Учитывая, что на основе выборочного обследования нельзя точно оценить изучаемый параметр (например, среднее значение –  или долю какого-то признака – р) генеральной совокупности, необходимо найти пределы, в которых он находится. Для этого необходимо определить изучаемый параметр по данным выборки (выборочную среднюю –
или долю какого-то признака – р) генеральной совокупности, необходимо найти пределы, в которых он находится. Для этого необходимо определить изучаемый параметр по данным выборки (выборочную среднюю – 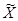 и/или выборочную долю – w) и его дисперсию (Дв). Для этого построим вспомогательную таблицу 3.
и/или выборочную долю – w) и его дисперсию (Дв). Для этого построим вспомогательную таблицу 3.
Таблица 3. Вспомогательные расчеты для решения задачи
| Xi | fi | Х И | X И fi | (Х И - 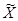 )2 )2
| (Х И - 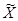 )2fi )2fi
|
| до 300 | |||||
| 300 - 500 | |||||
| 500 - 700 | |||||
| 700 - 1000 | |||||
| более 1000 | |||||
| Итого |
По формуле (18) получим средний доход в выборке: 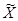 = 57100/100 = 571 (у.е.). Применив формулу (33) и рассчитав ее числитель в последнем столбце таблицы, получим дисперсию среднего выборочного дохода: Дв = 4285900/100 = 42859.
= 57100/100 = 571 (у.е.). Применив формулу (33) и рассчитав ее числитель в последнем столбце таблицы, получим дисперсию среднего выборочного дохода: Дв = 4285900/100 = 42859.
Затем необходимо определить предельную ошибку выборки по формуле (39)[1]:
|
|
|
 =t
=t  , (1)
, (1)
где t – коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки;  – средняя ошибка выборки, определяемая для повторной выборки по формуле 2, а для бесповторной – по формуле3:
– средняя ошибка выборки, определяемая для повторной выборки по формуле 2, а для бесповторной – по формуле3:
 =
=  , (2
, (2  =
= 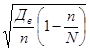 , (3)
, (3)
где n – численность выборки; N – численность генеральной совокупности.
В нашей задаче выборка бесповторная, значит, применяя формулу (41), получим среднюю ошибку выборки при определении среднего возраста в генеральной совокупности:  =
=  = 19,640 (у.е.).
= 19,640 (у.е.).
Для определения средней ошибки выборки при определении доли рабочих с доходами более 700 у.е. в генеральной совокупности необходимо определить дисперсию этой доли. Дисперсия доли альтернативного признака w (признак, который может принимать только два взаимоисключающих значения – например, больше или меньше определенного значения) определяется по формуле (2):
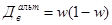 .(42)
.(42)
В нашей задаче долю альтернативного признака (рабочие с доходами более 700 у.е.) найдем как отношение числа таких рабочих к общему числу рабочих в выборке: w = 20/100 = 0,2 или 20%. Теперь определим дисперсию этой доли по формуле (42):  =0,2*(1-0,2) = 0,16. Теперь можно рассчитать среднюю ошибку выборки по формуле (41):
=0,2*(1-0,2) = 0,16. Теперь можно рассчитать среднюю ошибку выборки по формуле (41):  =
=  = 0,038 или 3,8%.
= 0,038 или 3,8%.
Значения вероятности  и коэффициента доверия t имеются в математических таблицах нормального закона распределения вероятностей (если в выборке более 30 единиц), из которых в статистике широко применяются сочетания, приведенные в таблице 4:
и коэффициента доверия t имеются в математических таблицах нормального закона распределения вероятностей (если в выборке более 30 единиц), из которых в статистике широко применяются сочетания, приведенные в таблице 4:
Таблица 4. Значения интеграла вероятностей Лапласа

| 0,683 | 0,866 | 0,950 | 0,954 | 0,988 | 0,997 |
| t | 1,5 | 1,96 | 2,5 |
В нашей задаче  = 0,950, значит t = 1,96 (то есть предельная ошибка выборки в 1,96 раза больше средней). Предельная ошибка выборки по формуле (39) будет равна:
= 0,950, значит t = 1,96 (то есть предельная ошибка выборки в 1,96 раза больше средней). Предельная ошибка выборки по формуле (39) будет равна:  = 1,96*19,64 = 38,494 (у.е.) при определении среднего дохода;
= 1,96*19,64 = 38,494 (у.е.) при определении среднего дохода;  = 1,96*0,038 = 0,075 или 7,5% при определении доли рабочих с доходами более 700 у.е.
= 1,96*0,038 = 0,075 или 7,5% при определении доли рабочих с доходами более 700 у.е.
После расчета предельной ошибки находят доверительный интервал обобщающей характеристики генеральной совокупности по формуле (43) – для средней величины и по формуле (44) – для доли альтернативного признака:
(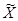 -
-  )
) 

 (
(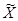 +
+  )(43) (w -
)(43) (w -  )
)  p
p  (w +
(w +  )(44)
)(44)
В нашей задаче по формуле (43): 571-38,494 

 571+38,494 или 532,506 у.е.
571+38,494 или 532,506 у.е. 

 609,494 у.е., то есть средний доход всех рабочих предприятия с вероятностью 95% будет лежать в пределах от 532,5 до 609,5 у.е.
609,494 у.е., то есть средний доход всех рабочих предприятия с вероятностью 95% будет лежать в пределах от 532,5 до 609,5 у.е.
|
|
|
Аналогично определяем доверительный интервал для доли по формуле (44): 0,2-0,075  p
p  0,2+0,075 или 0,125
0,2+0,075 или 0,125  p
p  0,275, то есть доля рабочих с доходами более 700 у.е. на всем предприятии с вероятностью 95% будет лежать в пределах от 12,5% до 27,5%.
0,275, то есть доля рабочих с доходами более 700 у.е. на всем предприятии с вероятностью 95% будет лежать в пределах от 12,5% до 27,5%.
При разработке программы выборочного наблюдения очень часто задается конкретное значение предельной ошибки ( ) и уровень вероятности (
) и уровень вероятности ( ). Неизвестной остается минимальная численность выборки (n), обеспечивающая заданную точность. Ее можно получить, если подставить формулу (40) или (41) в формулу (39) и выразить из них n. В результате получатся формулы для вычисления необходимой численности повторной (45) и бесповторной (46) выборок.
). Неизвестной остается минимальная численность выборки (n), обеспечивающая заданную точность. Ее можно получить, если подставить формулу (40) или (41) в формулу (39) и выразить из них n. В результате получатся формулы для вычисления необходимой численности повторной (45) и бесповторной (46) выборок.
|
|
|


