 |
Допустимые степени деформации при волочении труб
|
|
|
|
При волочении сечение трубы за один проход может быть уменьшено только до определенных размеров, при получении которого обеспечивается стабильность (устойчивость) процесса при заданном качестве готовых труб. В работах И. Л. Перлина, В. Л. Колмогорова, B. И. Уральского, Ю. Ф. Шевакина и др. выбор разовой допустимой степени деформации 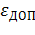 определяется через напряжение волочения
определяется через напряжение волочения  в конце выходного участка трубы, которое не должно превышать сопротивление деформации металла трубы, т.е. выходящий из волоки металл должен иметь некоторый запас прочности, определяемый коэффициентом запаса:
в конце выходного участка трубы, которое не должно превышать сопротивление деформации металла трубы, т.е. выходящий из волоки металл должен иметь некоторый запас прочности, определяемый коэффициентом запаса:
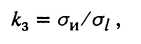
где 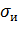 — истинный предел текучести протянутой трубы.
— истинный предел текучести протянутой трубы.
Процесс волочения труб протекает стабильно (по данным С. И. Борисова), если коэффициент запаса прочности составляет:
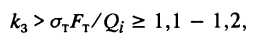
где 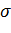 Т - предел текучести металла наклепанной трубы.
Т - предел текучести металла наклепанной трубы.
Максимальная деформация 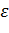 доп, допустимая по прочности сечения выходящей трубы, зависит от соотношения толщины стенки к диаметру трубы.
доп, допустимая по прочности сечения выходящей трубы, зависит от соотношения толщины стенки к диаметру трубы.
При волочении тонкостенных и особотонкостенных труб степень деформации трубы при безоправочном волочении ограничивается устойчивостью трубы, а не прочностью выходного сечения трубы. Ввиду отсутствия оправки с увеличением обжатия труба в очаге деформации может потерять поперечную устойчивость (образование продольных складок) Зависимость критической деформации от отношения S/DT, по данным С. И. Борисова, может быть выражена уравнением:
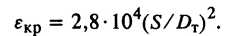 (8)
(8)
Ниболее вероятное место возможной потери устойчивости начало контактной поверхности, где толщина стенки минимальна, а радиальное давление максимально. Критическая величина нормального давления, вызывающая потерю устойчивости трубы, может быть определена по данным И. Л. Перлина и М. 3. Ерманка:
|
|
|
 (9)
(9)
где Е - модуль упругости; S - толщина стенки трубы;  - коэффициент Пуансона; R - средний радиус сечения трубы.
- коэффициент Пуансона; R - средний радиус сечения трубы.
Минимальное отношение S/DT, при котором сохраняется устойчивость трубы:
 (10)
(10)
В связи со сложностью расчетов по приведенной формуле из-за отсутствия зависимостей, определяющих 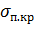 работе И. Л. Перлина и М. 3. Ерманка рекомендуется во избежание потери устойчивости трубы применять уменьшение диаметра трубы, не превышающее за один проход шестикратной толщины стенки, т. е. D3- DT< 6S.
работе И. Л. Перлина и М. 3. Ерманка рекомендуется во избежание потери устойчивости трубы применять уменьшение диаметра трубы, не превышающее за один проход шестикратной толщины стенки, т. е. D3- DT< 6S.
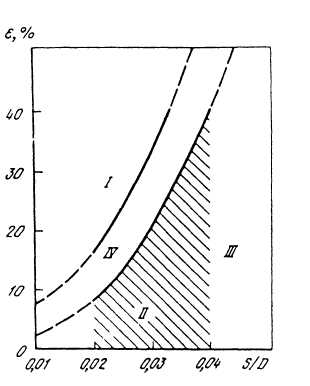
|
Рис. 65. Зависимость критической степени деформации от отношения S/DT: I - область полной потери устойчивости; II -область допустимых деформаций; III - область, где величина деформации лимитируется прочностью выходящей трубы; IV -область колеблющейся устойчивости трубы
При волочении труб на неподвижной (короткой) оправке степень деформации определяется пластическими свойствами материала трубы. Для каждого материала устанавливается допустимая деформация  доп до отжига, при которой полностью или в значительной степени исчерпываются пластические свойства. Допустимые (рассчитанные) величины вытяжки должны быть меньше предельных на 8-15% с учетом различных производственных факторов, снижающих деформируемость (разностенность заготовки, неравномерность механических свойств по длине, качество смазки, качество инструмента и др.).
доп до отжига, при которой полностью или в значительной степени исчерпываются пластические свойства. Допустимые (рассчитанные) величины вытяжки должны быть меньше предельных на 8-15% с учетом различных производственных факторов, снижающих деформируемость (разностенность заготовки, неравномерность механических свойств по длине, качество смазки, качество инструмента и др.).
Число необходимых отжигов:

где  - суммарная вытяжка от заготовки к готовой трубе.
- суммарная вытяжка от заготовки к готовой трубе.
Вытяжки по проходам назначают исходя из допустимого напряжения волочения с учетом соблюдения условий, обеспечивающих необходимый запас прочности.
Величина допустимых вытяжек для различных материалов может быть определена по формуле, рекомендуемой Н. П. Белоусовым:
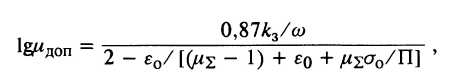 (11)
(11)
где 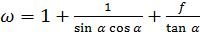 , k3 - коэффициент запаса прочности;
, k3 - коэффициент запаса прочности; 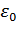 - относительная деформация за данный проход;
- относительная деформация за данный проход; 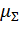 - вытяжка за проход;
- вытяжка за проход; 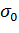 - экстраполированный предел текучести; П -модуль пластичности материала.
- экстраполированный предел текучести; П -модуль пластичности материала.
|
|
|
Для определения степени деформации при волочении на самоустанавливающейся (плавающей) оправке необходимо установить соотношение между уменьшением диаметра трубы и уменьшением толщины стенки, которое определяет устойчивость процесса.
Исследования устойчивости процесса волочения на плавающей оправке, выполненные К. В. Гаген-Торном, показали, что при малых вытяжках (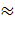 1,3) может произойти только небольшое уменьшение толщины стенки и для достаточно эффективного уменьшения толщины стенки необходимо применять большие вытяжки (
1,3) может произойти только небольшое уменьшение толщины стенки и для достаточно эффективного уменьшения толщины стенки необходимо применять большие вытяжки (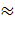 1,5). При волочении на плавающей оправке вытяжка за проход:
1,5). При волочении на плавающей оправке вытяжка за проход:
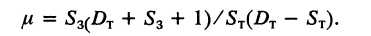 (12)
(12)
Приведенную формулу применяют для определения размеров заготовки по допустимой вытяжке за проход, предварительно рассчитанной из условия прочности протягиваемой трубы.
В табл. 33 приведены допустимые коэффициенты вытяжки при различных способах волочения труб из углеродистой стали.
Таблица 33. Допустимые коэффициенты вытяжки при волочении труб
| Способ волочения | Коэффициент вытяжки | 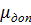
| для сталей | |||
| Без оправки | 1,5 | 1,5 | 1,4 | 1,35 | ||
| На короткой оправке | 1,7 | 1,7 | 1,55 | 1,45 | ||
| На плавающей оправке | 1,75 | 1,75 | 1,6 | 1,5 | ||
Расчет усилий при волочении труб
Аналитические методы определения усилий волочения труб основаны на законах механики пластически деформируемого тела и условиях пластичности и определяются совместным решением дифференциального уравнения равновесия сил, действующих на выделенный в очаге элементарный объем металла, и уравнений пластичности для каждого элемента очага деформации.
Усилие волочения QB, под действием которого труба протягивается через волоку, принято определять по напряжению волочения
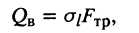 (13)
(13)
где 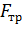 - площадь поперечного сечения трубы после волочения.
- площадь поперечного сечения трубы после волочения.
Ниже приведены формулы расчета напряжений при безопра-вочном волочении труб.
1.1. Формула И. Л. Перлина
 (14)
(14)
где 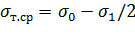 - среднее значение предела текучести материала до и после деформации,
- среднее значение предела текучести материала до и после деформации,
или

Зависимость 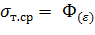 может быть получена методом регрессионного анализа на основании экспериментальных данных. Значение
может быть получена методом регрессионного анализа на основании экспериментальных данных. Значение 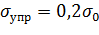 - напряжение на границе упругой и пластической зон; ао- предел прочности исходного материала (заготовки);
- напряжение на границе упругой и пластической зон; ао- предел прочности исходного материала (заготовки);
|
|
|
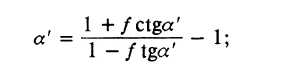
f- коэффициент трения; а' - приведенный угол волоки:
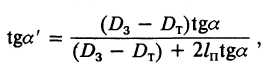
D3, DT - диаметры заготовки и трубы; D3Cp, DTCp - средние диаметры заготовки и трубы (D3cp = d3 + S 3; DTCp = dT + ST); 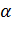 -половина угла входного конуса волоки;
-половина угла входного конуса волоки;  - длина калибрующего пояска волоки.
- длина калибрующего пояска волоки.
1.2. Формула Л. Е. Алыпевского
 (15)
(15)
1.3. Формула Е. Зибеля
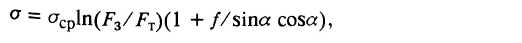 (16)
(16)
где 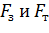 - площади поперечного сечения заготовки и трубы.
- площади поперечного сечения заготовки и трубы.
В табл. 34 приведены результаты расчета напряжения безоправочного волочения по формулам различных авторов.
Таблица 34. Расчетные и экспериментальные напряжения при безоправочном волочении
Размер трубы 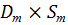 , мм , мм
| Напряжение, кН | ||||
| до волочения | после волочения | расчетное по формулам | экспериментальное | ||
| (14) (13.14) | (15) | (16) | |||
| 47,0 х 6,0 42,0 х 2,6 40,0 х 1,9 38,0 х 1,7 34,0 х 2,7 32,0 х 3,9 | 42,0 х 6,0 34,0 х 2,6 35,0 х 1,9 30,0 х 1,7 27,0 х 2,7 26,0 х 3,9 | 147 77 42 48 68 89 | 147,7 76,3 54,8 57,0 72,9 | 79,5 50,4 67,5 87,9 |
1.4.Формула М. М. Бернштейна
 (17)
(17)
Формула М. М. Бернштейна наиболее проста, но она эмпирическая, поэтому при учете влияния различных факторов процесса на напряжение волочения следует пользоваться формулами И. Л. Перлина и Л. Е. Алыыевского.
Напряжение при волочении на неподвижной (короткой) оправке можно определить по следующим формулам.
2.1. Формула И. Л. Перлина
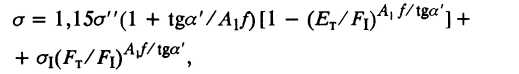 (18)
(18)
где 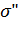 - среднее значение предела текучести материала в зоне обжатия стенки:
- среднее значение предела текучести материала в зоне обжатия стенки: 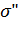 =
= 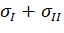 ; здесь
; здесь 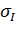 - предел текучести материала в конце зоны осаживания;
- предел текучести материала в конце зоны осаживания; 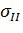 - предел текучести материала в конце зоны обжатия стенки;
- предел текучести материала в конце зоны обжатия стенки;
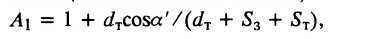
где dT - внутренний диаметр трубы;  - площадь поперечного сечения трубы в конце зоны осаживания;
- площадь поперечного сечения трубы в конце зоны осаживания; 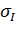 - растягивающее осевое напряжение на границе зон обжатия и осаживания стенки, определяемое по формуле И. Л. Перлина для безоправочного волочения.
- растягивающее осевое напряжение на границе зон обжатия и осаживания стенки, определяемое по формуле И. Л. Перлина для безоправочного волочения.
2.2. Формула Л. Е. Альшевского
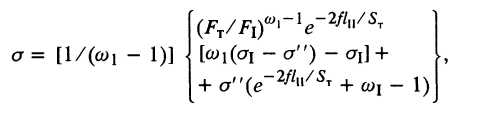 (19)
(19)
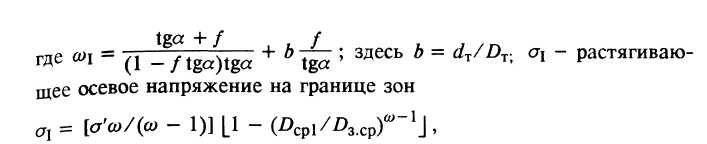
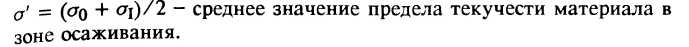
2.3. Формула В. А. Кочкина
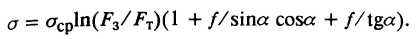 (20)
(20)
При волочении на короткой неподвижной оправке на стержень действует растягивающее усилие, величину которого можно определить по формуле И. Л. Перлина:
|
|
|
 (21)
(21)

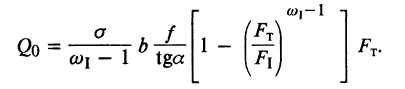 (22)
(22)
Напряжение при волочении на подвижной длинной оправке определяют по следующим формулам.
3.1. Формула И. Л. Перлина
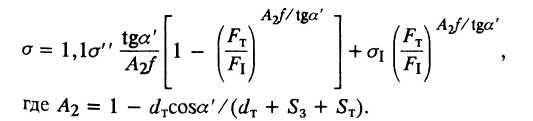 (23)
(23)
3.2. Формула Л. Е. Альшевского
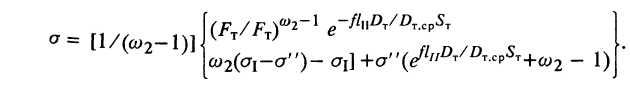 (24)
(24)
Усилие на оправке при ее волочении с трубой (по Л. Е. Альшевскому):
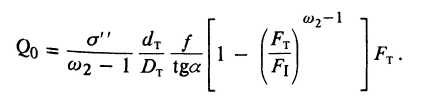 (25)
(25)
С учетом усилия на оправке общее усилие волочения:
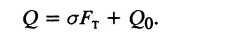 (26)
(26)
3.3. Формула М. М. Бернштейна
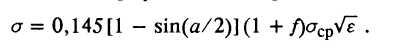 (27)
(27)
При расчетах напряжений волочения можно принимать коэффициент трения равным 0,11 - 0,13 для углеродистой и низколегированной сталей.
Для определения тягового усилия волочения при практических расчетах можно пользоваться упрощенными формулами П. Т. Емельяненко и Л. Е. Алыпевского:
при волочении без оправки
 (28)
(28)
при волочении на неподвижной оправке
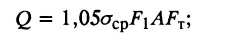 (29)
(29)
при волочении на подвижной оправке
 (30)
(30)
Здесь 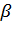 = 1,0— 1,15- коэффициент, учитывающий влияние среднего главного напряжения (для толстостенных труб
= 1,0— 1,15- коэффициент, учитывающий влияние среднего главного напряжения (для толстостенных труб 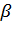 = 1,0);
= 1,0); 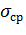 -среднее значение предела текучести материала трубы;
-среднее значение предела текучести материала трубы;
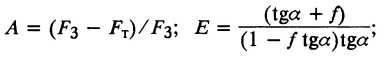
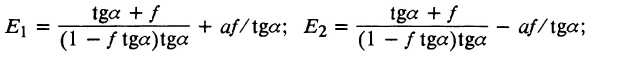
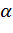 — угол наклона стенки волоки к оси волочения;
— угол наклона стенки волоки к оси волочения; 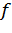 - коэффициент трения между оправкой, волокой и трубой; а - отношение радиуса оправки к среднему конечному радиусу трубы.
- коэффициент трения между оправкой, волокой и трубой; а - отношение радиуса оправки к среднему конечному радиусу трубы.
Оптимальный угол увеличивается с повышением обжатия и коэффициента вытяжки. На основании опытных данных установлено, что оптимальный угол наклона конусной части канала волоки равен 0,210 - 0,245 рад, коэффициент трения при этом равен 0,1 - 0,15.
|
|
|


