 |
Коммутативность операторов и одновременная измеримость физических величин.
|
|
|
|
Введем понятие коммутатора
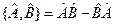
Если мы имеем  , то предполагается, что на некоторую функцию
, то предполагается, что на некоторую функцию  сначала действует
сначала действует  , а потом на все действует
, а потом на все действует  . Если
. Если  , то операторы
, то операторы  и
и  коммутативны. Причем физические величины, соответствующие этим операторам одновременно измеримы. Или говорят, что эти операторы имеют общий базис. То есть, все собственные функции этих операторов можно выбрать общими. Разложим
коммутативны. Причем физические величины, соответствующие этим операторам одновременно измеримы. Или говорят, что эти операторы имеют общий базис. То есть, все собственные функции этих операторов можно выбрать общими. Разложим  по базису.
по базису.
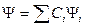
Подействуем на  коммутатором:
коммутатором:
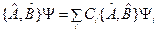
Используем то, что  образуют общий базис
образуют общий базис 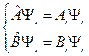 :
:
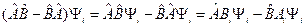
Числа с оператором коммутируют (т. к. операторы эрмитовы), тогда:

В результате получаем:

То есть, если физические величины одновременно измеримы, то коммутатор соответствующих им операторов равен нулю. Также справедливо обратное утверждение - если коммутатор операторов обращается в нуль, то физические величины соответствующие этим операторам одновременно измеримы. Докажем это утверждение:
Пусть  собственная функция оператора
собственная функция оператора 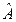 , т.е.
, т.е. 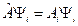 . Подставляем ее в коммутатор:
. Подставляем ее в коммутатор:
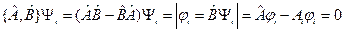
Тогда получим 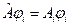 . Мы рассматриваем невырожденный спектр. Это значит, что одному собственному значению соответствует единственная собственная функция. Разница между функциями
. Мы рассматриваем невырожденный спектр. Это значит, что одному собственному значению соответствует единственная собственная функция. Разница между функциями  и
и 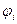 только до константы. Пусть эта константа -
только до константы. Пусть эта константа - 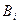 , тогда
, тогда  . Но
. Но 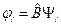 , тогда
, тогда 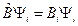 . Мы получили, что функция
. Мы получили, что функция  удовлетворяет задаче на собственные функции и собственные значения для оператора
удовлетворяет задаче на собственные функции и собственные значения для оператора  . Это можно показать для любой собственной функции оператора
. Это можно показать для любой собственной функции оператора  . Тогда из коммутативности операторов
. Тогда из коммутативности операторов  и
и  следует общность базисов.
следует общность базисов.
Величины  и
и 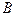 , которым соответствуют коммутирующие операторы, могут быть одновременно измеримы и, следовательно, могут образовывать полный набор динамических переменных. Полный набор динамических переменных полностью задает состояние системы. Но операторы
, которым соответствуют коммутирующие операторы, могут быть одновременно измеримы и, следовательно, могут образовывать полный набор динамических переменных. Полный набор динамических переменных полностью задает состояние системы. Но операторы  и
и  должны быть независимы.
должны быть независимы.
|
|
|
§15. Операторы координаты  , импульса
, импульса  , момента импульса
, момента импульса  , энергии
, энергии  .
.
Будем использовать координатное представление ( -представление). Будем рассматривать систему из одной материальной точки. Действие
-представление). Будем рассматривать систему из одной материальной точки. Действие  сводитсяк умножению на вектор
сводитсяк умножению на вектор 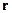 , т. е.
, т. е. 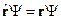 (это определение действия оператора
(это определение действия оператора  ).
).

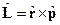
Здесь строго соблюдается последовательность операторов при раскрытии векторного произведения, например, первая компонента:
 ,
,
однако для частного случая декартовых координат порядок операторов не существенен.
Оператор энергии или гамильтониан 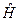 :
:
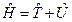 ,
,
здесь  - оператор кинетической энергии,
- оператор кинетической энергии, 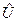 - оператор потенциальной энергии. Для одной материальной точки гамильтониан имеет вид:
- оператор потенциальной энергии. Для одной материальной точки гамильтониан имеет вид:
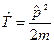

Переменная t – признак внешнего нестационарного поля.

Тут присутствует  и
и  , но
, но 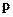 и
и 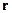 одновременно неизмеримы, тогда потенциальная и кинетическая энергия в квантовой механике не могут быть одновременно измеримыми. В квантовой механике существует понятие “энергия частицы”, но порознь вводить энергию нельзя, иначе либо
одновременно неизмеримы, тогда потенциальная и кинетическая энергия в квантовой механике не могут быть одновременно измеримыми. В квантовой механике существует понятие “энергия частицы”, но порознь вводить энергию нельзя, иначе либо 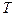 , либо
, либо  оказываются неизвестными.
оказываются неизвестными.
§16. Решение задачи на собственные функции и собственные значения для оператора  .
.
Оператор импульса – оператор с непрерывным спектром собственных значений.
 (16.1)
(16.1)
Мы рассматриваем координатное представление, тогда 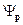 - функция координат.
- функция координат.
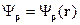
Оператор  векторный, он имеет три компоненты:
векторный, он имеет три компоненты:

Например:
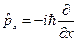 (16.2)
(16.2)
Тогда уравнение (16.1) разбивается на три независимых члена, т.к. операторы 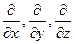 коммутируют. Существует утверждение, что если
коммутируют. Существует утверждение, что если 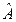 можно представить в виде суммы коммутирующих операторов:
можно представить в виде суммы коммутирующих операторов:
 ,
, 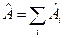 ,
,
то задача на собственные функции и собственные значения 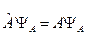 распадается на подзадачи этих коммутаторов:
распадается на подзадачи этих коммутаторов:


Для задачи (16.1) имеем:
 ,
,
где i принимает значения 1,2,3
Решим случай i=1, тогда
 (16.3)
(16.3)
Подставляем (16.2) в (16.3) и временно опустим индекс px у 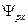 , тогда имеем
, тогда имеем
|
|
|

т.к. 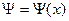 - функция одной переменной, то:
- функция одной переменной, то:
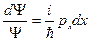

здесь  - число, собственное значение.
- число, собственное значение.

При решении задачи получили, что p имеет непрерывный спектр на всей числовой оси. Т. е.  - не квантуется. Найдем
- не квантуется. Найдем 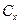 . Используем условие ортонормированности:
. Используем условие ортонормированности:

В нашем случае:
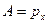 ,
, 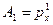
Тогда:
 (16.4)
(16.4)
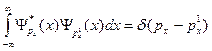 .
.
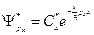 .
.
Обозначим 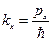 .
.
 .
.
Тогда
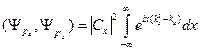
Интеграл дает с точностью до множителя 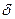 - функцию, поскольку:
- функцию, поскольку:

Используем следующее свойство 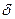 -функции:
-функции:
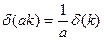 .
.
В нашем случае получим
 ,
,
тогда
 (16.5)
(16.5)
Сравнивая (16.5) и (16.4) получим:
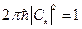
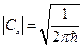
В связи с тем, что волновые функции в квантовой механике определены с точностью до фазового множителя, то
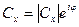 .
.
Фаза 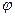 точно не определена, и ее можно отнести к самой волновой функции. Такая неоднозначность принципиальна и не может быть устранена, однако она несущественна, так как не отражается ни на каких физических величинах. Таким образом:
точно не определена, и ее можно отнести к самой волновой функции. Такая неоднозначность принципиальна и не может быть устранена, однако она несущественна, так как не отражается ни на каких физических величинах. Таким образом: 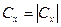 . Мы получили
. Мы получили

Теперь запишем  - для трёх мерного случая:
- для трёх мерного случая:
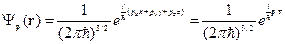 (16.6)
(16.6)
Функция (16.6) удовлетворяет условию нормировки (16.4).
В импульсном представлении: 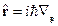

§17. Решение задачи на собственные функции и собственные значения для оператора  .
.
Если в классической механике рассматривать  , то
, то
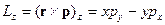 .
.
Если полученному выражению поставить в соответствие оператор в квантовой механике, то он может быть записан в виде:
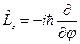 ,
,
где 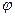 - угол поворота вокруг оси
- угол поворота вокруг оси 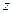 .
.
Рассмотрим задачу на собственные функции и собственные значения для оператора  :
:
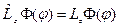
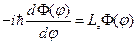 ,
,
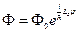
Мы накладываем на функцию  условие периодичности, т. к. угол
условие периодичности, т. к. угол 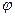 меняется от
меняется от 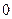 до
до  , т. е.:
, т. е.:
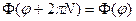
Используя данное ограничение можно записать:
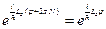


 ,
,
где N и M целые числа, значит 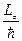 тоже должно быть целым:
тоже должно быть целым:

 ,
,
где 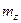 - целое безразмерное число. Из условия периодичности получили квантованность проекции орбитального момента на ось z. Спектр собственных значений оператора
- целое безразмерное число. Из условия периодичности получили квантованность проекции орбитального момента на ось z. Спектр собственных значений оператора  дискретный. Так как
дискретный. Так как 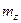 целое число, то функция
целое число, то функция  приобретает индекс:
приобретает индекс:
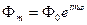
Найдем константу  . Запишем условие нормировки
. Запишем условие нормировки 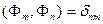 :
:
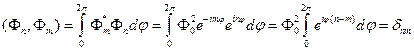
При  интеграл дает
интеграл дает 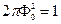 . В результате получаем выражение для
. В результате получаем выражение для 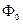 :
:

Тогда имеем для уравнения  собственную волновую функцию
собственную волновую функцию

Таким образом, спектр собственных значений оператора 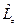 дискретный, а собственные функции нормируемые.
дискретный, а собственные функции нормируемые.
§ 18. Вычисление коммутаторов, содержащих операторы  .
.
Для оператора  :
:

Найдем  , где
, где  - есть функция
- есть функция  и
и  , т.е.
, т.е. 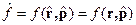 - координатное представление.
- координатное представление.
|
|
|
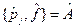
Подействуем этим коммутатором на некоторую произвольную функцию  :
:
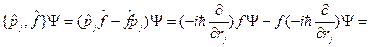
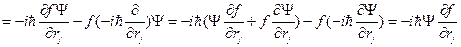
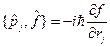 (18.1)
(18.1)
Аналогичный результат для оператора  в импульсном представлении:
в импульсном представлении:

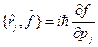 , (18.2)
, (18.2)
здесь 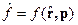 .
.
Рассмотрим частные случаи формул (18.1) и (18.2):
1. 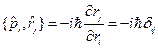 , здесь
, здесь 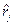 играет роль функции
играет роль функции 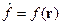 .
.
2. 
3.  , здесь
, здесь  потенциальная энергия - функция координат и времени.
потенциальная энергия - функция координат и времени.
3a. 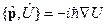
4. 
5.  , здесь импульсное представление, таким образом
, здесь импульсное представление, таким образом 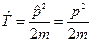 .
.
5a.  .Для одной материальной точки
.Для одной материальной точки 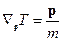 , тогда:
, тогда:
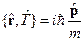
6.  - координатное представление.
- координатное представление.
7. 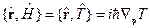 - импульсное представление.
- импульсное представление.
Рассмотрим соотношение для оператора 

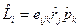
Используем дополнительное соотношение:

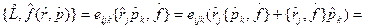 {используем (18.1) и (18.2):
{используем (18.1) и (18.2): 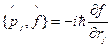 ,
,  }
} 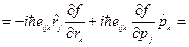 {
{ 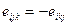 , тогда второе слагаемое
, тогда второе слагаемое 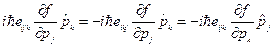 } =
} = 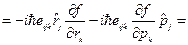 {в классической математике измерение компонента вектора при бесконечно малом повороте:
{в классической математике измерение компонента вектора при бесконечно малом повороте:
 ,
, 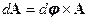
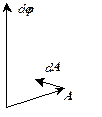
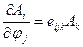 это отношение справедливо и в квантовой теории поля:
это отношение справедливо и в квантовой теории поля:
 }={
}={ 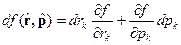 }={
}={  ,
,
 . В общем случае импульс и координата не коммутируют, тогда функция координат и импульсов и импульс, координата и функция координат и импульсов не коммутируют. Если f – функция скалярная, тогда она не меняется при вращении. В этом случае, чтобы
. В общем случае импульс и координата не коммутируют, тогда функция координат и импульсов и импульс, координата и функция координат и импульсов не коммутируют. Если f – функция скалярная, тогда она не меняется при вращении. В этом случае, чтобы 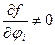 , то f – векторная функция.}
, то f – векторная функция.} 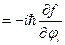 (где f есть компонента некоторой векторной величины, т. е.
(где f есть компонента некоторой векторной величины, т. е.  .
.
Тогда перепишем  в виде
в виде  :
:
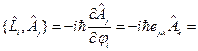 {меняем местами индексы}
{меняем местами индексы} 
Тогда для любой векторной функции имеем:

Здесь вместо  можно подставить, например,
можно подставить, например, 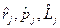
 - коммутатор
- коммутатор  с любым скаляром равен нулю.
с любым скаляром равен нулю.
Получим:
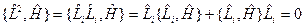
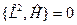
Волновое уравнение
Надо сформулировать уравнение функции, которая описывала бы квантово-механическую систему.
Это уравнение было получено Шредингером интуитивным путем. Оно ниоткуда не выводится.
Приведем некоторые соотношения в пользу уравнения Шредингера:
Норма волновой функции: 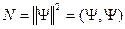
 - вероятность обнаружить динамические переменные в интервале
- вероятность обнаружить динамические переменные в интервале 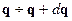 .
.
Наложим на 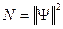 - условие ее сохранения во времени.
- условие ее сохранения во времени.  - это физическое требование, поскольку
- это физическое требование, поскольку 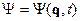 , то
, то 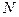 также функция времени.
также функция времени.
На базе ограничения  получим некоторые ограничения на
получим некоторые ограничения на 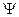 .
.
Обозначим 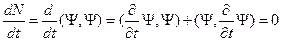 . Мы знаем, что
. Мы знаем, что 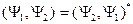 , таким образом
, таким образом 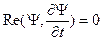 . Тогда само скалярное произведение
. Тогда само скалярное произведение  - чисто мнимое число.
- чисто мнимое число.
Но  - число вещественное. Отсюда можно представить
- число вещественное. Отсюда можно представить
|
|
|
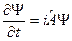 (19.1)
(19.1)
Здесь мнимая единица из соотношения 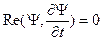 . Т. к. в (*) стоит линейный оператор
. Т. к. в (*) стоит линейный оператор  , то это соотношение удовлетворяет принципу суперпозиции.
, то это соотношение удовлетворяет принципу суперпозиции.
Подставим (19.1) в равенство 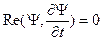 , тогда
, тогда

 - эта величина должна быть чисто вещественной, тогда оператор
- эта величина должна быть чисто вещественной, тогда оператор  - эрмитов:
- эрмитов: 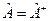 .
.
Свойства оператора  :
:
В пределе перехода к классической механике:  , то
, то 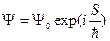 , где S – действие из классической механики. Причем
, где S – действие из классической механики. Причем  , тогда рассматривая
, тогда рассматривая
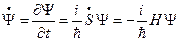 , (19.2)
, (19.2)
где  - функция Гамильтона.
- функция Гамильтона.
В нашем случае  , тогда учитывая предельный переход
, тогда учитывая предельный переход  и (19.2), то:
и (19.2), то: 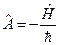 .
.
Получили волновое уравнение:

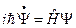 - нестационарное уравнение Шредингера (волновое уравнение).
- нестационарное уравнение Шредингера (волновое уравнение).
Каждой системе ставится в соответствие Гамильтониан, решаем с гамильтонианом уравнение Шредингера и получаем волновую функцию которая определяет эволюцию системы.
|
|
|


