 |
Симметричное и антисимметричное состояния.
|
|
|
|
Чтобы построить конкретные функции будем рассматривать ансамбль независимых частиц, т. е. они между собой не взаимодействуют, но могут находиться во внешнем поле.
Для i -ой частицы во внешнем поле:

Так как частицы одинаковые, то их массы одинаковые, т. е.  .
.
Полный оператор
 (51.1)
(51.1)
Для  одинаковые аналитические выражения (закон один), но здесь разные координаты.
одинаковые аналитические выражения (закон один), но здесь разные координаты.
Когда оператор 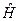 представим в виде (51.1), то можно провести разделение переменных
представим в виде (51.1), то можно провести разделение переменных
 .
.
Тогда уравнение

разбивается на N одинаковых уравнений:

 - волновая одночастичная функция.
- волновая одночастичная функция.
 - это набор квантовых чисел, характеризующих одночастичное состояние.
- это набор квантовых чисел, характеризующих одночастичное состояние.
Тогда
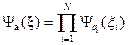 (51.2)
(51.2)
 - это все квантовые числа, относящиеся к рассматриваемому ансамблю.
- это все квантовые числа, относящиеся к рассматриваемому ансамблю.
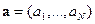
Причем
 ,
,
где
 .
.
Учтем действие оператора перестановки:
1) Рассмотрим симметричные состояния.

Однако из (51.2) при перестановке мы получаем другую функцию. Но в (51.2) функция еще не симметричная. Симметризуем ее:

Здесь сумма по всем нетождественным перестановкам частиц.
 - постоянная нормировки
- постоянная нормировки
 ,
,
где
 .
.
Рассмотрим случай двух частиц

Для данного случая
 .
.
Так как бозоны могут находиться в неограниченном количестве в одном и том же состоянии, то здесь когда говорим о нетождественных состояниях, то имеем в виду, что эта перестановка приводит к новому состоянию.
Если перестановка происходит в одном и том же состоянии, то она тождественная и выбрасывается из рассмотрения. Для бозонов из N! перестановок  тождественные перестановки. Тогда надо рассматривать
тождественные перестановки. Тогда надо рассматривать  перестановок, где N всего бозонов, а в 1-ом состоянии находится N1 частиц, во 2-ом N2 частиц и тд.
перестановок, где N всего бозонов, а в 1-ом состоянии находится N1 частиц, во 2-ом N2 частиц и тд.

Симметричные состояния допускают произвольное число частиц в одночастичном состоянии.
|
|
|
Тогда нормировочный множитель

2. Рассмотрим антисимметричные состояния
Здесь
 (51.3)
(51.3)

Чтобы учесть знак вводят понятие парной (соседней, элементарной) перестановки.
Пусть надо переставить в ряде  цифры 1 и 4. Учтем элементарные перестановки:
цифры 1 и 4. Учтем элементарные перестановки:
2134, 2314, и т. д.
Здесь 5 элементарных перестановок.  .
.
Тогда в сумму (51.3) надо поставить  .
.

Если i и j в одном состоянии, то  ,
,  =>
=>  .
.
Антисимметричные состояния запрещают нахождение более одной частицы в одночастичном состоянии.
В сумме (51.3) оператор  это оператор не элементарной перестановки, а какой-то конкретной перестановки.
это оператор не элементарной перестановки, а какой-то конкретной перестановки.
Итак получаем из (51.3) выражение

Рассмотрим пару частиц, тогда

Эта функция обладает свойством антисимметричности. Подействуем на нее оператором перестановки:
 ,
,
т. е.
 - собственная функция оператора перестановки.
- собственная функция оператора перестановки.
Здесь 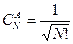 т. к. у фермионов в каждом одночастичном состоянии число частиц не превышает 1, т. е. 0 или 1.
т. к. у фермионов в каждом одночастичном состоянии число частиц не превышает 1, т. е. 0 или 1.
В наиболее общем виде
 .
.
Обобщим

Из этого вида вытекает принцип Паули: не более одного фермиона может находиться в одном квантовом состоянии.
Допустим две частицы в одном квантовом состоянии, тогда у них совпадают квантовые числа, т. е.  . Тогда для детерминанта имеем 2 одинаковые строки, он равен нулю. Состояние не реализуется.
. Тогда для детерминанта имеем 2 одинаковые строки, он равен нулю. Состояние не реализуется.
Решения задач по курсу "Квантовая теория".
Задача 1. Рассмотреть следующие операторы 
а) инверсии  ;
;
б) трансляции  ;
;
в) изменения масштаба  ;
;
г) комплексного сопряжения  .
.
Решение. Представим  в форме
в форме
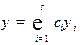 , где
, где  и
и  . (1.1)
. (1.1)
Учтем, что соотношения а-г (см. условие задачи) справедливы для каждой из функций  , входящих в суперпозицию (1.1). Тогда имеем:
, входящих в суперпозицию (1.1). Тогда имеем:
а) 
 ;
;
б) 
 ;
;
в) 
 ;
;
г) 

Таким образом, лишь последний из рассмотренных операторов не удовлетворяет свойству линейности.
Задача 2. Используя свойства
1.  ; (2.1)
; (2.1)
2. 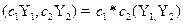 ; (2.2)
; (2.2)
3. 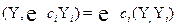 (2.3)
(2.3)
скалярного произведения
 ,
,  . (2.4)
. (2.4)
Доказать неравенство Коши-Шварца-Буняковского
|
|
|
 . (2.5)
. (2.5)
Решение. Запишем норму функции 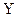 вида
вида
 , где
, где  -вещественное число
-вещественное число 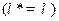 .
.
Тогда из  с учетом (2.1)-(2.3) найдем
с учетом (2.1)-(2.3) найдем

 .
.
Ввиду произвольности  положительность нормы
положительность нормы  достигается при условии неположительности дискриминанта
достигается при условии неположительности дискриминанта
 ,
,
поставленного в соответствие неравенству  . Легко видеть, что из
. Легко видеть, что из  автоматически следует неравенство (2.5). Знак равенства в формуле (2.5) имеет место в том и только в том случае, когда функция
автоматически следует неравенство (2.5). Знак равенства в формуле (2.5) имеет место в том и только в том случае, когда функция  и
и  пропорциональны друг другу, т.е.
пропорциональны друг другу, т.е.
 ,
,  .
.
Задача 3. Найти оператор  , если
, если
а)  ,
,  ;
;  ,
,  ;
;
б)  ,
,  ;
;  ,
,  .
.
Решение. Подставляя явный вид  в правую часть
в правую часть  и проводя интегрирование по частям, получим
и проводя интегрирование по частям, получим
а)  ,
,

б)  ,
,
 .
.
Здесь использовано обращение функций  и
и  в нуль на бесконечности в случае (а) и условие периодичности функции
в нуль на бесконечности в случае (а) и условие периодичности функции  и
и  в случае (б). В обоих случаях оператор
в случае (б). В обоих случаях оператор  не совпадает с оператором
не совпадает с оператором  .
.
Задача 4. Показать, что произвольный линейный оператор  может быть представлен в виде
может быть представлен в виде
 ;
;  ,
,  .
.
Решение. Легко видеть, что справедливо разложение  на сумму
на сумму

двух операторов, первый из которых является эрмитовым:
 ,
,  ,
,
а второй – антиэрмитовым:
 .
.
С их помощью будем иметь
 ;
;  ,
,  ;
;
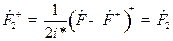 ,
,  .
.
Всякая линейная комбинация эрмитовых операторов с вещественными коэффициентами есть Эрмитов оператор. Произведение двух эрмитовых операторов не обязательно эрмитово.
Задача 5. Найти  , если
, если  - произведение эрмитовых операторов
- произведение эрмитовых операторов  и
и 
Решение. Из определения  имеем
имеем
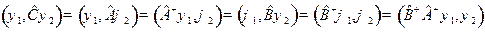 ;
;
 ,
,  /
/
Отсюда с учетом эрмитовости  и
и  найдем
найдем
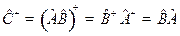 . (5.1)
. (5.1)
Легко видеть, что в общем случае  .
.
Задача 6. Показать, что при условии эрмитовости  и
и  операторы
операторы  и
и  , также эрмитовы.
, также эрмитовы.
Решение. Из решения задач 4 и 5 следует, что линейному оператору  можно поставить в соответствие два самосопряженных оператора:
можно поставить в соответствие два самосопряженных оператора:
 ;
; 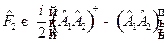
Эрмитовость операторов  ,
,  и равенство (5.1) приводят к эрмитовости операторов
и равенство (5.1) приводят к эрмитовости операторов  и
и  :
:
 ;
;  .
.
Задача 7. Используя определение  (7.1) и свойство
(7.1) и свойство  (7.2), показать, что уравнение
(7.2), показать, что уравнение  (7.3) имеет решение лишь для вещественного числа
(7.3) имеет решение лишь для вещественного числа  .
.
Решение. Подставляя
 ,
,
где  - решение уравнения (7.3), в определение эрмитова оператора (7.1), запишем
- решение уравнения (7.3), в определение эрмитова оператора (7.1), запишем
 .
.
Используя свойство (7.2), вынесем число  , стоящее слева и справа от запятой, за знак скалярного произведения. Это дает
, стоящее слева и справа от запятой, за знак скалярного произведения. Это дает
 .
.
Сокращая на положительное число  , получим
, получим
 .
.
Задача 8. Доказать, что собственные функции эрмитова оператора  с невырожденным дискретным спектром ортогональны.
с невырожденным дискретным спектром ортогональны.
|
|
|
Решение. В качестве функции  и
и  в определении
в определении  рассмотрим
рассмотрим  и
и  , являющиеся решениями уравнений
, являющиеся решениями уравнений
 ,
,  (8.1)
(8.1)
соответственно. Воспользуемся определением (7.1) эрмитова оператора, записав его в форме  .
.
Подставляя сюда правые части уравнений (8.1) и учитывая свойство (7.2), получим
 .
.
В силу вещественности и невырожденности собственных значений  и
и  , отсюда найдем
, отсюда найдем
 ;
; 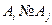 ,
,  , (8.2)
, (8.2)
что и требовалось доказать.
Объединяя равенства  (8.4) и (8.2), запишем условие ортонормированности
(8.4) и (8.2), запишем условие ортонормированности
 (8.3)
(8.3)
собственных функций эрмитова оператора с невырожденным дискретным спектром.
Задача 9. Используя свойство ортонормированности (8.2), найти коэффициенты  разложения произвольной функции
разложения произвольной функции  по базису в гильбертовом пространстве.
по базису в гильбертовом пространстве.
Решение. В качестве базиса выберем собственные функции оператора  , полученные решением уравнения (7.3) и удовлетворяющие условию (8.3). Искомое разложение представим в форме
, полученные решением уравнения (7.3) и удовлетворяющие условию (8.3). Искомое разложение представим в форме
 ,
,
где суммирование проводится по всем значениям индекса  (т.е по всем собственным значениям
(т.е по всем собственным значениям  оператора
оператора  ). Для нахождения коэффициентов
). Для нахождения коэффициентов  запишем скалярное произведение
запишем скалярное произведение
 .
.
Преобразуем его с учетом свойств (7.2),  , (8.3). Это дает
, (8.3). Это дает

Таким образом, окончательно запишем
 ,
,  .
.
Коэффициент  имеет смысл проекции функции
имеет смысл проекции функции  на орт
на орт  гильбертова пространства.
гильбертова пространства.
Задача 10. Решить уравнение (7.3) для оператора
 ,
, 
Решение. Из решения задачи 3б и равенств  (10.1) найдем
(10.1) найдем
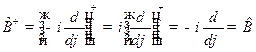 ,
,
т.е. рассматриваемый оператор  Эрмитов, а его собственные значения вещественны. Уравнение (7.3) примет вид
Эрмитов, а его собственные значения вещественны. Уравнение (7.3) примет вид
 .
.
Решая его, найдем
 .
.
Из условия периодичности (см. задачу 3б)
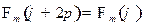
вытекает равенство
 ,
,
из которого получаем ограничение
 ;
; 
Из дискретности и невырожденности спектра следует, что после нормировки (8.4) функции  будут обладать свойством (8.3).
будут обладать свойством (8.3).
Запишем условие нормировки (8.4) в виде

В общем случае постоянный множитель есть комплексное число. однако ввиду всегда допустимого введения произвольного фазового множителя
 ,
,  (10.1)
(10.1)
будем предполагать вещественность константы  . Это дает
. Это дает

Окончательно запишем
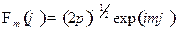 ;
; 
Задача 11. Решить уравнение (7.3) для оператора
|
|
|
 ,
,  .
.
Решение. Из (10.1) и решения задачи 3а следует, что рассматриваемый оператор Эрмитов. Следовательно, его собственные значения вещественны. Уравнение (7.3) примет вид
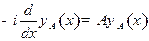 ,
, 
Решая его, найдем
 . (11.1)
. (11.1)
Норма функции  неограниченна, поскольку
неограниченна, поскольку
 .
.
Следовательно, при соответствующем выборе константы  функции
функции  и
и 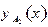 вида (11.1) будут удовлетворять условию
вида (11.1) будут удовлетворять условию  (11.2).
(11.2).
Для расчета  воспользуемся равенством
воспользуемся равенством 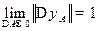 . Собственный дифференциал
. Собственный дифференциал  для функции (11.1) имеет вид
для функции (11.1) имеет вид

 .
.
Подставляя  в определение нормы
в определение нормы  (11.3), приходим к интегралу
(11.3), приходим к интегралу

который после замены переменных

приводя к виду

Используя табличный интеграл
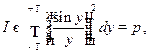
из условия нормировки получим

Как и в задаче 10, константу нормировки  выберем вещественной. Таким образом, окончательно запишем
выберем вещественной. Таким образом, окончательно запишем
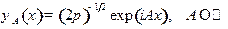 . (11.4)
. (11.4)
Задача 12. Для стационарного состояния вида
 (12.1)
(12.1)
описывающего в одномерном случае частицу в бесконечно глубокой потенциальной яме ширины  , рассчитать средние значения величин, соответствующих операторам:
, рассчитать средние значения величин, соответствующих операторам:
а) 
б) 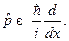
Решение. а) По определению 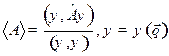 (12.2), запишем
(12.2), запишем
 (12.3)
(12.3)
Расчет числителя (12.3) дает

где использованы соотношения

Аналогичным образом для знаменателя (12.3) получим

Следовательно, для 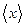 будем иметь
будем иметь

б) Учитывая свойство (7.2) и определение (12.2), запишем
 . (12.4)
. (12.4)
Расчет числителя (12.4) дает


таким образом, для  будем иметь
будем иметь

Задача 13. В  - представлении решить уравнение
- представлении решить уравнение  (13.1) для оператора
(13.1) для оператора  .
.
Решение. В одном случае имеем
 (13.2)
(13.2)
где  - некоторое собственное значение оператора
- некоторое собственное значение оператора  . Учитывая определения
. Учитывая определения
 (13.6)
(13.6)
отсюда найдем
 (13.3)
(13.3)
Равенство (13.3) возможно лишь при условии, что  равна нулю всюду, кроме точки
равна нулю всюду, кроме точки  . Среди решений уравнения (13.2) или (13.3) не существует ни одной квадратично-интегрируемой функции. Единственной функцией, удовлетворяющей (13.2) и нормировке (11.2), является дельта-функция, определенная равенствами
. Среди решений уравнения (13.2) или (13.3) не существует ни одной квадратично-интегрируемой функции. Единственной функцией, удовлетворяющей (13.2) и нормировке (11.2), является дельта-функция, определенная равенствами
 , (13.4)
, (13.4)
 . (13.5)
. (13.5)
Таким образом, функция  имеет вид
имеет вид
 .
.
В трехмерном случае вместо (13.2) запишем
 . (13.7).
. (13.7).
В силу (13.6) оператор 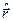 представим в виде суммы трех коммутативных операторов:
представим в виде суммы трех коммутативных операторов:  . Это обстоятельство позволяет для решения уравнения (13.7) использовать метод разделения переменны. Это дает
. Это обстоятельство позволяет для решения уравнения (13.7) использовать метод разделения переменны. Это дает
 (13.8)
(13.8)
Решая (13.8) и учитывая равенство
 (13.9)
(13.9)
вытекающее из определения дельта-функции в 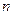 - мерном пространстве векторов
- мерном пространстве векторов 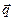 :
:
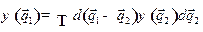 , (13.10)
, (13.10)
для  найдем
найдем
 .
.
Задача 14. В  - представлении найти собственную функцию оператора импульса.
- представлении найти собственную функцию оператора импульса.
Решение. Записывая  (14.1) в декартовых координатах
(14.1) в декартовых координатах
 (14.2)
(14.2)
и учитывая, что  представим в форме суммы трех коммутативных операторов (так же, как и
представим в форме суммы трех коммутативных операторов (так же, как и 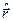 ),
),
 (14.3)
(14.3)
воспользуемся решением сходной одномерной задачи II. Уравнение (13.1) в обозначениях (14.3) принимает вид
 (14.4)
(14.4)
Уравнения (14.4) сводятся к трем одномерным уравнениям 
|
|
|

подобным исследованному в задаче II. Из (11.4) имеем
 (14.5)
(14.5)
Вещественная, как и в (11.4), константа  находится из условия нормировки (11.2)
находится из условия нормировки (11.2)
 (14.6)
(14.6)
Подставляя (14.5) в (14.6)

и проводя под интегралом замену переменных  , найдем
, найдем

что с учетом (13.5) дает

Подставляя найденную константу  в (14.5) получим
в (14.5) получим

что вместе с (14.4) дает
 (14.7)
(14.7)
Условие ортонормированности (11.2) для собственной функции (14.7) оператора импульса с учетом (13.9) и (14.6) имеет вид
 (14.8)
(14.8)
Здесь индексами 1 и 2 нумеруются различные значения 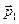 и
и  вектора
вектора  , тогда как в (14.4) эти же индексы используются для обозначения проекций
, тогда как в (14.4) эти же индексы используются для обозначения проекций  и
и  вектора
вектора  на соответствующие оси декартовых координат.
на соответствующие оси декартовых координат.
Задача 15. В  - представлении получить явный вид оператора
- представлении получить явный вид оператора  , используя координаты а) декартовы; б) сферические.
, используя координаты а) декартовы; б) сферические.
Решение. а) В декартовых координатах (14.3) и (14.2) имеем
 (15.1)
(15.1)
б) Переход от декартовых координат 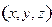 к сферическим
к сферическим  определяется формулами:
определяется формулами:
 (15.2)
(15.2)
 (15.3)
(15.3)
Для операторов  и
и 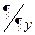 переход (15.2) к сферическим координатам дает
переход (15.2) к сферическим координатам дает

Подставляя эти выражения в (15.1), запишем
 (15.4)
(15.4)
С учетом (15.3) произведенные сферических координат и выражения в круглых скобках (15.4) приводятся к виду
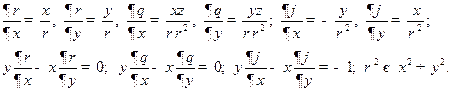 (15.5)
(15.5)
Подставляя вторую строку (15.5) в (15.4), для оператора  в сферических координатах получаем
в сферических координатах получаем
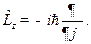 (15.6)
(15.6)
Задача 16. В сферических координатах  - представления найти собственную функцию оператора
- представления найти собственную функцию оператора  .
.
Решение. Оператор  (15.6)связан с оператором
(15.6)связан с оператором  задачи 10 равенством
задачи 10 равенством

Используя решение задачи 10, для собственных функций  , удовлетворяющих уравнению
, удовлетворяющих уравнению
 (16.1)
(16.1)
(где  - собственное значение оператора
- собственное значение оператора  , соответствующее
, соответствующее  ), получаем
), получаем
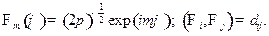 (16.2)
(16.2)
Задача 17. В  - представлении (одномерная система) решить уравнение (7.3) для оператора
- представлении (одномерная система) решить уравнение (7.3) для оператора 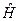 в случае частицы в бесконечно глубокой потенциальной яме, ширины
в случае частицы в бесконечно глубокой потенциальной яме, ширины  .
.
Решение. В случае бесконечно глубокой ямы по определению имеем
 (17.1)
(17.1)
Интересующее нас решение ищем на отрезке  (17.2)
(17.2)
Поскольку в точках  и
и  потенциальная энергия частицы обращается в бесконечность, вероятность преодоления бесконечного барьера и попадания за пределы области (17.2) равна нулю. Оказавшись в области (17.2), частица все время будет находиться в ней. Из формул
потенциальная энергия частицы обращается в бесконечность, вероятность преодоления бесконечного барьера и попадания за пределы области (17.2) равна нулю. Оказавшись в области (17.2), частица все время будет находиться в ней. Из формул  (17.3) и
(17.3) и

(17.4) следуют соотношения

где  - волновая функция
- волновая функция  , удовлетворяющая стационарному уравнению Шредингера
, удовлетворяющая стационарному уравнению Шредингера
 (17.5)
(17.5)
совпадающему с уравнением (13.1) или (13.2) (в зависимости от характера спектра), т.е. функция  , удовлетворяющая (17.5), есть собственная функция
, удовлетворяющая (17.5), есть собственная функция 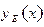 оператора
оператора 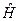 , соответствующая собственному значению
, соответствующая собственному значению  . Из сказанного вытекают граничные условия
. Из сказанного вытекают граничные условия  , накладываемые на решение уравнения (17.5).
, накладываемые на решение уравнения (17.5).
Таким образом, приходим к задаче
 (17.6)
(17.6)
Отсюда следует:
 (17.7)
(17.7)
Положительность собственного значения  оператора
оператора 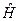 вытекает из положительности
вытекает из положительности  и
и  . Решение уравнения (17.7) представимо в виде суперпозиции двух элементарных состояний, которые на языке
. Решение уравнения (17.7) представимо в виде суперпозиции двух элементарных состояний, которые на языке  (17.3) интерпретируются как волны де Броля, распространяющиеся в противоположных направлениях оси
(17.3) интерпретируются как волны де Броля, распространяющиеся в противоположных направлениях оси  :
:
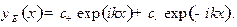 (17.8)
(17.8)
Подстановка (17.8) в граничные условия (17.6) приводит к системе однородных уравнений
 (17.9)
(17.9)
для неизвестных коэффициентов  . Критерий существования етривиального решения этой системы
. Критерий существования етривиального решения этой системы

дает условие квантования

собственного значения  (17.5). Это означает, что
(17.5). Это означает, что 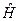 обладает дискретным спектром, а уравнение (17.5) эквивалентно (7.3). Вводя согласно (17.9) обозначения
обладает дискретным спектром, а уравнение (17.5) эквивалентно (7.3). Вводя согласно (17.9) обозначения
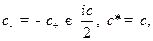
где  - пока неизвестная вещественная (в силу наличия у
- пока неизвестная вещественная (в силу наличия у  произвольного фазового множителя (10.1) это всегда возможно) константа, для функции (17.8) будем иметь
произвольного фазового множителя (10.1) это всегда возможно) константа, для функции (17.8) будем иметь
 (17.10)
(17.10)
Поскольку собственные функции оператора 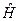 с дискретным спектром квадратично интегрируемы, условие нормировки имеет вид
с дискретным спектром квадратично интегрируемы, условие нормировки имеет вид

Отсюда с учетом решения задачи 12 находим
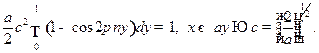
Подставляя найденное значение константы в (17.10), запишем решение задачи в окончательной форме
 (17.11)
(17.11)
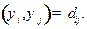
Задача 18. Используя формулы (17.4) и решения задач 13 и 14, найти плотности вероятностей  и
и 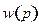 для стационарного состояния
для стационарного состояния  (см. задачу 17).
(см. задачу 17).
Решение. а) Согласно (17.3) амплитуда  разложения состояния
разложения состояния  по базису
по базису  равна
равна
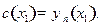
В силу нормировки  на единицу из (17.4) и (17.11) найдем
на единицу из (17.4) и (17.11) найдем

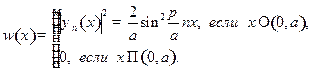 (18.1)
(18.1)
б) Аналогично  (18.2) для амплитуды
(18.2) для амплитуды  разложения
разложения  по базису
по базису  запишем
запишем

Подставляя сюда  из (17.11), вводя обозначения
из (17.11), вводя обозначения

и проводя интегрирование, получим
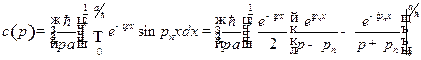 .
.
Учитывая равенства

для  в (17.4) будем иметь
в (17.4) будем иметь

Подставляя  в (17.4), запишем
в (17.4), запишем
 (18.3)
(18.3)
Условие нормировки в (18.3) вытекает из равенства Парсеваля в форме

справедливой в случае непрерывного спектра собственных значений 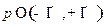 оператора
оператора  .
.
Задача 19. Рассчитать коммутатор  .
.
Решение. Для нахождения явного вида оператора  необходимо рассмотреть результат его действия на произвольную функцию
необходимо рассмотреть результат его действия на произвольную функцию  . Используя (13.6), (14.2) и определение
. Используя (13.6), (14.2) и определение  (19.1), запишем
(19.1), запишем

 . (19.2)
. (19.2)
Задача 20. Найти коммутатор  .
.
Решение. Используя (19.2) и вид  в
в  - представлении
- представлении 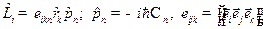 (20.1), запишем
(20.1), запишем
 . (20.2)
. (20.2)
Задача 21. Показать, что  .
.
Решение. Воспользуемся соотношением
 , (21.1)
, (21.1)
легко проверяемым непосредственной подстановкой всех коммутаторов в (21.1) согласно определению (19.1).
Тогда для искомого коммутатора запишем
 . (21.2)
. (21.2)
Ввиду симметричности (относительно перестановки индексов) оператора  и антисимметричности (согласно определению (20.1)) тензора
и антисимметричности (согласно определению (20.1)) тензора  двойное суммирование в (21.2) по индексам
двойное суммирование в (21.2) по индексам  и
и  дает нуль. Равенство
дает нуль. Равенство
 (21.3)
(21.3)
объясняется также и тем, что скалярный оператор инвариантен относительно преобразования
 . (21.4)
. (21.4)
Задача 22. Используя неравенство Коши-Шварца-Буняковского получить нижнюю границу для дисперсии  наблюдаемой
наблюдаемой  .
.
Решение. Выбирая в качестве  и
и  функции
функции

и используя неравенство
 , (22.1)
, (22.1)
получим
 . (22.2)
. (22.2)
В силу эрмитовости  оператор
оператор  так же эрмитов (7.1), т.е. выполняется равенство
так же эрмитов (7.1), т.е. выполняется равенство
 . (22.3)
. (22.3)
Согласно определению (13.5) неравенство (22.2) принимает вид
 .
.
Отсюда с учетом
 (22.4)
(22.4)
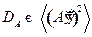 (22.5)
(22.5)
получим
 .
.
Таким образом, мы нашли, что наименьшее из возможных значений дисперсии  (и среднеквадратичного отклонения
(и среднеквадратичного отклонения 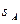 ) физической величины
) физической величины  равно нулю.
равно нулю.
Задача 23. Доказать, что  обращается в нуль, если соотношение, по которому проводится усреднение, описывается собственной функцией оператора
обращается в нуль, если соотношение, по которому проводится усреднение, описывается собственной функцией оператора  .
.
Решение. Пусть в качестве  в (13.5) выбрана
в (13.5) выбрана  , удовлетворяющая (7.3). Тогда в силу
, удовлетворяющая (7.3). Тогда в силу
 , (23.1)
, (23.1)
 (23.2)
(23.2)
и (13.5) запишем
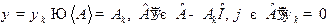 .
.
С учетом определения (22.5) и равенства (22.3) это дает
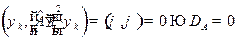 .
.
Верно и обратное: равенство нулю нормы некоторой функции
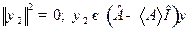
реализуется лишь в случае равенства нулю этой функции:
 . (23.3)
. (23.3)
Сравнивая равенство (23.3) с уравнением (7.3), заключаем, что оно возможно, если  - одна из собственных функций оператора
- одна из собственных функций оператора 
 ,
,
где  - собственное значение оператора
- собственное значение оператора  , соответствующее этой собственной функции.
, соответствующее этой собственной функции.
Задача 24. Для стационарного состояния (17.11) рассчитать  и
и 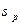 (см. задачу 12).
(см. задачу 12).
Решение. Согласно определению  (24.1) запишем
(24.1) запишем
 . (24.2)
. (24.2)
Для получения  и
и 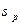 (с учетом
(с учетом  (24.3) и
(24.3) и  (24.4) нам остается рассчитать
(24.4) нам остается рассчитать  и
и  . По определению (13.5) для
. По определению (13.5) для  имеем
имеем
 . (24.5)
. (24.5)
а) В случае  число
число  находится вычислениями
находится вычислениями

 ,
,
подобными проделанным в задаче 12а. Следовательно,
 . (24.6)
. (24.6)
Подставляя (24.6) и (24.3) в (24.2), получим
 . (24.7)
. (24.7)
б) Для оператора  (см. задачу 12б) найдем
(см. задачу 12б) найдем
 .(27.8)
.(27.8)
Подстановка (24.8) и (24.4) в (24.2) дает
 . (24.9)
. (24.9)
Решения дополнительных задач по курсу "Квантовая теория".
1. Доказать соотношение:

Решение.
Введём оператор  и разложим его в ряд Тейлора в точке
и разложим его в ряд Тейлора в точке  :
:
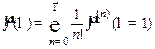
При этом
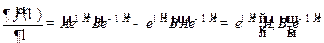
Аналогично находим производные более высокого порядка:
 и т.д.
и т.д.
Тогда

2. В состоянии частицы с волновой функцией  , где
, где  ,
, 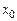 , a-вещественные параметры, найти распределение вероятностей различных значений координаты. Определить средние значения координаты
, a-вещественные параметры, найти распределение вероятностей различных значений координаты. Определить средние значения координаты


