 |
Дополнительные задачи по курсу “Квантовая теория”.
|
|
|
|
1. Доказать соотношение:
2. В состоянии частицы с волновой функцией 
, где 
, 
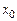, a-вещественные параметры, найти распределение вероятностей различных значений координаты. Определить средние значения координаты 
и импульса 
частицы, а также средние значения их квадратов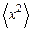 
, 
. Показать, что такая в.ф. минимизирует соотношение неопределённостей: 
. Состояния, минимизирующие соотношение неопределённостей, называются когерентными.
3. Найти собственные функции и собственные значения физической величины, представляющей линейную комбинацию одноименных компонент импульса и координаты частицы: 
. Убедиться в ортогональности полученных функций и нормировать их соответствующим образом.
4. Найти уровни энергии и нормированные волновые функции состояний дискретного спектра частицы в 
-потенциале, 
. Найти средние значения кинетической и потенциальной энергии в этих состояниях. Вычислить произведение неопределенностей координаты и импульса. Каков вид волновой функции в импульсном представлении?
5. Найти связанные состояния и соответствующие им собственные значения в случае прямоугольной потенциальной ямы
6. Найти значения энергий, при которых частицы не отражаются от потенциального барьера вида 
.
7. Для частицы в периодическом потенциале вида 
(идеальный бесконечный «кристалл», см. рис. 1) найти систему независимых решений уравнения Шрёдингера для произвольного значения E. Определить энергетический спектр частицы.
8. Найти сдвиг в слабом электрическом поле и поляризуемость основного уровня
заряженной частицы в одномерном -потенциале 
.
9. 1) Найти собственные функции и собственные значения операторов рождения и уничтожения. В рассматриваемых состояниях найти распределение по числу частиц. Обсудить случаи бозонных и фермионных операторов. 2) Показать, что применительно к линейному осциллятору собственные функции оператора 
описывают когерентные состояния.
|
|
|
10. Состояние свободной частицы при t = 0 описывается волновой функцией
Найти изменение во времени и следующие средние: 
.
11. Найти унитарный оператор, соответствующий преобразованию Галилея, т.е. переходу в новую инерциальную системы отсчета. Убедиться в инвариантности уравнения Шрёдингера относительно этого преобразования. Как при этом преобразуется волновая функция частицы в координатном и импульсном представлениях?
12. Найти унитарный оператор, соответствующий калибровочному преобразованию потенциалов электромагнитного поля. Убедиться в инвариантности уравнения Шредингера относительно этого преобразования.
13. Исследовать энергетический спектр поперечного движения заряженной бесспиновой частицы в однородном магнитном поле, введя соответствующим образом выбранные операторы рождения и уничтожения. Воспользоваться выражением 
для векторного потенциала.
[1] + и – соответствуют чётным и нечётным решениям.
[2] В силу того, что потенциал трансляционно инвариантен (периодичен), в.ф. в соседней ячейке (n+1) может отличаться от в.ф. в предыдущей ячейке n лишь порстоянным множителем, что мы и отразили в (2). При этом ясно, что по модулю он равен 1.
[3] В данном случае основным состоянием будет состояние с отрицательной энергией, соответствующее - яме. Ближайшее энергетическое состояние E=0 уже принадлежит непрерывному спектру. Поэтому при вычислении поправок к энергии по теории возмущений вместо сумм надо брать интегралы.
[4] и есть искомое значение поляризуемости, по определению.
|
|
|
