 |
Уравнение Шредингера в матричной форме.
|
|
|
|
Уравнение Шредингера:
переходит в следующее:
,
-матричные элементы оператора энергий.
Здесь существует нюанс: оператор 
в энергетическом представлении должен быть стационарным, т.е. 
, тогда удается решить задачу
, (38.1)
иначе эта задача имеет сложное решение, т.к. там уже 
.
Для случая и 
, тогда имеем (*)
Решая (38.1), имеем
.
Очень часто рассматривается представление в котором энергия диагональна и рассматривается переход от Шредингеровского к Гайзенберговскому описанию. Т.е. у операторов есть временная зависимость и еще мы рассматриваем энергетическое представление, т.е.
.
- переносит временную зависимость на оператор.
- переводит к энергетическому представлению.
Здесь действует фактически один оператор:
.
Тогда оператор
.
,
т.к. операторы и действуют на различные переменные, то они коммутативны, т.е.
,
тогда
,
.
Но мы знаем, что оператор 
сводится к матрице
{оператор (для стационарных : ) : 
}= 
{ 
, т.к. - унитарный оператор, тогда 
}= 
= 
{вводится частота 
}= 
.
Тогда в энергетическом представлении:
Мы получили заготовку для решения задачи о линейном гармоническом осцилляторе.
Для представления Гайзенберга справедливо соотношение:
Уравнение движения
.
Это некое уравнение движения.
Рассмотрим
.
§ 34*. Матричная формулировка задачи о линейном гармоническом осцилляторе.
Запишем Гамильтониан для линейного гармонического осциллятора (ЛГО):
Классическая функция для ЛГО:
.
В квантовой механике – оператор ЛГО:
.
Удобно ввести безразмерный оператор энергии:
,
тогда
.
Здесь можно ввести безразмерную координату, т.к. эта величина тоже безразмерная.
.
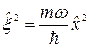Тогда оператор
,
где
- безразмерный импульс.
|
|
|
Тогда
,
.
Теперь запишем уравнение движения в Гайзенберговском представлении
,
т.к. 
явно от времени не зависит.
.
Мы знаем, что
,
.
Дифференцируя, имеем:
.
Тогда
(39.1)
Найдем
.
Тогда имеем
.
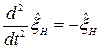Это уравнение движения ЛГО в квантовой механике.
В классической механике
,
А в квантовой
. (39.2)
Если рассмотрим
,
тогда
(39.3)
Из (39.1) и (39.3) имеем
(39.4)
Запишем уравнения (39.2) и (39.4) в матричной форме.
.
.
Переводим в матричную форму
. (39.5)
Т. к.
, то
.
Тогда из (39.5) имеем
.
(39.6)
Имеем уравнение движения
.
Посмотрим при каких условиях оно имеет решение
.
Получили дисперсионное уравнение.
Нетривиальное его решение имеет место, если
.
.
Отсюда, примем
.
Получили решение дисперсионного уравнения.
§ 35*. Расчет матричных элементов операторов 
.
Имеют место отличные от нуля матричные элементы.
.
Установим связь между 
и 
.
Т. к. 
(40.1)
В матричной форме
. (40.2)
Подставляя (40.2) в (40.1), имеем
.
Так как оператор координаты вещественный, то
.
Матрица координат симметричная относительно главной диагонали.
Рассмотрим матричную форму (6*) из предыдущего параграфа и учтем, что в нем только при 
существуют ненулевые слагаемые.
Рассмотрим случай 
и учтем, что 
.
,
тогда
,
учтем, что 
и 
, тогда
.
Так как задача одномерная, то номер состояния будет совпадать с номером энергетического уровня.
Рассмотрим основное состояние 
.
.
,
т.к. таких состояний нет, тогда
.
Рассмотрим 
,
но
,
тогда
,
и т.д.
Для любого 
:
,
.
Можно записать матричные элементы оператора координаты в общем виде:
.
Найдем матричные элементы для оператора импульса 
.
Было получено
.
,
оператор - чисто мнимый.
Для оператора импульса получаем антисимметричную матрицу.
.
Итак
.
Для оператора 
матричные элементы имеют вид
.
Получили диагональную матрицу. Тогда
.
Основное состояние: 
описывается в координатном представлении 
, и в энергетическом представлении через 
.
|
|
|
Имеем энергию нулевых колебаний:
.
- описывается полиномами Эрмита, например
.
Плотность вероятности для координаты в основном состоянии:
.
|
|
|
