 |
3. 2. Теплоотдача при вынужденном
|
|
|
|
3. 2. ТЕПЛООТДАЧА ПРИ ВЫНУЖДЕННОМ
ДВИЖЕНИИ ТЕПЛОНОСИТЕЛЯ
3. 2. 1. ТЕПЛООТДАЧА ПРИ ТЕЧЕНИИ
ЖИДКОСТИ (ГАЗА) В ТРУБАХ
Расчет теплоотдачи при движении жидкости (газа) в трубах представляет особый интерес, так как трубчатые аппараты и теплооб-менники нашли самое широкое распространение в теплотехнологиях различных производств.
Различают два режима движения теплоносителя в трубах - ламинарный и турбулентный. О режиме течения судят по величине числа Рейнольдса. В ламинарной области течения при скоростях, соответствующих значению критического числа Рейнольдса Re ≤ 2300, теплота передается теплопроводностью по нормали к общему направ-лению движения потока. Конвективная составляющая теплоотдачи будет больше или меньше в соответствии с распределением скоростей по сечению потока. При значительной разности температур в потоке возникает, как следствие, разность плотностей. На вынужденное дви-жение накладывается свободное движение, турбулизирующее поток, и теплообмен интенсифицируется. Влияние свободной конвекции заметно при Gr∙ Pr > 8∙ 105. Ламинарное течение в отсутствие свободной конвек-ции принято называть вязкостным, а течение, сопровождающееся свободной конвекцией, - вязкостно-гравитационным. Вязкостный ре-жим тем более вероятен, чем больше вязкость жидкости и меньше диаметр трубы и температурный напор.
С ростом скорости ламинарное движение все более разрушается. При Re ≥ 104 устанавливается устойчивый турбулентрый режим. Возникает перемешивание, интенсифицирующее конвективный теплообмен. Теп-лота передается теплопроводностью лишь в очень тонком ламинарном подслое, откуда она передается в глубь потока конвекцией (хаотически движущимися частицами жидкости). Режим течения, соответствующий значениям числа Рейнольдса 2300< Re< 104, называ-ется переходным. В этом случае в потоке могут сосуществовать ламинарная и турбулентная области.
|
|
|
При ламинарном изотермическом течении жидкости внутри технически гладкой трубы устанавливается параболический профиль скоростей (рис. 3. 3, а). Средняя скорость теплоносителя при этом составляет w = 0, 5 wмакс. В условиях теплообмена даже в отсутствие влияния свободной конвекции распределение скорости по сечению трубы может значительно отличаться от профиля скорости изотерми-ческого потока, если вязкость теплоносителя заметно изменяется с изменением тем пературы.
При турбулентном режиме движения жидкости (газа) распределение скорости по поперечному сечению трубы имеет пологий характер усеченной параболы (рис. 3. 3, б). Средняя скорость теплоносителя при турбулентном изотермическом течении w ≈ (0, 8 -0, 9) wмакс. Следует иметь в виду, что отмеченная закономерность турбулентного течения жидкости справедлива только при изотермическом течении.

Рис. 3. 3. Распределение скоростей по поперечному сечению при
ламинарном (а) и турбулентном (б) режимах течения жидкости в
трубе: 1 – ламинарный поток; 2 – эпюры (профили) скоростей;
3 – турбулентное ядро; 4 – пристенный слой
Как в случае ламинарного, так и в случае турбулентного движения стабилизация потока с характерным для этих режимов распределением скоростей по сечению наступает не сразу при входе потока в трубу. Если теплоноситель поступает в трубу из большого объема и стенки трубы на входе закруглены, то распределение скоростей на входе будет прямолинейным, а эпюра скоростей имеет вид прямоугольника. Под действием сил вязкостного трения образуется ламинарный пограничный слой, толщина которого растет по мере удаления от входного сечения и затем пограничные слои сливаются (рис. 3. 4, а). При турбулентном режиме течения ламинарный слой разрушается и переходит в турбулентный пограничный слой с вязким подслоем. После смыкания пограничных слоев течение приобретает стабилизированный турбулентный характер (рис. 3. 4, б). Расстояние от входа в трубу до сечения, в котором динамические пограничные слои смыкаются,
|
|
|

Рис. 3. 4. Гидродинамическая стабилизация потока в трубе при
ламинарном (а) и турбулентном (б) течениях.
называется гидродинамическим начальным участком, или участком гидродинамической стабилизации
При ламинарном течении теплоносителя в трубе круглого сечения c внутренним диаметром d длина гидродинамического начального участка определяется по формуле:
ℓ г = 0, 065·d·Re, (3. 28)
и при турбулентном режиме
ℓ г = 15d. (3. 29)
Аналогично начальному участку гидродинамической стабилизации существует тепловой начальный участок или участок тепловой стабилизации ℓ т. Качественный характер деформации эпюры температур на начальном участке тепловой стабилизации показан на рис. 3. 5.
Длина участка тепловой стабилизации при постоянной температуре стенки, постоянных физических параметрах теплоносителя и ламинар-ном режиме движения равна:
ℓ т = 0, 055·d·Re·Pr (3. 30)

Рис. 3. 5. Начальный участок тепловой стабилизации
при турбулентном режиме движения теплоносителя
и при турбулентном режиме
ℓ т = 50d. (3. 31)
|
|
|
На участках гидродинамической и тепловой стабилизации потока теплоотдача по мере развития пограничных слоев уменьшается по длине трубы, число Нуссельта (Nu) уменьшается, асимптотически приближаясь к постоянному значению Nu∞ (рис. 3. 6). Это значение Nu∞ , называемое предельным, характеризует интенсивность теплоотдачи полностью стабилизировавшегося потока. В трубах длиной ℓ > > ℓ г и ℓ > > ℓ т среднюю теплоотдачу можно считать равной предельной Nu= Nu∞ .
Аналитическое решение задач при ламинарном и турбулентном стабилизированном течении связано с решением системы дифферен-циальных уравнений конвективного теплообмена (3. 10)-(3. 12). Однако строгое решение этих уравнений связано с большими математическими трудностями даже для ламинарного режима движения теплоносителя. Результаты достаточно высокой точности можно получить используя уравнения подобия для конвективного теплообмена.
При Re< 2300 и вязкостно-гравитационном режиме течения средний коэффициент теплоотдачи в прямых гладких трубах определяется по формуле:
Nuж = 0, 15Reж0, 33Prж0, 43 Grж0, 1(Prж/Prст)0, 25·ε ℓ . (3. 32)
Таким образом, зная величину Nuж, можно вычислить средний коэффициент теплоотдачи:
α = Nuж·λ /d. (3. 33)
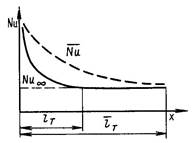
Рис. 3. 6. Изменение локального (Nuл) и среднего (Nu)
значения числа Нуссельта по длине трубы
За определяющую температуру принята средняя температура жидкости в трубе. Определяющий размер для круглых труб - внутрен-ний диаметр трубы, для каналов любого сечения – эквивалентный диа-метр
dэкв = 4F/P, (3. 34)
где F – площадь поперечного сечения канала (живое сечение потока);
P – смачиваемый периметр канала.
Например, для канала прямоугольного сечения а x b:
dэкв = 4аb/[2( а + b)] = 2аb/(а + b). (3. 35)
|
|
|
Множитель (Prж/Prст)0, 25 отражает влияние направления теплового потока, т. е. нагревается жидкость или охлаждается. При нагревании жидкости градиент температуры в пограничном слое больше, чем при охлаждении. Как показывает опыт и анализ влияния градиента температуры в случае нагревания и в случае охлаждения жидкости, коэффициент теплоотдачи при нагревании капельных жидкостей больше, чем при охлаждении. Следовательно, при нагревании жидкости множитель (Prж/Prст)0, 25 больше единицы, а при охлаждении – меньше единицы.
Поправочный коэффициент ε ℓ для коротких труб учитывает изменение среднего коэффициента теплоотдачи на нестабилизиро-ванном начальном участке потока (ℓ /d< 50) и зависит от отношения ℓ /d. Значения ε ℓ представлены в таблице 3. 1.
Таблица 3. 1. Значение ε ℓ при ламинарном режиме
| ℓ /d |
| ε ℓ | 1, 9 | 1, 7 | 1, 44 | 1, 28 | 1, 18 | 1, 13 | 1, 05 | 1, 02 | 1, 0 |
Для газов в широком диапазоне изменения температур Pr ≈ const. Поэтому для конкретных газов формулу (3. 32) можно упростить. Например, для воздуха она приводится к виду:
Nuж = 0, 13Reж0, 33Grж0, 1·ε ℓ . (3. 36)
При турбулентном режиме течения теплоносителя (Re≥ 104) благодаря интенсивному перемешиванию температура ядра потока практически остается постоянной. Основной градиент температуры относится к пограничному слою. Свободное движение не оказывает влияния на теплоотдачу при турбулентном режиме течения, и потому число Грасгофа не входит в уравнение подобия. Для расчета среднего по длине трубы коэффициента теплоотдачи при развитом турбулентном движении применяется следующая формула:
Nuж = 0, 021Reж0, 8Prж0, 43 (Prж/Prст)0, 25·ε ℓ . (3. 37)
Это уравнение справедливо при Reж = 104 – 5·106 и Prж = 0, 6 – 2500. Для воздуха и двухатомных газов формула (3. 37) принимает следующий вид:
Nuж = 0, 018Reж0, 8·ε ℓ . (3. 38)
Поправочный коэффициент ε ℓ для коротких труб с нестаби- лизированным течением (ℓ /d< 50) представлен в таблице 3. 2.
Из формулы (3. 38) получим:
α = (0, 018 λ w0, 8) / (ν 0, 8d0, 2). (3. 39)
Как следует из (3. 39) коэффициент теплоотдачи увеличивается с увели-чением скорости жидкости и с уменьшением диаметра трубы.
При движении теплоносителя в изогнутых трубах и змеевиках под действием центробежной силы возникает вторичная циркуляция, наличие которой приводит к увеличению коэффициента теплоотдачи. При уменьшении радиуса кривизны влияние центробежного эффекта увеличивается.
|
|
|
При движении жидкости в области развитой турбулентности коэффициент теплоотдачи для изогнутых труб α из определяется по фор-муле:
α из = ε D·α, (3. 40)
где α – коэффициент теплоотдачи в прямой трубе по формуле (3. 37).
Поправочный коэффициент ε D определяется по формуле:
ε D = 1+ 3, 6 (d/D), (3. 41)
где d – диаметр трубы;
D – диаметр спирали.
В змеевиках действие вторичной циркуляции распространяется на всю длину трубы.
Таблица 3. 2. Значение ε ℓ при турбулентном режиме
| Reж | ℓ /d |
| 1·104 | 1, 65 | 1, 50 | 1, 34 | 1, 23 | 1, 17 | 1, 13 | 1, 07 | 1, 03 |
| 2·104 | 1, 51 | 1, 40 | 1, 27 | 1, 18 | 1, 13 | 1, 10 | 1, 05 | 1, 02 |
| 5·104 | 1, 34 | 1, 27 | 1, 18 | 1, 13 | 1, 10 | 1, 08 | 1, 04 | 1, 02 |
| 1·105 | 1, 28 | 1, 22 | 1, 15 | 1, 10 | 1, 08 | 1, 06 | 1, 03 | 1, 02 |
| 1·106 | 1, 14 | 1, 11 | 1, 08 | 1, 05 | 1, 04 | 1, 03 | 1, 02 | 1, 01 |
В области переходного режима 2300< Re< 104 большое влияние на теплообмен оказывает, как и при ламинарном режиме движения, естественная конвекция, величину которой характеризует число Грасгофа. Так как в настоящее время не имеется удовлетворительных методик расчета теплоотдачи в переходной области, определение коэф-фициента теплоотдачи может быть произведено только приближенно с помощью следующего уравнения подобия:
Nuж = КоPrж0, 43 (Prж/Prст)0, 25·ε ℓ , (3. 42)
где К0 – коэффициент, зависящий от чисел Рейнольдса и Грасгофа
К0 = f (Reж·Grж). Значения этого коэффициента приведены в
таблице 3. 3.
ε ℓ - поправочный коэффициент для коротких труб, учитывающий изменение среднего коэффициента теплоотдачи на нестабилизиро-ванном начальном участке потока (ℓ /d< 50). Зависит от отношения ℓ /d. Значения ε ℓ представлены в таблице 3. 1.
Таблица 3. 3. Значение К0 при переходном режиме движения жидкости
| Re·10-3 | 2. 3 | 2, 4 | 2, 5 |
| K0 | 3, 3 | 3, 8 | 4, 4 | 6, 0 | 10, 3 | 15, 5 | 19, 5 | 27, 0 | 33, 3 |
3. 2. 2. ТЕПЛООТДАЧА ПРИ ПОПЕРЕЧНОМ
|
|
|


