 |
2. 3. Нестационарная теплопроводность
|
|
|
|
2. 3. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
2. 3. 1 ОСНОВНЫЕ ПОЛОЖЕНИЯ
Если температурное поле меняется во времени, то тепловые процессы, протекающие в таких условиях, называют нестационарными.
Нестационарные процессы теплопроводности так же широко распространены в технике, как и стационарные. Это процессы нагревания или охлаждения тел. В режиме нестационарной теплопро-водности работают, например, регенеративные воздухоподогреватели котельных установок, в которых одна и та же поверхность нагрева омывается то горячим, то холодным теплоносителем (дымовыми газами или воздухом). При протекании горячих дымовых газов тепло воспри-нимается стенками воздухоподогревателя и в них аккумулируется. При протекании холодного воздуха это аккумулированное тепло им воспри-нимается.
Другой пример – пропарочные камеры на заводах сборного железобетона, в которых для ускорения твердения бетона применяют его термовлажностную обработку, которая включает в себя периоды нагревания, изотермической выдержки (при максимальной температуре) и охлаждения.
Передачу теплоты при нестационарном режиме можно определить, если найти закон изменения температурного поля и теплового потока во времени и в пространстве:
Т = f (x, y, z, t) и Q = φ (x, y, z, t). (2. 52)
При оценке нестационарного режима теплообмена цель расчета состоит в определении температурного состояния тела и количества полученной или отданной телом теплоты по истечении определенного периода времени.
Зависимость температуры не только от координат, но и от времени затрудняет графическое изображение даже одномерного температур-ного поля. На рис. 2. 8, α показаны кривые изменения температуры тела в процессе его нагревания. При погружении тела в среду теплоносителя с постоянной температурой Тж сначала прогревается поверхность тела Тст, а спустя какое-то время начинает изменяться температура центра Тц. С увеличением времени прогрева температуры в теле выравниваются и при t → ∞ становятся равными температуре греющей жидкости. Характер изменения теплового потока, поступающего в тело при его нагревании, показан на рис. 2. 8, b. Тело перед нагревом имело однород-ное температурное поле.
|
|
|
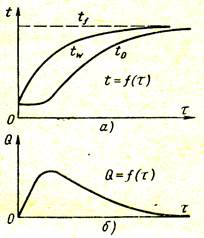
Рис. 2. 8. Зависимость температуры стенки и количества
передаваемого тепла от времени при нагревании
По мере прогрева тела количество воспринимаемой теплоты сначала резко увеличивается, достигает некоторого максимума, соответ-ствующего максимальной разности температур поверхности и центра, затем уменьшается и в пределе становится равной нулю. Площадь, ограниченная осью абсцисс и кривой Q= f (t), соответствует полному количеству теплоты, поступившему в тело за время t. Эта теплота аккумулируется телом и идет на повышение его энтальпии (теплосодержания).
Аналогичным образом протекает и процесс охлаждения тела, при этом его энтальпия уменьшается, а выделенная теплота передается в окружающую среду. На рис. 2. 9 показано температурное поле для всех точек (точнее, изотермических поверхностей) однородной плоской стенки при одинаковых условиях охлаждения обеих ее поверхностей. При таком изображении поля температурное состояние можно охарактеризовать только в определенные моменты времени t.

Рис. 2. 9. Температурное поле однородной плоской стенки при
одинаковых условиях охлаждения обеих ее поверхностей
Решение задачи нестационарной теплопроводности сводится к определению зависимости температуры и переданного количества теплоты от времени для любой точки тела. Однако такие решения могут быть получены при целом ряде упрощений и только для твердых тел простой формы – пластины, цилиндра и шара. Для практического использования эти решения обычно представляют в виде графиков.
|
|
|
Указанные зависимости могут быть найдены из решения дифференциального уравнения теплопроводности в твердом теле (без внутренних источников теплоты):
∂ Т/ ∂ t = α Ñ 2 Т. (2. 53)
Решение уравнения (2. 53) содержит постоянные интегрирования, для определения которых воспользуемся граничными условиями третьего рода, т. е. зададимся характером взаимодействия тела с окружающей средой
α (Тст– Тж) = - λ ст(∂ Т/ ∂ n)п=0, (2. 54)
где α – коэффициент теплоотдачи между жидкой (газообразной)
средой и поверхностью твердого тела;
Тст – температура поверхности стенки;
Тж - температура окружающей среды;
λ ст - коэффициент теплопроводности стенки;
(∂ Т/ ∂ n)п=0 - градиент температуры на поверхности стенки.
Физические параметры тела λ, с и ρ считаются постоянными, а начальное распределение температуры равномерным.
При одинаковой температуре во всех точках твердого тела, равной То, в начальный момент процесса теплообмена временные (начальные) условия имеют простой вид:
при t = 0 Т = То. (2. 55)
Решение уравнения (2. 53) с учетом граничных (2. 54) и временных (2. 55) условий дает уравнение температурного поля вида:
Т = f (α, λ, α , t, x, y, z, То, Тср, lо, l1, ..., ln). (2. 56)
Из уравнения (2. 56) видно, что температура зависит от большого числа переменных и постоянных параметров и решение его пред-ставляет весьма сложную математическую задачу. Подробное изложение решений имеется в специальных курсах по теплопередаче.
Анализ уравнения (2. 56) показал, что температуру твердого тела целесообразно представить в виде безразмерной избыточной температуры, а переменные и постоянные параметры сгруппировать в три безразмерных комплекса.
|
|
|
Обозначим избыточную температуру в любой точке тела в произвольный момент времени через θ:
θ = Т – Тж. (2. 57)
.
Для точек, расположенных на поверхности и в центре стенки (на оси цилиндра):
θ ст = Тст – Тж; θ ц = Тц – Тж. (2. 58)
Для начального момента времени:
θ о = То – Тж. (2. 59)
Тогда безразмерная избыточная температура:
θ /θ о = (Т – Тж) / (То – Тж). (2. 60)
Безразмерные комплексы:
Bi = α l/λ – число Био; (2. 61)
Fо = α t/l2 – число Фурье; (2. 62)
ξ /l - безразмерная координата;
ξ - координата (ξ = x – для стенки; ξ = r -для цилиндра);
l - характерный линейный размер тела (l = δ – для
стенки, толщина которой равна 2δ ; l = R – для цилиндра).
Числа Био и Фурье являются критериями теплового подобия (подроб-нее о теории подобия см. в разделе «Конвективный теплообмен»). Число Био представляет собой один из самых важных параметров теории теплопроводности. Им определяется характер соответствия между тем-пературными условиями в окружающей среде и распределением температуры в теле:
Bi = α /(λ /l).
Число Bi является количественной мерой интенсивности теплообмена между поверхностью тела и окружающей средой, оцениваемой по сравнению с проводимостью λ /l стенки.
|
|
|
Число Фурье является мерой скорости изменения температуры тела при неустановившемся тепловом состоянии:
Fо = α t/l2 = (λ /l)l2t / сρ l3.
Fo представляет собой отношение масштаба количества теплоты (λ /l)l2t, притекающей вследствие теплопроводности, к масштабу изменения теплосодержания тела сρ l3.
В результате решение дифференциального уравнения теплопровод-ности, описывающее нестационарное температурное поле в теле, имеет следующий вид:
n=∞
θ /θ о = ∑ A(μ n)U(μ n ξ /l)exp(-μ n2Fo), ( 2. 63)
n=1
где А и U - некоторые функции;
μ n – корни характеристического уравнения μ =μ (Bi).
Или в общем виде
θ /θ о = f ( Fo, Bi, ξ /l), (2. 64)
вид функции в котором зависит от формы тела.
|
|
|


